出口宽度b2与离心泵流量关系的数值模拟

李文霏　郭轶波

摘 要：离心泵叶轮的液体受叶轮旋转及表面曲率的影响，常出现脱流、回流及二次流等现象，一般来说是比较复杂的三维湍流流动。目前的离心泵叶轮的水力设计主要以一元理论及试验经验数据为主，一旦试验泵与设计工况有偏差，将很难定量给出修正值。该文结合叶轮机械内部流动的数值计算，通过保证扬程不变并同时改变叶轮出口宽度b2，揭示叶轮出口宽度与离心泵的定量关系，对后续离心泵出口宽度的修正提供一定的指导意义。

关键词：叶轮出口宽度 离心泵 数值计算 流量

中图分类号：TM62 文献标识码：A 文章编号：1674-098X（2015）06（a）-0094-03

离心泵的出口参数主要包括：叶轮外径D2、出口宽度b2、叶片出口安装角β2，这些出口几何参数与泵的性能曲线、效率及扬程相互影响。目前在泵的水力设计中，主要假设泵叶轮的流动是轴对称，则同一个过水断面上的轴面速度均匀分布，即利用一元理论以及大量试验统计数据进行离心泵叶片的水力设计，一旦泵的设计流量不满足要求，很难定量给出需修改的叶轮出口参数值。该文结合NUMECA FINE软件，以叶轮出口宽度值为变量，采用全三维的湍流模型进行数值计算，定量给出离心泵流量的变化规律。

1 叶轮出口宽度b2与流量关系的理论分析

根据文献[1]，出口宽度b2与流量Q的关系如下所示：

Q为流量；

D2为叶轮外径；

b2为叶轮出口宽度；

ηv为水泵水力效率；

ψ2为出口叶片的排挤系数；

V2r为流体出口速度的轴面速度。

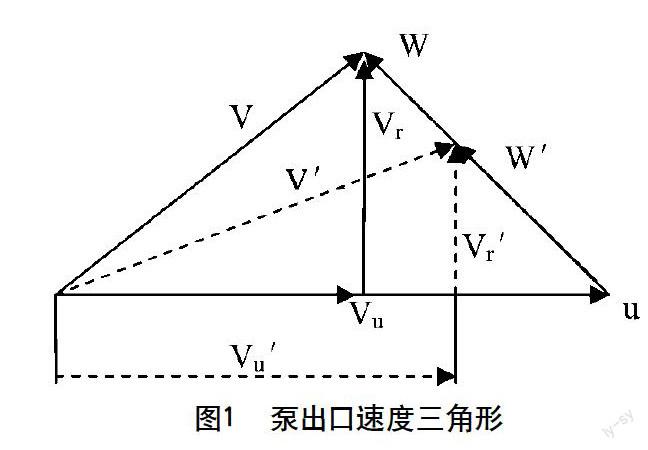
由上式可知，在保持扬程（图1的Vu不变）不变的情况下，当b2改变时，其与流量呈近似的线性关系。对于泵出口速度三角形，由于其出口速度不再受叶片约束，可认为出口的相对速度方向不变；当b2减小时，Vu′略有增大即泵扬程增加，Vr′减小即流量有所减小。

由以上理论分析可知：在保持扬程不变的情况下，减小泵出口宽度其流量也会减少，增大泵出口宽度其流量有所增加。

β2为叶片出口安装角；

θ为扬程特性曲线（HT∞—QT）的夹角；

若b2越大，则θ角越小，即HT∞—QT直线平坦，实际性能曲线越容易出现驼峰，故从消除驼峰角度来讲，出口宽度b2不宜过大。

2 叶轮出口宽度b2与流量关系的试验分析

由文献[2]可知，确保泵扬程保持不变的情况下，在移动前盖板改变b2（b2′>0.9b2范围内，b2′为窄叶轮的出口宽度）时，对大量数据进行统计分析后，得到原型泵的流量与窄叶轮的流量保持如下关系：

由文献[3]可知，通过给出整个系列28种规格的单级双吸性能曲线的相关数据，最后使用数据统计的方法，得到如下所示关系：

当b2′=（0.63-0.77b2）H时由以上试验结果可知，离心泵出口宽度b2在不同的范围时，其流量也呈现出不一样的统计关系。

3 离心泵叶片的结构设计

本文选定的原型泵设计参数为：流量Q=80 m3/h，扬程H=43m，转速n=2900 r/min。通过三维软件对该离心泵叶片进行三维建模，得到相关的几何结构参数如表1所示。

4 离心泵叶片的网格划分

NUMECA FINE采用多重网格划分技术，其主要思想是先在细网格上迭代，然后把数值结果传递到粗网格上；由于粗网格的网格少，计算时间少并可消除高频误差，则将更快的加速计算收敛。

根据NUMECA FINE技术手册，需要确定第一层网格的大小，其计算式如下所示：

ywall为壁面第一层网格大小，m；

Vref为参考速度，m/s；

Lref为参考长度，m；

ν为运动粘性，m2/s；

为无量纲量，不同的湍流模型，取不同的值。

在本文中，Lref取叶轮出口直径（0.194 m），Vref取叶轮出口的线速度（30 m/s），ν取1.01×10-6 m2/s，取值为6，最后计算得ywall为1.46×10-5。

在NUMECA FINE中，判定网格质量主要有3个指标：最小正交性应接近90°，最大长宽比接近1，最大延展比接近1。若网格质量远远小于此要求时，可通过调整展向网络数目、增加多重网格数或者调整网格光顺步数来改善网格质量。

5 边界条件的设定

该文为确保扬程不变的前提条件，进口采用总压及总温（Pts=1.01× 105Pa，Tt=293K）的边界条件，出口采用出口静压（Ps=4×105Pa）的控制方式，通过改变出口静压值，得到不同工况点的流量及扬程值，初场给定静压分布。

6 离心泵叶轮内部流动的求解及结果分析

该文中采用NUMECA FINE的商用软件包，使用时间推进法求解三维定常的雷诺平均纳维斯托克斯方程。紊流模型采用Spalart-Allmaras模型，該方程可模拟流动分离与转捩，对泵内流场的具有较好的模拟效果；为加速收敛，计算采用全多重网格及残差光顺方法，以获得较快的收敛速度。

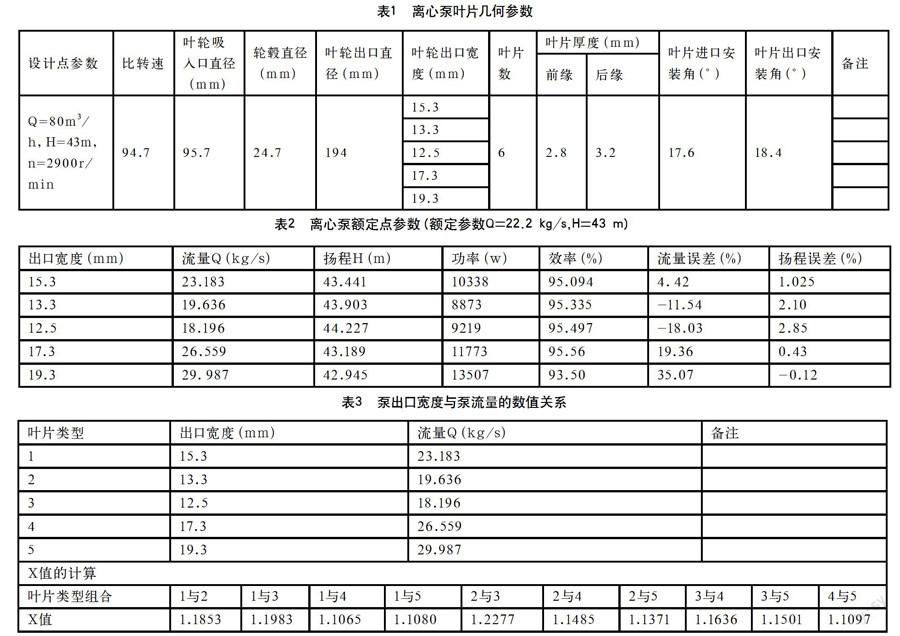
由NUMECA FINE的计算结果可知，在不同的出口宽度b2下，其流量、扬程、功率、效率的数值见表2。

由于此次仅对泵叶片作流场分析，即未考虑叶轮出口的突扩损失以及容积损失、回流影响以及机械损失，故数值计算的泵效率偏高。

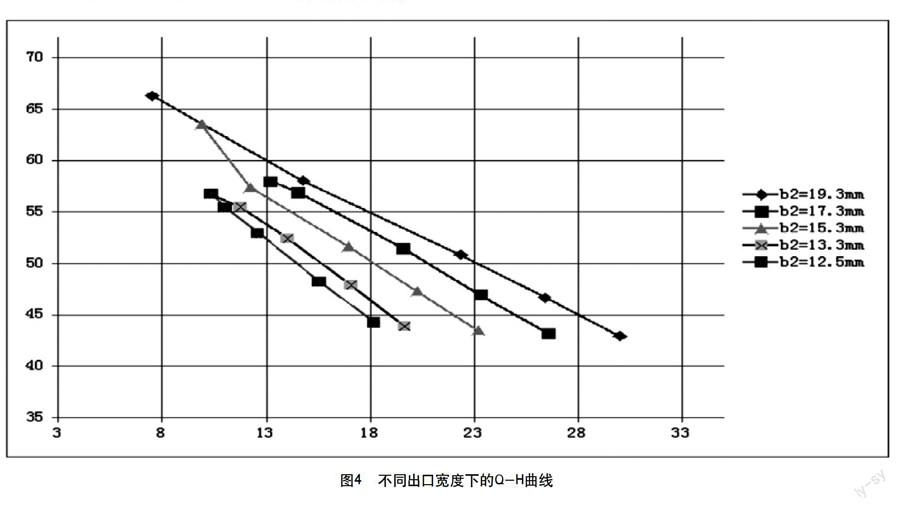
对于同一个泵出口宽度，选取5组不同的出口静压值，则不同泵出口宽度的Q-H流量曲线如图4所示。

由图4可知，随着泵出口宽度的增加，其Q-H曲线变得越平；由公式1-1可知，当b2越大则θ角越小，即Q-H曲线变得越平坦。此数值计算的结果与理论保持了较好的一致性。

另外，随着泵出口宽度的增加导致出口面积增大，在扬程不变的情况下，其流量也在呈增大趋势。此数据计算结果与理论保持了较好的一致性。

由表2的数据可知，对于相同的叶轮外径、进出口安放角、叶片数等均一致的情况下，叶轮仍然存在一个最佳出口宽度值（与结构设计流量误差值最小），此与试验的统计数据一致。由文献[1]可知，叶轮出口宽度的统计计算公式如下，代入数据得最佳泵出口宽度为11.99mm。

由图4的数据可知，当b2>b2′> 0.73b2，泵出口流量随着泵出口宽度的减小而减小；当1.26b2>b2′>b2，泵出口流量随着泵出口宽度增大而增大。此结论与理论分析及试验数据统计相符得较好。

7 结语

该文结合三维建模软件及CFD软件对泵出口宽度与流量之间的关系进行了定量分析，泵出口宽度与流量存在正相关关系并给出相应的数值关系式，其数值结果与理论设计及试验数据都有较好的吻合度，对后续泵的设计、修改均有一定的指导意义。相比于泵试验的试验设备昂贵、周期长等不足，数值计算成本低并可得到大量不同工况点的数据，随着计算机及数值计算方法的发展，流场的数值计算将会有更广阔的应用前景。

参考文献

[1] 关醒凡.现代泵技术手册[M].北京：宇航出版社，1995.

[2] 范宗霖，刘建军，王昕.改变叶轮出口宽度扩大离心泵性能范围[J].水泵技术，2004（2）：3-7.

[3] 上海KSB公司omega泵系列样本[Z].

[4] 杨华，谷传纲，王彤.时间推进法求解离心泵内部不可压流场[J].工程热物理学报，2005，26（1）：61-65.

[5] 孙自祥，吴玉林，薛敦松.离心泵叶轮内部紊流数值计算[J].工程热物理学报，1996（S1）：64-67.

[6] 邢白俊，王红哲.低比转速多级离心泵消除驼峰的试验研究[J].水泵技术，2001（6）：20-23.