推力调心滚子轴承设计方法探讨

郭　帅（洛阳LYC轴承有限公司技术中心,河南　洛阳　471039）

推力调心滚子轴承设计方法探讨

郭帅
（洛阳LYC轴承有限公司技术中心,河南洛阳471039）

摘要：本文侧重对调心滚子轴承方式进行了基础研究，并对设计过程中存在的问题与解决对策进行阐述。主要目的是为了能够完成对推力调心滚子轴承的技术优化。

关键词：推力轴承;调心滚子轴承;参数;设计

推力调心滚子轴承具有座圈滚道球面与轴承中心轴一致的点的球面，为此，应当具有自动调心能力。其在对轴度以及轴绕曲方面缺少敏感性的特征。调心滚子轴承本身具有在外圈以及轴承座壳提空不宜采用过盈配合的特征。对于调心滚子轴承的安装轴向游隙，可用轴颈上的调整螺母、调整垫片和轴承座孔内的螺纹，或用预紧弹簧等方法进行调整。本文针对推力调心滚子轴承设计方法进行了综合分析。

1　座圈设计部分

1.1座圈设计中的球面滚道以及非装配端面直径设计

假设球面滚道与非装配端面之间形成的直径为d2，其中，d2通过公式可以表示为：

d2=D-2Kd（D-d）

上文当中的Kd取值可以从下表当中进行选择：

表1

为此上式可以写成为D-d2=2Kd（D-d）

这其中的限制条件（a）当中Sw则可以通过公式SW=D-d2≥0.05

（D-d）来表示。

通过上式可以发现，当Kd值超过了0.025就可以达到限制性条件。

这也就是上式当中问题所在，为此，在进行设计的过程中可以适当将Kd的值控制在较大的范围当中即可。

1.2球面滚道以及内径d1之间的基准端面高度H2设计分析

假设上述内容当中的h2可以通过公式：

h2=Kh（D-d）

进行表示；

可上述式中的Kh需要通过表1进行取值，则这个时候在限制条件下h2≥0.05（D-d），通过这种方式不难发现，上式当中的Kh在取值的过程中只要能够超过0.05则就能够达到实际要求。这时候的，这也就是本文当中的主要问题。为此，在对Kh进行取值的过程中可以在0.05-0.07的范围中。

需要注意的是Kd以及Kh在进行取值的时候，无论其取值范围为多少，最终还是需要被限定在限制性条件当中，并基于此进行取值检验。

2　滚子设计

2.1接触角设计公式

接触角主要指的是滚子素线在于座圈滚道两者之间的接触点上的切线以及轴承轴心线方面产生的夹角：A=arctg(d2-d1)/(C-h2)

2.2接触角夹角β设计公式

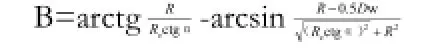
2.3滚子的端面之间产生的长度Lwe

滚子端面大小之间产生的长度通常情况下并不涵盖球形端面实际的高度情况，其在进行取值的过程中精度一般需要控制在0.001。

2.4滚子直径端面之间的距离取值与设计公式:L2=0.5Lwe-Rsinβ;L1=Lwe-L2

通过上述当中的设计公式可以发现，因为采用Lwe公式计算则取值能够缩减0～0.5左右，这种情况下L2在进行取值的时候则能够降低0～0.25，能够到轴圈最小壁厚。这个过程中因为L1本身同样会降低0～0.25。为此，Lwe需要在L1本身得到确定之后再进行设计。除此之外，滚子绝对不会存在滚子轴向放线上，并突出座圈滚道。为此，发生问题通常情况下会L1L2的设计方面，也就是在设计的过程中一定忽略了一些要素。

如在下图1当中，其中点A则表示的额是滚子圆弧素线产生弦长中点，其中B点则表示的额是接触点。也就是圆弧素线当中的中点位置。这当中的O2表示的而是左权滚道曲率中心，其中O3则表示的是滚子素线产生的曲率中心。

因为R、Lwe在取值上并不相同，两者之间的取值差异可能相差在几微米或者是几毫米之间。因此这种差异可以被忽略掉。同时，因为座圈在进行设计时候已经确定，滚子与座圈之间产生的接触点，以及滚子最大直径等的实际位置也已经设计完成，当轴圈也确定的情况下就能够对上述当中相关问题进行解决。

3　轴圈设计

轴圈总高度为h5,取值精度为0.5，滚道最小直径为d5，取值精度为0.001，具体表示为

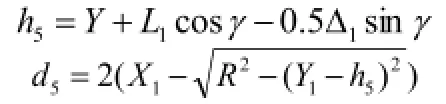
根据h5计算可知，滚子小端一定在轴圈滚道范围内。基于h5取值精度为0.5，若将0.5舍去将会出现滚子小端凸出轴圈滚道现象，若将0.5选择入而不舍去，将会避免出现这种现象。但与此同时若将0.5入，则会造成座圈径向壁厚变小，则无法实现对上述分析条件的满足。下面将基于此进行取值精度为0.1计算的设计对比分析。

4　设计计算实例综合分析

针对上述中内容进行讨论发现，一些细节性问题还是会影响到推力调心滚子轴承设计，其中294当中的设计计算在与原设计之间就存在对比差异性，这通过对比表2可以发现两者之间的区别情况。

表3

5　结语

综上所述，本文针对推力调心滚子轴承设计方法进行了简要分析，首先对座圈设计部分进行了阐释，并对座圈球面滚道与座圈非装配端面之间产生的直径、与高度等的设计公式进行了分析。同时，分析了滚子接触角以及相关要素内容，并在此基础上对轴圈完成了设计分析。通过上述中内容可以详尽了解调心滚子轴承的设计方法，希望能够通过本文对未来的工作开展提供一些帮助。

参考文献：

[1]李林位，高晓峰.风电机组主轴轴承疲劳寿命分析与数值模拟[J].洛阳轴承研究所,2013（23）：234-235.

[2]何慧华，盖得文.推力调心滚子轴承设计方法[Z].洛阳:洛阳轴承研究所,2013.