基于遗传算法的永磁同步电机PID控制器参数设计与仿真研究

黄亚菲（大连交通大学，辽宁　大连　116028）

基于遗传算法的永磁同步电机PID控制器参数设计与仿真研究

黄亚菲
（大连交通大学，辽宁大连116028）

摘要：永磁同步电机属于非线性、时变、强耦合的复杂控制系统，采用常规PID控制器设计方法不能获得良好的控制品质(包括稳定性、快速性、鲁棒性)。遗传算法属于智能优化算法的一种，具有良好的全局寻优能力、不易陷入局部最优解、并行性好等优点，因此，本文采用遗传算法来实现PMSM交流伺服系统的PID控制器参数整定。通过MatLab/Simulink仿真得到，本文所提方法具有良好的控制品质。

关键词：PID控制器；遗传算法；交流伺服系统

0　引言

永磁同步电机具有体积小、重量轻、效率高、结构简单和损耗小等优点，与直流电动机相比，永磁同步电机没有换向器和电刷的缺点；和感应电机相比，不需要无功励磁电流，因而它的效率和功率因数高，力矩的转动惯量比较大，定子电流和定子绕组减小，控制性能好。永磁同步电机的矢量控制系统能够实现高精度，大范围调速和定位控制，因此引起了国内外专家和学者的广泛关注[1]。永磁同步电机控制系统主要由永磁同步电机（PMSM）、电流传感器，PWM逆变器、速度传感器、位置传感器、电流控制器等部分构成。如图1所示：

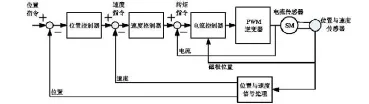
图1　PMSM控制系统方框图

1　遗传算法

遗传算法(GeneticAlgorithm，简称GA)是在达尔文进化理论与孟德尔学说基础上兴起的，通过模仿生物进化过程发展而来的全局搜索与优化算法[2]。GA算法具有并行、高效及全局搜索能力并且能在搜索过程中获取和积累搜索经验，最终求得最优解。遗传算法的基本思路：根据待寻优问题的目标函数，构造一个适应度函数。然后生成初始种群，对种群进行评价、交叉、变异、选择等操作。通过数次进化，得到适应度最高的个体作为问题的最优解。

2　基于遗传算法整定PMSM控制系统PID控制器参数的设计过程

Step1:编码

遗传算法的初始种群是通过编码来产生的，比较常用的编码方式有两种，二进制编码和浮点数编码。而二进制编码是目前使用最多的编码方式，其思想是首先假设某一参数取值范围为[Xmin～Xmax]，若采用长度为L的二进制串来表示，那Xmin表示000...000，Xmax表示111….111。二进制编码方法的精度为：

二进制编码具有简单、有利于交叉变异操作，但此编码方式不能够反映参数的实际特性。对于待寻优的较大参数需要很长的二进制数表达，导致系统搜索空间增大。本文采用遗传算法对PMSM控制系统PID参数整定中，由于参数较大，因此二进制编码不太合适本文的遗传算法，本文采用浮点数编码方式。

浮点数编码与十进制编码相似，用一个特定范围内的浮点数来表示每个个体的基因值。需要寻优的PID控制器三个参数就是编码的长度，十进制编码适合在遗传算法中表示范围较大的数，适合PID控制器参数的编码且不需要译码环节。因此，本文选择浮点数编码（十进制编码）方法编码。

Step2:适应度函数

适应度函数是衡量个体或解的优差性的评判函数，根据问题的种类不同，适应度函数的定义方式也千差万别。遗传算法中每个个体均对应一个适应度函数，也称为目标函数。遗传算法的寻优效果取决于适应度函数的好坏。通常PMSM控制系统中PID控制器参数整定时测试信号选用单位阶跃信号。为了使控制系统具有优越的动静态控制品质，本文采用以下公式作为遗传算法的目标函数：

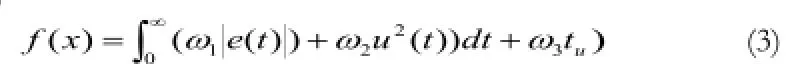
Step3:复制

复制操作中需要考虑相对适应度的概念，如式(5)所示：

如上式所示，相对适应度的值pi越大，被保留下来的概率就越大；为了避免“早熟”现象，pi较小的值也存在被保留下来的可能，本文首先按照公式(5)计算出每个个体的适应度值，然后根据式子（6）统计出各个个体的累积概率Qi，接着随机产生一个0到1之间的随机数r，若Qr-1＜r＜Qi，则个体i被复制进入下一代新种群。重复以上步骤，直到下一代的群体规模与上一代群体规模数量达到相同。

Step4:交叉

在浮点数编码方式的过程中，交叉操作和变异操作都需要在各基因的交界处进行。本文浮点数采用的编码长度为3，因此产生两个交叉点，随机地选取1到2个基因进行交叉产生新的个体种群。

Step5:变异

本文采用均匀变异方法进行遗传算法的变异操作，其具体操作是：首先设置系统的变异概率pm，然后随机的产生0到1之间的浮点数，对个体的每个基因个体进行遍历操作，若r＜pm，则将遍历到的基于浮点数编码的基因重新编码，产生新的基因和个体。

3　基于遗传算法的PMSM控制系统的PID参数整定仿真研究

采用Matlab/Simulink模型对控制系统PID控制器参数进行寻优，遗传算法参数和系统参数的设定如下表1所示。

表1　仿真系统参数的取值范围

在Matlab/simulink平台下仿真得到系统目标函数的优化曲线图和PMSM交流控制电机的速度单位阶跃曲线分别如图2、3所示。最终得到的PID控制器参数：SKP=21672,SKi=1.65,SKd=0.87, IKP=1200,IKd=0.56。

从图2、3可以看出基于遗传算法整定的PMSM交流控制系统的PID控制器参数是行之有效的。虽然存在一定的稳态误差，其总体控制品质符合永磁同步电机调速系统对速度的控制要求。

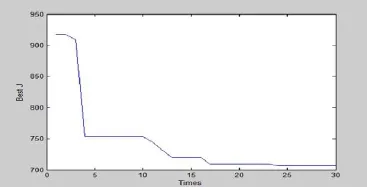
图2　目标函数优化曲线图

图3　系统闭环单位阶跃曲线图

4　结论

本文基于PMSM交流控制系统的控制器PID参数设计问题，采用遗传算法对PMSM的电流环、速度环PID进行参数整定。在Matlab/ Simulink平台下进行仿真分析，仿真结果表明基于遗传算法的PMSM系统PID控制器参数整定方法是行之有效的，PID控制器参数整定结果符合PMSM控制系统的动静态性能指标要求。

参考文献：

[1] 张建民，王俊科.永磁同步电机的模糊混沌神经网络建模[J].中国电机工程学报，2007,27(3).7-11.

[2]Smai1F,IbrahimA,Mar t inHR.Ident i f i cat ion of fat igue e raeks vi brat ion t es t ing[J].Journa l o f Sound and Vibration,1990,140:305-317.