基于容积卡尔曼的粒子PHD多目标跟踪算法
王海环,王 俊
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)
基于容积卡尔曼的粒子PHD多目标跟踪算法
王海环,王 俊
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)
标准粒子概率假设密度(standard particle probability hypothesis density,SP-PHD)滤波在预测粒子状态时没有考虑最新的观测信息,因而存在估计精度较低、粒子退化严重的问题,针对上述问题,提出基于容积卡尔曼的粒子概率假设密度(cubature Kalman particle probability hypothesis density,CP-PHD)滤波算法,该算法基于球面-径向容积数值积分准则,利用容积卡尔曼滤波(cubature Kalman filter,CKF)产生建议密度函数,并对其进行采样得到当前时刻的粒子状态,从而使粒子分布更接近于真实的多目标后验概率密度函数。同时,CP-PHD算法性能不受目标状态维数影响,与无迹卡尔曼粒子概率假设密度(unscented Kalman particle probability hypothesis density,UP-PHD)滤波相比,具有更强适应性和更好的跟踪性能。实验结果表明,CP-PHD算法的跟踪精度优于SP-PHD和UP-PHD。
多目标跟踪;粒子概率假设密度滤波;容积卡尔曼滤波;建议密度函数
0 引 言
为避免传统多目标跟踪算法中的数据关联,文献[1]基于随机有限集理论提出了概率假设密度(probability hypothesis density,PHD)滤波,该方法将目标的状态和观测量看成随机有限集,将单目标的Bayes估计推广到多目标跟踪中,通过传递多目标全局后验概率密度的一阶矩得到各目标的状态估计。由于PHD滤波算法不需要进行数据关联,这不仅降低了多目标跟踪中的计算量,同时也最大程度地保持了信息的完整性,因而受到越来越多的重视。
虽然PHD滤波算法只传递多目标全局后验概率密度的一阶矩,但在其递推过程中仍需要求解高维积分,通常情况下很难得到闭合解。解决上述问题的方法一般有两种:高斯混合概率假设密度[2](Gaussian mixture PHD,GMPHD)和粒子概率假设密度[34](particle PHD,P-PHD)。GMPHD是将目标的状态分布表示成多个高斯分量的加权和的形式,在线性高斯的条件下得出PHDF的闭合解。P-PHD又称为序贯蒙特卡罗概率假设密度(sequential Monte CarloPHD,SMC-PHD),是用一系列随机样本来近似多目标全局后验概率密度的一阶矩,具有粒子滤波的优点,能适用于非线性非高斯环境。
标准的粒子概率假设密度(standard particle probability hypothesis density,SP-PHD)滤波算法在预测粒子状态时,仅将目标状态转移方程作为建议密度函数,没有利用观测量,这会在目标运动模型不准的情况下,使大量粒子偏离真实目标状态,更新这些粒子的权值需要消耗大量计算,但经过若干步迭代后,这些粒子的权值会变得很小,对后验概率却几乎没有贡献,这就是粒子退化问题。针对上述问题,很多学者采用不同的建议密度函数,提出多种改进的P-PHD滤波算法,例如基于辅助粒子滤波的概率假设密度(auxiliary particle PHD,AP-PHD)算法[5]、扩展卡尔曼粒子概率假设密度(extended Kalman particle PHD,EP-PHD)滤波[6]、无迹卡尔曼粒子概率假设密度(unscented Kalman particle PHD,UP-PHD)滤波[7]等,这些算法都是利用观测值产生建议密度函数,从而达到修正粒子状态的目的,在一定条件下比SP-PHD算法精度高。但是AP-PHD通过二次采样产生建议密度函数,在增加算法计算量的同时,对算法的性能提升并不明显;EP-PHD采用扩展卡尔曼滤波(extended Kalman filter,EKF)产生建议密度函数,EKF对泰勒展开式高阶项的截断导致算法在非线性程度比较高时误差较大;UP-PHD采用无迹卡尔曼滤波[8](unscented Kalman filter,UKF)产生建议密度函数,UKF算法理论基础薄弱且当产生的sigma点的权值为负时算法不稳定。
容积卡尔曼滤波[9](cubature Kalman filter,CKF)是基于球面-径向容积准则,采用一系列容积点近似目标后验概率密度一种方法,属于利用数值积分解决高维积分问题的范畴。该算法理论性强,在非线性条件下性能优于EKF和UKF,实现中采用的容积点个数较UKF少,且算法稳定性好。鉴于以上优势,本文提出一种基于容积卡尔曼的粒子概率假设密度(cubature Kalman particle PHD,CP-PHD)算法,该算法采用容积卡尔曼产生建议密度函数,并对其采样得到粒子的预测状态。仿真表明,本文提出的算法其跟踪性能优于SP-PHD滤波算法和UP-PHD滤波算法。
1 概率假设密度滤波
经典的Bayes滤波理论适用于单目标跟踪,其思想是利用目标状态转移方程和观测方程,经过时间更新和量测更新两个步骤,实现对当前时刻目标状态的预测和修正。在多目标跟踪中,目标的状态、个数及观测量的数目都是时变的,为将经典Bayes理论推广到多目标跟踪中,文献[10]提出了随机有限集(random finite sets,RFS)理论,在此基础上建立多目标状态和观测模型。
状态模型表示为

观测模型表示为

式中,Xk={x1,x2,…,xn(k)}为k时刻目标的状态集,其中xi(i=1,2,…,n(k))为单目标状态矢量;n(k)是k时刻目标的个数;Zk={z1,z2,…,zm(k)}为k时刻目标的量测集,zi(i=1,2,…,m(k))为单个量测矢量;m(k)为k时刻观测到的量测的个数;Ek|k-1为存活目标状态集;Bk|k-1为衍生目标状态集;Ψk为新生目标的状态集;I(·)为目标量测集;Ck为杂波集。
基于以上模型,可推出多目标的Bayes估计递推式如下:
(1)预测

(2)更新

式中,gk(·|·)为多目标联合似然函数;pk|k(Xk|Z1:k)为多目标联合后验概率密度;pk|k-1(Xk|Z1:k-1)为多目标联合先验概率密度;pk|k-1(Xk|Xk-1)为多目标状态转移概率密度函数。
为解决多目标Bayes估计中集合积分的问题,Mahler提出利用多目标全局后验概率密度一阶矩(称为PHD或强度函数)代替其本身在Bayes递推式中传递,这就是PHD滤波器。已知k-1时刻的多目标一阶矩Dk-1(·),PHD滤波器的递推方程如下[1]:
(1)预测
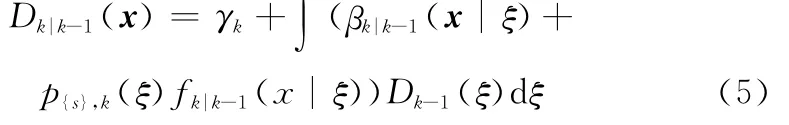
(2)更新

式中,ps,k(x)为目标存活概率;fk|k-1(·|·)为其单目标的状态转移密度;βk|k-1(·|·)为衍生目标的概率密度函数;γk为k时刻新生目标的强度函数;pd,k为k时刻目标检测概率;ck为杂波概率密度;λk为杂波平均数;gk(·|·)为单目标似然函数。
2 P-PHD滤波
尽管采用了全局后验概率密度的一阶矩近似,PHD的递推方程中仍需要计算高维积分,通常情况下难以得到闭合解。为解决这一问题,文献[3]提出采用粒子滤波实现PHD算法,这就是P-PHD滤波。P-PHD滤波是用一系列的加权粒子来表示全局后验概率密度的一阶矩在目标状态空间中的分布,通过对这些粒子的状态和权值进行繁衍和递推,便可得到对全局后验概率密度一阶矩的递推描述。
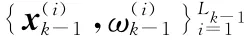
步骤1 预测
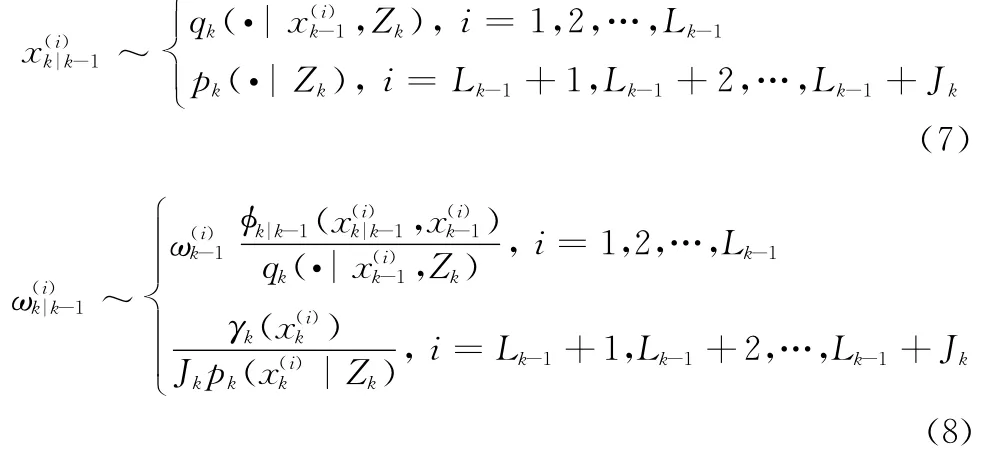
步骤2 更新
k时刻的量测集为Zk,用其对预测的粒子的权值进行更新得
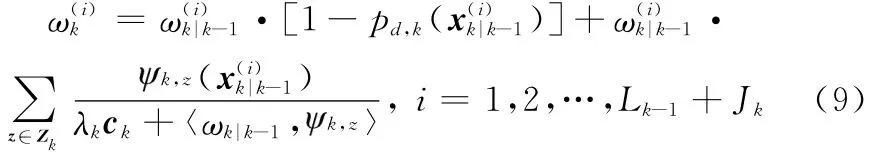
式中
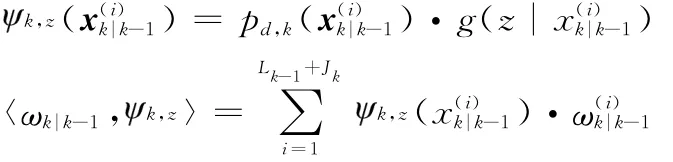
步骤3 重采样
步骤4 目标状态提取
利用k-means聚类方法得到目标状态估计的具体流程如下:
(2)重复步骤3和步骤4直到每个聚类不再发生变化为止;
(3)计算其他粒子与聚类中心的距离,并将它们分配给与其相距最近的聚类中心所代表的聚类中;
(4)计算每个新聚类的聚类中心(该聚类中所有粒子状态的均值);
(5)将最终得到的聚类中心作为目标状态估计输出。
3 CP-PHD滤波
同PF相似,在P-PHD滤波中,建议密度函数的选取对算法的性能至关重要。SP-PHD算法直接将目标状态转移方程作为建议密度函数,没有考虑当前观测信息,在多次迭代后容易出现粒子退化。考虑到状态转移方程和观测方程都有可能是非线性的,通常采用二次采样、EKF或UKF产生建议采样函数,但二次采样对算法性能提升不大,EKF在非线性程度较高时误差较大,UKF的性能优于二次采样和EKF[11-12],但在目标状态维数较多时算法性能不稳定。针对上述问题,本文提出利用CKF产生建议密度函数,该算法使用基于球面-径向容积准则的数值积分方法直接计算粒子的均值和方差,较之EKF和UKF,其精度更高,算法更稳定。
3.1 容积卡尔曼滤波
为得到非线性系统下Bayes滤波的递推式,文献[9]提出在高斯假设(系统状态和噪声都是高斯分布)的条件下,非线性滤波的问题可转化成求解被积函数为非线性函数×高斯概率密度的积分的问题。考虑最简单的形式

式中,f(·)为为非线性函数;x∈Rn,n为x的维度;I为n×n阶单位阵。
CKF通过以下两步求解式(10)形式的积分:
步骤1 将式(10)由直角坐标系转换到球面-径向坐标系下。令x=r y(yyT=1),则xTx=r2,r∈[0,∞),进而式(10)在球面-径向坐标系下的形式为

式中,Un表示单位超球面;σ(·)表示积分微元。式(11)进一步化简可写为

由式(12)可看出,直角坐标系下的多维积分可分解为径向一维积分和超球面多维积分的乘积。
步骤2 对式(12)通过高斯-厄米特准则和三次幂球面-径向准则进行数值近似求解,可得到


可以看出,CKF与UKF结构类似,但CKF所需的采样点的权值相同,选择较UKF简单,且采样点个数少于UKF。另外,UKF的采样点和权值依赖于参数,而参数的选择主要依靠经验,没有明确的理论基础,而CKF有严格的理论证明,且采样点和权值不依赖于参数,较UKF有更强的适应性。
3.2 CP-PHD滤波
CP-PHD滤波算法的框架与SP-PHD、UP-PHD相似,其主要区别为预测阶段建议密度函数的产生方法上。设目标的状态方程和观测方程为
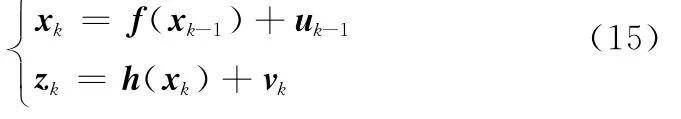
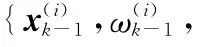
步骤1 预测
步骤1.1 对每一个粒子利用CKF产生建议密度函数
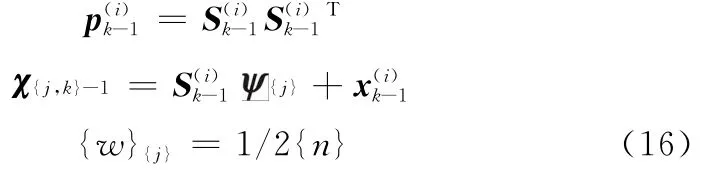
式中,n为目标状态的维度。
a.时间更新
根据观测方程传递容积点,更新粒子状态,并计算其协方差矩阵

b.量测更新
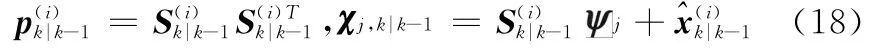
计算容积点所对应的观测量及其均值为


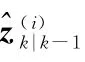

步骤1.2 通过采样获得粒子预测状态,并计算粒子权值。

式中,Jk=,ρ为每个新生目标的采样点数为新生目标的期望数。根据式(8)计算各个粒子的权值
步骤2 更新
该步骤与P-PHD滤波中的更新步骤相同,经过该步骤后得到更新后的粒子权值。
步骤3 重采样
步骤4 目标状态提取
该步骤与P-PHD滤波中的目标状态提取步骤相同。
3.3 性能分析
通过分析CP-PHD与UP-PHD的算法稳定性来比较两种算法的性能。CP-PHD与UP-PHD的主要不同点在于建议密度函数的产生方法不同:前者采用CKF,后者采用UKF。CKF和UKF都是利用数值积分来近似高维积分,定义稳定因子为

式中,i为数值近似中的采样点数。由文献[9]可知,当I>1时,多维积分的数值估计将引入较大误差。在UKF中,w0=κ/(n+κ),wi=1/2(n+κ)(i=1,2,…,2n),其中n+κ=3。当目标状态维数n小于等于3时,UKF和CKF的稳定因子都等于1,两者性能相当;当目标状态维数n大于3时,UKF的稳定因子大于1且随着目标维数的增加而增大,从而导致积分估计精度变差,而CKF的稳定因子与目标状态维数无关,始终为1。通过以上分析可知,在高维目标状态的条件下,CP-PHD的性能要优于UP-PHD。
4 实验仿真
本文在外辐射源雷达背景下,采用SP-PHD、UP-PHD、CP-PHD 3种方法对杂波环境下数目时变的多个目标进行跟踪。外辐射源雷达本身没有发射源,通过接收目标对第3方照射源的反射来实现目标探测。为提高定位和跟踪精度,外辐射源雷达通常采用多站联合定位,本文仿真采用3发单收(3个发射站,1个接收站)体制,如图1所示。

图1 3发单收外辐射源雷达示意图
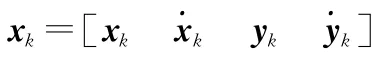
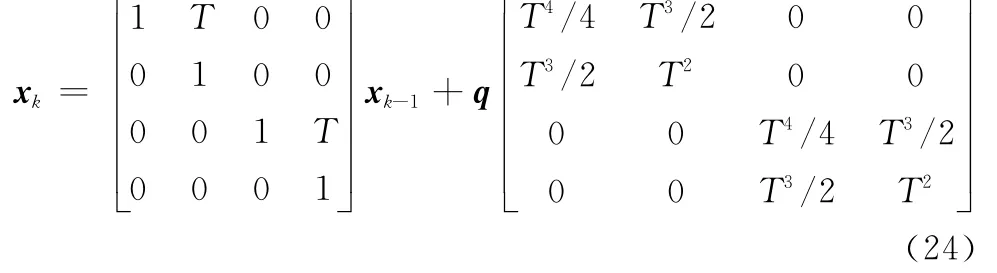
式中,q=3 m/s2为过程噪声标准差。观测方程为
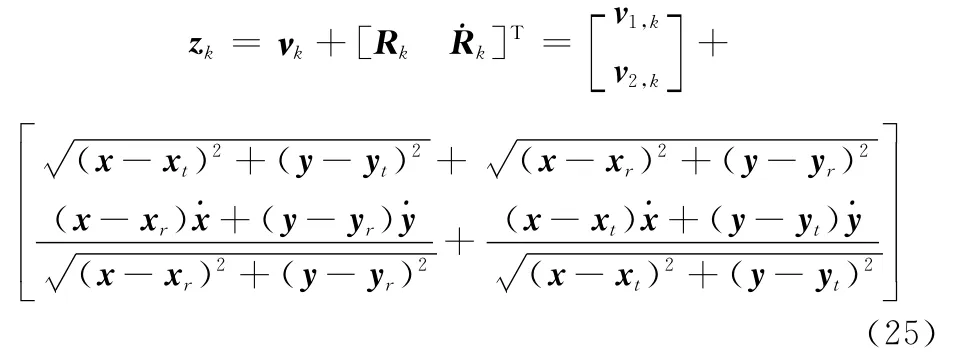
式中,νk为观测噪声;v1,k,v2,k为均值为零,标准差分别为100 m和1 m/s的高斯白噪声。设目标存活概率ps=0.98,检测概率pd=1,杂波在观测区域内均匀分布,杂波平均数λ=10,每个存活目标采样1 000个粒子,每个新生目标采样500个粒子。
目标真实轨迹与3种方法的跟踪轨迹如图2所示,由图2可直观地看出,SP-PHD算法出现错跟、漏跟的概率最大,这是由于SP-PHD在预测粒子状态时没有利用观测信息,预测粒子状态离真实值偏差较大,更新后较多粒子的权值很小,对得到目标当前状态贡献微弱导致的。UP-PHD算法和CP-PHD算法在预测粒子状态时利用了观测信息,因而其性能较SP-PHD算法有较大改善,其中CP-PHD的跟踪精度又优于UP-PHD算法,在3种算法中性能最优。
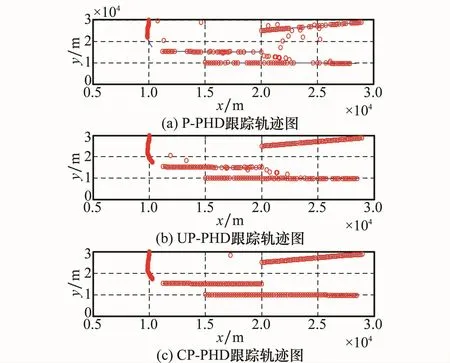
图2 跟踪轨迹图
文中采用最优子模式分配(optimal subpattern assignment,OSPA)标准[13]计算多目标跟踪中的误差,OSPA距离是单个目标的平均误差,由位置误差和势(目标个数)误差两部分组成,仿真中取距离误差敏感参数p=2,势误差敏感参数c=500,图3和图4分别为100次蒙特卡罗实验后,3种方法的目标数估计误差对比图和OSPA误差对比图。由图3、图4可以看出,SP-PHD的跟踪精度最差,UPPHD和CP-PHD的性能与SP-PHD性能相比都有很大改善,而CP-PHD的跟踪性能比UP-PHD更好,这符合第3.3节中对两种算法性能的理论分析。

图3 目标数目估计误差对比图
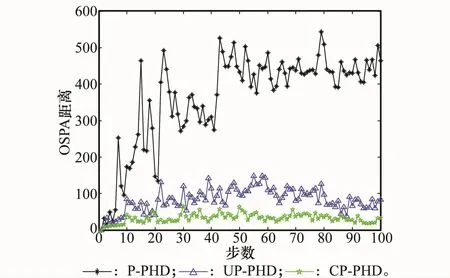
图4 OSPA误差对比图
改变杂波平均数,使λ=0.001,1,5,10,15,20,30,经过100次蒙特卡罗实验后,3种方法在不同杂波密度下的平均目标数估计误差对比图和平均OSPA误差对比图如图5和图6所示。由图5和图6可以看出,在相同杂波密度下,CP-PHD的算法性能要优于其他两种算法,同时随着杂波密度的增大,3种算法性能在逐步下降,其中SP-PHD的性能下能最快,而CP-PHD对杂波环境的适应性最强。
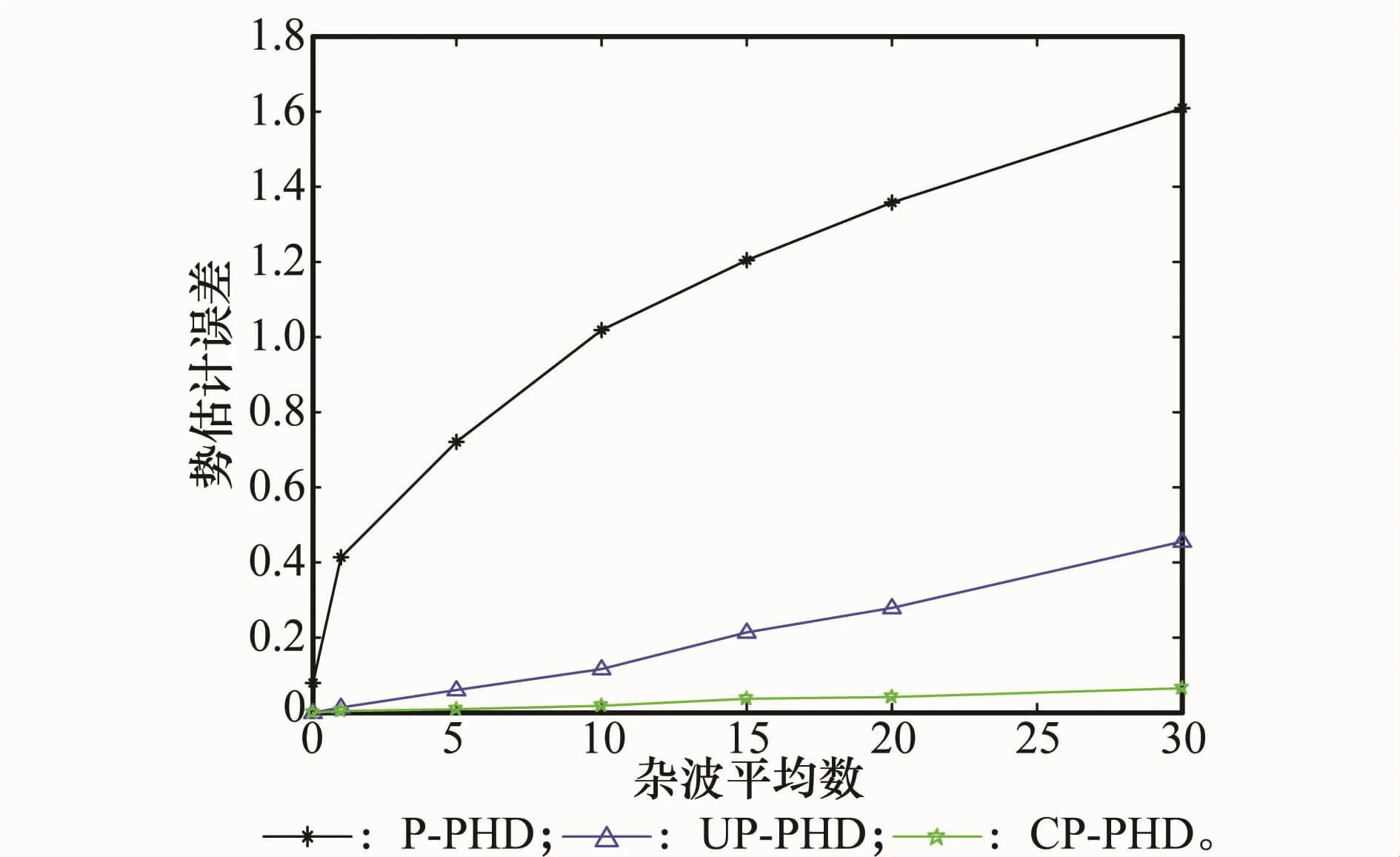
图5 目标数目估计误差图

图6 OSPA误差对比图
5 结 论
SP-PHD将目标状态方程作为建议密度函数,没有考虑当前观测信息,因而加剧了粒子退化。UP-PHD算法利用UKF产生重要性函数,提高了P-PHD的算法性能。但UKF算法中的参数依赖经验调整,没有明确理论依据,且算法的稳定性不高。本文提出的CP-PHD算法,通过CKF产生建议密度函数,由于CKF比UKF所需的样本点少,且算法性能不依赖于参数的设定,操作更简单,因此CP-PHD算法与UP-PHD相比,算法计算量较小,且适用性更强。通过仿真对比可以看出,CP-PHD的算法性能要优于UP-PHD算法。由于CKF中需要分解协方差矩阵,为避免这一操作,进一步增强算法的适用性和跟踪精度,有学者提出平方根CKF[9](square-rooted CKF,SCKF)算法和迭代的SCKF算法[1415],将SCKF算法和迭代SCKF算法与P-PHD算法相结合,在保证跟踪精度的同时提高算法稳定性是下一步的工作重点。
[1]Mahler R.Multitarget Bayes filtering via first-order multitarget moments[J].IEEE Trans.on Aerospace and Electronic Systems,2003,39(4):1152-1178.
[2]Vo B N,Ma W K.The Gaussian mixture probability hypothesis density filter[J].IEEE Trans.on Signal Processing,2006,54(11):4091-4104.
[3]Vo B N,Singh S,Doucet A.Sequential Monte Carlo methods for multi-target filtering with random finite sets[J].IEEE Trans.on Aerospace and Electronic Systems,2005,41(4):1224-1245.
[4]Zajic T,Mahler R.A particle-systems implementation of the PHD multitarget tracking filter[C]∥Proc.of the SPIE-the International Society for Optical Engineering,2003:291-299.
[5]Whiteley N,Singh S,Godsill S.Auxiliary particle implementation of probability hypothesis density filter[J].IEEE Trans.on Aerospace and Electronic Systems,2010,46(3):1437-1454.
[6]Melzi M,Ouldali A,Messaoudi Z.Multiple target tracking using the extended Kalman particle probability hypothesis filter[C]∥Proc.of the 18th European Signal Processing Conference,2010:1821-1825.
[7]Melzi M,Ouldali A.Multiple target tracking and classification using the unscented probability hypothesis density filter[C]∥Proc.of the 7th International Workshop on Systems,Signal Processing and their Applications,2011:4-21.
[8]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proc.of the IEEE,2004,92(3):402-422.
[9]Arasaratnam I,Hykin S.Cubature Kalman filter[J].IEEE Trans.on Automatic Control,2009,54(6):1254-1269.
[10]Mahler R.Multitarget detection and acquisition:a unified approach[C]∥Proc.of the SPIE International Society for Optical Engineering,1999:218-229.
[11]Zuo J Y,Jia Y N.Adaptive iterated particle filter[J].Electro-nics Letters,2013,49(12):556-557.
[12]Pathuri B V,Unterrieder C,Huemer M.Battery internal state estimation:a comparative study of non-linear state estimation algorithms[C]∥Proc.of the IEEE Vehicle Power and Propulsion Conference(VPPC),2013:1-6.
[13]Schuhmacher D,Vo B T,Vo B N.A consistent metric for performance evaluation of multi-object filters[J].IEEE Trans.on Signal Processing,2008,56(8):3447-3457.
[14]Mu J,Cai Y L,Zhang J M.Cubature particle filter and its application[J].Journal of Xi'an Jiaotong University,2011,45(8):13-17.(穆静,蔡远利.容积粒子滤波算法及其应用[J].西安交通大学学报,2011,45(8):13-17.)
[15]Wang H J,Jing Z R,Zheng W Q.Iterated cubature Kalman particle filter[J].Journal of Southeast University,2013,43(S1):85-88.(王华剑,景占荣,郑文泉.迭代容积卡尔曼粒子滤波算法[J].东南大学学报,2013,43(S1):85-88.)
Multitarget tracking with the cubature Kalman particle probability hypothesis density filter
WANG Hai-huan,WANG Jun
(National Lab of Radar Signal Processing,Xidian University,Xi'an 710071,China)
A cubature Kalman particle probability hypothesis density(CP-PHD)filter is proposed to solve the problems of the low state estimation accuracy and the serious particles degradation in standard particle probability hypothesis density(SP-PHD)filter because of unused the most recent observation.CP-PHD uses cubature Kalman filter based on spherical-radial cubature rule to generate the proposal density function and obtains the present particles states by sampling from the proposal density function,so that particle distribution is closer to the real multi-target posterior probability density function.Otherwise,the performance of CP-PHD is not affected by the dimension of target state,so CP-PHD has stronger adaptive and better tracking performance than unscented Kalman particle probability hypothesis density(UP-PHD)filter.Simulation results show that the tracking accuracy of CP-PHD algorithm is superior to SP-PHD and UP-PHD.
multitarget tracking;particle probability hypothesis density(PHD)filter;cubature Kalman filter(CKF);proposal density function
TN 953 文献标志码:A DOI:10.3969/j.issn.1001-506X.2015.09.02
王海环(1987-),女,博士研究生,主要研究方向为外辐射源雷达中的多目标跟踪。
E-mail:haihuanwang@126.com
王 俊(1969-),男,教授,博士,主要研究方向为无源多双基地雷达探测系统技术、雷达信号处理和数据处理。
E-mail:wangjun@xidian.edu.cn
1001-506X(2015)09-1960-07
2014-09-16;
2015-03-15;网络优先出版日期:2015-04-07。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150407.1321.004.html
教育部创新团队计划(IRT0954)资助课题

