基于SVM理论的大坝变形监测模型改进方法研究
杜传阳 郑东健
(1.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098;2.河海大学 水利水电学院,南京
210098)
大坝的安全运行关乎人民生命财产安全,其变形情况能够比较直接客观地反映出大坝运行状况,因此,建立有效的安全监测模型并及时分析和处理实测资料,发现异常及时处理,对大坝健康稳定运行至关重要[1-2].目前,根据研究进展及现状,常用的有支持向量机(Support Vector Machines,SVM)、统计模型、时间序列模型、神经网络等模型,这些模型各有利弊[3].其中SVM模型在大坝安全监测中应用广泛,适用于处理一些高维数、非线性的问题,且有良好的泛化能力[4],惩罚因子c和核参数σ的选择对模型性能有较大影响.本文在SVM理论的基础上对模型加以改进,并对各改进方法进行比较.利用粒子群算法(Particle Swarm Optimization,PSO)对SVM 模型的参数进行寻优,以提高预测效果.同时考虑到PSO算法容易陷入局部最优,引入速度因子和位置因子对标准PSO算法进行改进,一旦发现粒子存在陷入局部最优的趋势,则立即对粒子的位置进行初始化,称改进算法为自适应位置PSO(Adaptive Position PSO,APPSO)算法[5];同时,马尔科夫链模型具有适用于数据波动较大的特点,可以用来克服由于实测数据波动较大影响拟合和预报精度的缺点,以提高残差分析的准确度[6].通过实测数据对各种改进方法进行对比验证,结果显示改进方法均能够明显提高预测的精度.
1 支持向量机
支持向量机SVM能够有效解决复杂的非线性问题,以统计学理论为理论基础.其基本思想是利用内内积函数将非线性变量映射到一个高维特征空间,以结构风险化最小为原则构造最优决策函数,然后在高维空间内线性回归[7].
设一组训练样本:(x1,y1),(x2,y2),…,(xi,yi)∈(Rn×R),对输入样本做如下处理,利用非线性映射φ(x)从原低维空间映射到更高维的特征空间,并构造最优线性拟合函数f(x)=[ω,φ(x)]+b,其中[,]表示内积.以结构风险最小化为原则寻找ω,b,综合考虑模型复杂程度以及泛化能力,寻优过程等价于

式中,ω为权向量,ξ为松弛变量,ξ≥0;C为惩罚参数,C>0,表示在模型复杂和经验风险取一折中,b为一常数,l训练为样本数.
建立Lagrange函数以实现上述优化问题:
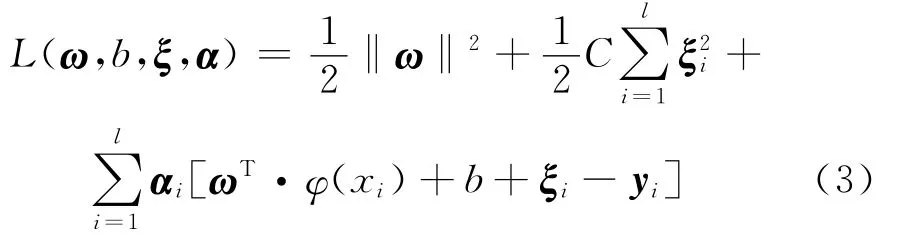
式中,αi为Lagrange乘子.
根据 KKT(Karush-Kuhn-Tucker)条件可得
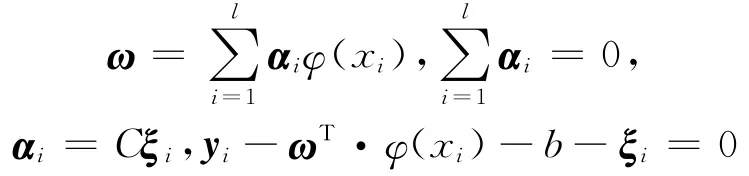
定义核函数k(x,xi)满足 Mercer条件,消去ξi和ω后,得到线性方程组:
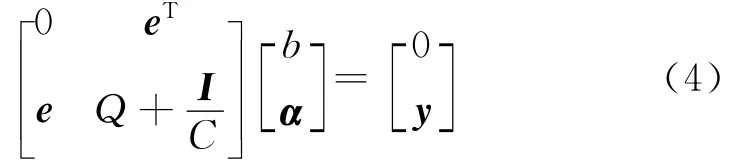
式中:e=[1,1,…,1]T;I为单位矩阵;α=[α1,α2,…,αl]T;Qij=K(xi,xj);i,j=1,2,…,l.
关于核函数,满足Mercer条件即可为核函数,其中径向基核函数(RBF)最为常用:
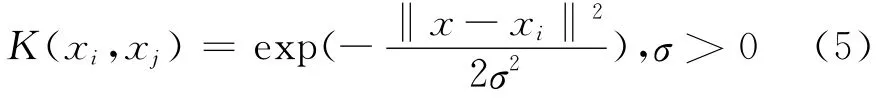
最终可以得到回归模型:
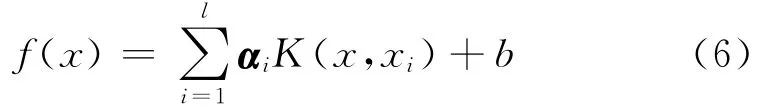
2 马尔科夫链模型
马尔科夫过程[8]是一种具有无后效性的随机过程,马尔科夫链[8]则指的是状态和时间参数均离散的马尔科夫过程.在大坝安全监测数据中,各个测点位移的数值是与时间有关的状态函数,且时间、状态均为离散,可认为是典型的马尔科夫随机过程.
将实测数据按照马尔科夫链的基本原理分成若干状态,分别用E1,E2,E3,…,En表示,按时序依次取t1,t2,t3,…,tn为转移时间,指数列由Ei经k步转为Ej的概率,即

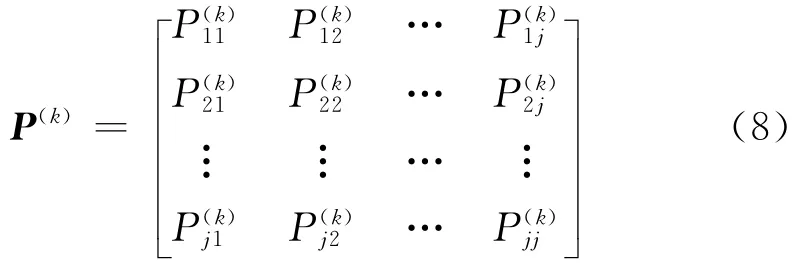
设E1的初始向量V(0),经过k步转移得到的向量V(k)可由下式求得:
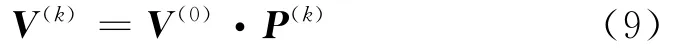
本文根据转移概率在各个状态区间内所占的比重对预测结果进行加权修正,详细过程如下:首先利用APPSO-SVM模型(或SVM模型)求出拟合值和预测值,实测值减去拟合值得残差序列,根据其取值范围划分概率区间,可以通过每个状态向下一时刻的转移概率算出转移概率,进而得到转移概率矩阵[9].预测过程中,选取预测值前面最近的几个(本文取4个)已知所属状态的测值,然后对通过已知状态测值转移到要预测值需要的时步进行统计,并算得相应的Ei(i=1,2,…)步转移概率矩阵,从相应的转移矩阵中找到相应的转移概率,然后统计处于各个状态 的概率,根据计算的概率在不同状态区间内的所占比重按式(11)加权修正:
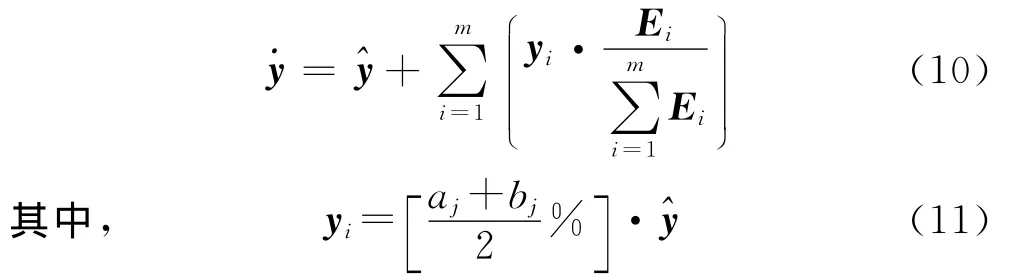
3 改进粒子群优化算法
标准粒子群算法[10]中的粒子通过对自身以及对群体的认识不断对自身的位置进行更新,进而在全局范围内搜索最优解.由于粒子群算法容易陷入局部最优点,对标准粒子群算法进行改进:
1)对惯性因子ω采用线型递减策略[11]:
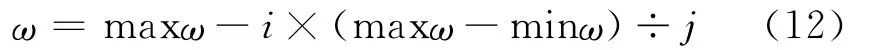
式中,maxω、minω为最大、最小权重值;i为当前迭代次数;j为最大迭代次数.ω的取值范围常取[0.3-0.9].
2)对学习因子c1、c2采用线性学习的方法,c1先大后小,c2先小后大[12]:
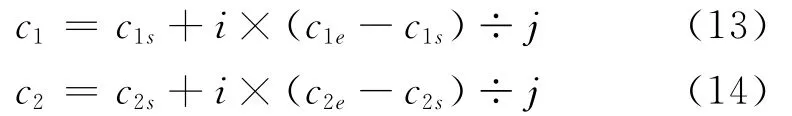
式中,c1s、c2s为c1、c2的迭代初始值;c1e、c2e为c1、c2的迭代终值;i为当前迭代次数;j为最大迭代次数,c1表示变化范围[2.5,1],c2表示变化范围[1.5,2.75].
3)由公式(1)易看出,在进行迭代时,其自身的历史最优值Pi会随着粒子i的位置接近全局最优值Pg而不断接近Pg,从而(1)式后两项近似为0,若粒子的速度也近似为0,由(2)式能够看出粒子的位置不能得到更新,如果此时的“全局最优点”恰为局部最优点,则粒子就会陷入局部最优.因此,引入速度因子υ和位置因子γ(υ,γ≥0),dij=‖Xij-Pgj‖2,表示第i个粒子的第j维的当前位置与全局最优位置的距离.粒子迭代过程中,进行位置和速度更新前进行判断,一旦发现粒子的位置dij<γ,且飞行速度Vij<υ,就可判定粒子出现停滞,立即对粒子的位置进行初始化,防止陷入局部最优.本文利用该改进的PSO算法寻优参数σ和C,达到对SVM模型改进的目的,其中一个粒子代表一个SVM模型.
4 大坝变形预警模型建立
综合前述各理论,大坝变形预警模型流程图如图1,其中适应度的计算在交叉验证(cross validation,CV)意义下的准确率为个体适应度[13].分别按下述流程图求得各改进方法预测值①、②、③、④,然后进行比较分析.
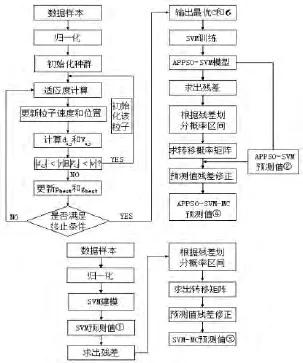
图1 流程图
5 工程应用实例分析
以某水电站实测数据为例,每隔一周选取一组数据,选取2010年7月1日~2012年12月13日实测数据共130组作为训练样本,选取2012年12月20日~2013年2月21日共10组实测值用以预测.
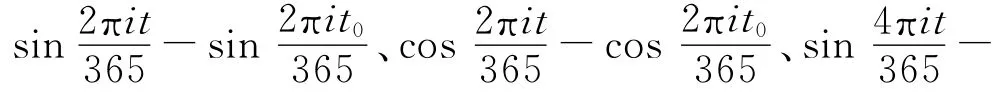
训练样本标准化,设Xmin、Xmax为各组样本数据的最值,标准化后变量:

种群初始化[15]:粒子个数取20个、迭代次数取100,惯性因子ω范围为[0.9,0.3],学习因子c1、c2变化范围分别为[2.5,1]、[1.5,2.75],惩罚因子C与核参数σ范围各为[0.1,100]、[0.01,10].γ=0.1和υ=0.001为核参数σ的位置因子、速度因子,γ=5和υ=0.05为惩罚因子C的位置因子、速度因子.
通过均方差FMSE(式(17))的比较,能更加直观地看出改进方法优越性,SVM模型的拟合均方差为1.907mm,APPSO-SVM 模型的拟合均方差为1.023 mm,SVM-MC模型的拟合均方差为0.968mm,APPSO-SVM-MC模型的拟合均方差为0.578mm.

式中,n为样本数;yi为监测实值为模型计算值.
下面详细介绍APPSO-SVM-MC预测值④计算过程:首先可求得APPSO-SVM模型预测值②以及模型拟合值,将实测值与APPSO-SVM模型拟合值相减可得残差序列,最小值与最大值分别为-1.68 mm、1.86mm,分为4个区间,见表1.利用马尔科夫链进行残差分析,得到转移概率矩阵,见式(18).预测过程中,模型的残差取值若超出所定义区间范围,如果残差大于1.86mm,则归属于状态Ⅳ,如果残差小于-1.67mm,则归属于状态Ⅰ.

表1 概率状态划分
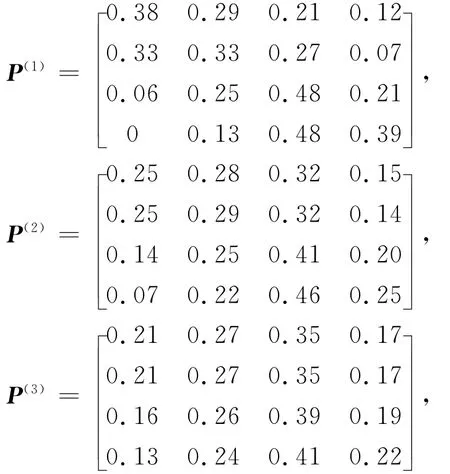

下面预测2012年12月20日位移,以验证其可行性.取预测日期前面4组APPSO-SVM拟合值,进行马尔科夫修正,2012年12月20日所属各状态的概率统计值见表2.
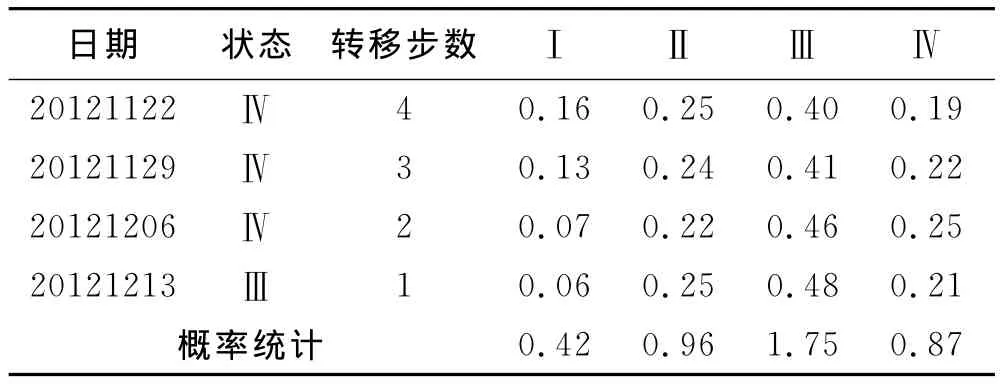
表2 20121220位移所属状态
由APPSO-SVM模型得到20121220的预测值为78.82mm,由公式(11)可计算出经过残差修正后的预测值为79.04mm.

其余日期预测结果依次类推,各改进模型预测结果以及参差值分别见表3和表4.
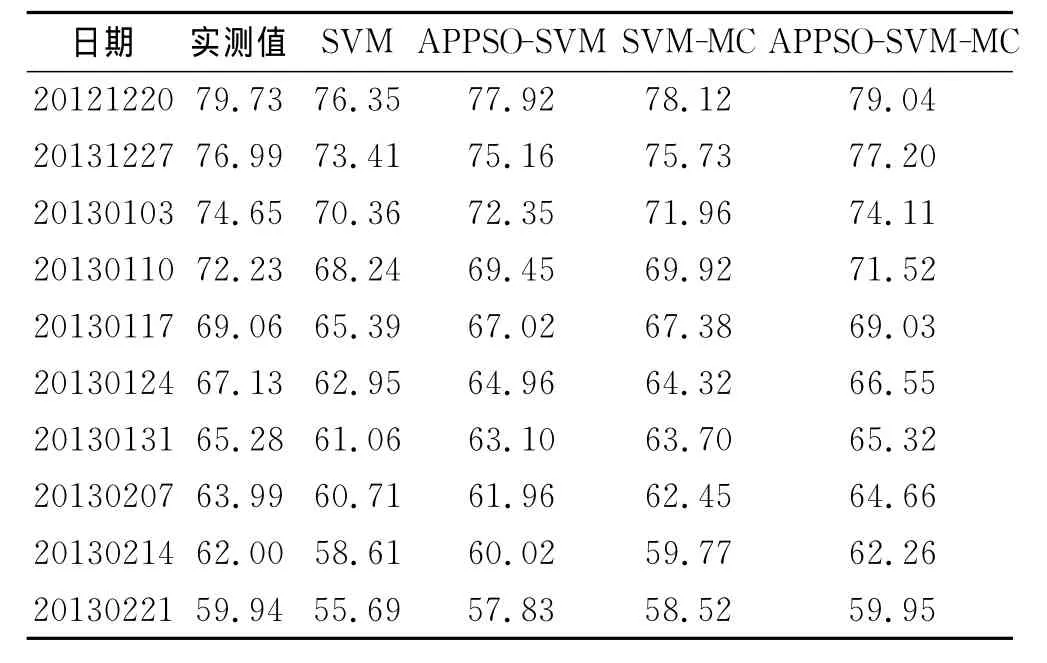
表3 不同改进模型预测值对比
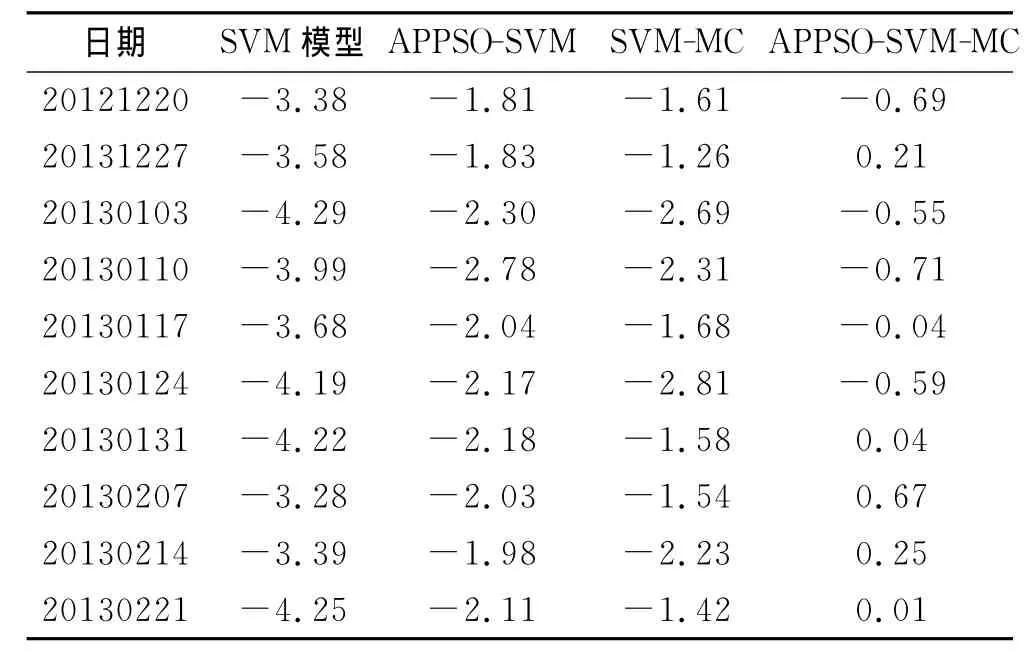
表4 不同改进模型残差对比
SVM-MC模型预测值③的求算方法类似于上述过程,仅需将APPSO-SVM拟合值改为SVM拟合值,其余过程相同.
将不同改进模型的预测值与部分拟合图同基本SVM模型的拟合值与预测值更直观的进行比较,如图2~3所示.由拟合图可以明显看出APPSO-SVMMC模型的拟合精度高于基本的SVM模型;由残差比较与模型预测曲线图可以看出:APPSO-SVM-MC模型的精度最高,APPSO-SVM与SVM-MC模型精度次之,但明显高于基本SVM模型精度,基本SVM模型精度最低.
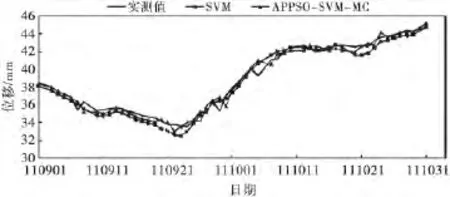
图2 不同模型拟合曲线图

图3 不同模型预测值曲线图
6 结 论
本文以SVM理论为基础,对其改进方法进行比较研究,充分利用粒子群算法快速全局寻优的特点,同时为克服粒子群寻优过程易陷入局部最优点的不足,引入了位置因子和速度因子;利用马尔科夫链模型适用于描述随机波动数据的优点来提高残差辨识的精确性.由实验结果可知本文所提出的改进方法均能有效提高模型的预测精度,将改进PSO算法与马尔科夫链综合对SVM模型进行改进可以大大提高预测精度,而APPSO-SVM模型与SVM-MC模型的预测精度也有较大提高,实际工程中应根据精度需要进行适当选择.综上所述,本文研究的变形预警模型拥有一定的应用价值,可在大坝安全监测领域推广应用.
[1] 田 斌,徐卫超,何薪基,等.前馈人工神经网络法在大坝安全监控中的应用[J].水力发电,2003,29(7):60-63.
[2] 吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.
[3] 于 鹏,顾冲时.大坝安全监测的组合预测模型[J].人民黄河,2006,28(1):67-68,72.
[4] 苏怀智,温志萍,吴中如,等.基于SVM理论的大坝安全预警模型研究[J].应用基础与工程科学学报,2009,17(1):40-48.
[5] 纪雪玲,李 明,李 玮,等.一种克服局部最优的收缩因子PSO算法[J].计算机工程,2011,37(20):213-215.
[6] 张 楠,马福恒,张 帅,等.大坝实测性态的灰色马尔科夫链预测方法研究[J].水电能源科学,2012,30(8):70-73.
[7] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.
[8] 董 胜,刘德辅.年极值水位的灰色马尔科夫预报模型[J].水利学报,1999(1):60-64.
[9] 张 鑫,任永泰,王福林,等.基于改进灰色马尔科夫模型的年降水量预测[J].数学的实践与认识,2011,41(11):51-57.
[10]姜谙男,梁 冰.基于PSO-SVM的大坝渗流监测时间序列非线性预报模型[J].水利学报,2006,37(3):331-335.
[11]刘华蓥,林玉娥,齐名军,等.求解约束优化问题的改进粒子群算法[J].大庆石油学院学报,2005,29(4):73-75.
[12]Asanga R,Saman K H,Harry C W.Self-organizing Hierarchical Particle Swarm Optimizer with Time-varying Acceleration Coefficients[J].IEEE Transactions on Evolutionary Computation,2004,8(3):240-255.
[13]Oh,Hee-Seok Kim,Donghoh Lee,Youngjo et al.Crossvalidated Wavelet Shrinkage[J].Computational Statistics,2009,24(3):497-512.
[14]方卫华.基于峰值识别理论的大坝安全监控模型[J].水电能源科学,2008,26(5):78-79,149.
[15]杨 维,李歧强.粒子群优化算法综述[J].中国工程科学,2004,6(5):87-94.

