含DG配电网潮流算法及在网损分析中的应用研究

王凌云 郑业爽 李 升 邹 燕

（1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.新能源微电网湖北省协同创新中心（三峡大学），湖北 宜昌 443002；3.国网湖北省电力公司，武汉 430077）

0 引 言

分布式电源（DG）并网可以增加电网的稳定性、可靠性和经济性，改善电网的负荷功率因数和电压分布，降低系统损耗等［1－2］.DG并网以后会使得配电网成为一个多电源系统，一些传统的潮流计算方法因不能考虑DG的影响而失效，因此，研究含DG的配电网潮流计算是十分必要的.

DG与传统发电机在配电网中潮流计算中的模型是不同的，DG模型的选取与其运行方式和控制特性有关.王成山等提出DG由恒定阻抗和恒定电压源串联来等效的模型，利用等值阻抗压降和电网电压来求取DG的等值电势［3］.赵晶晶等在前推回代法的基础上，利用正序补偿电流方法处理PV节点，同时采用支路分层技术提高了潮流计算速度，不过计算过程繁琐［4］.文献［5］提出了基于网损灵敏度的分布式发电系统的不平衡三相潮流算法，但在取用灵敏度时采用近似计算，影响了算法的收敛性.牛焕娜等利用配电网各节点电压的相角差不大的特性简化回路电压方程，利用PV节点类型的简化回路电压方程组来计算PV型DG的无功功率值，但算法针对的DG类型单一［6］.文献［7］采用前推回代的配电网潮流算法，研究了分布式电源接入位置和注入容量的改变对配电网网损和电压分布的影响.文献［8］提出了基于牛顿法处理各种DG并网的配电网潮流计算方法，但是牛顿法对电压初值非常敏感，且配电网中的R／X值较大，所以该方法存在收敛困难的问题.

本文分析了几种典型的DG模型，针对前推回代法不能处理PV等类型节点的情况，对潮流计算中节点的无功功率进行修正，将改进的前推回代法应用于含多种DG并网的配电网潮流计算.在IEEE 33节点系统中对算法的可行性和有效性进行了测试和验证.需要说明的是，本文所研究的问题都是在分布式电源并网前，通过一定的控制策略确保其输入有功功率在特定的外界条件下保持恒定的情况.当分布式电源发电的外界影响因素改变时，应用本文所提出的方法，依然能够得出相同的结论.

1 分布式电源并网的节点模型

传统配电网中一般包含平衡节点和PQ节点.变电站出口母线可视为平衡节点，系统中其他节点可看作有功功率和无功功率恒定的PQ节点.各种DG并网以后会使系统潮流计算与传统形式相比变得复杂.随着分布式电源加入配电网，系统中出现了新型的节点：1）P恒定、U恒定的PV节点；2）P恒定、U不定、Q受P和U限定的PQ（V）节点；3）P恒定、电流幅值I恒定的PI节点［9］.

前推回代法计算速度快，编程简单，在分布式电源并网后配电网中出现新型节点和拓扑结构的发生时，能够很方便地进行针对性调整.但在应用该算法的配电网中除平衡节点外，只能有PQ节点存在，需要在已知有功功率P和无功功率Q的前提下进行计算［10］.正是基于此，本文对前推回代潮流计算进行改进，分析各类分布式电源的节点模型，将配电网中出现的PV、PQ（V）和PI型新型节点转化为前推回代法能够处理的PQ型节点，在传统前推回代法中添加无功修正单元，将改进型的前推回代法应用于含DG的配电网潮流计算.

在本文的讨论中，假设整个配电网络是一个吸收型的网络，设定整个系统的负荷总量是大于DG的总容量.

2 改进型前推回代潮流算法的无功修正

2.1 PV节点的无功修正

各类分布式电源中，传统燃气轮机和内燃机等一般采用同步发电机并网，有励磁调节能力.燃料电池通过逆变器并网.此类分布式电源可以处理成PV节点.在第一次迭代取无功功率Q0＝（Qmin＋Qmax）／2.Qmax和Qmin分别为该PV节点的无功功率上下限［11］.部分同步发电机在并网被视为PV节点时，无功功率上下限由同步发电机自身决定，微型燃气轮机等则由作为并网接口的电力电子变换器参数决定.对于PV型的DG，在有功功率不变的情况下，端电压随DG注入无功功率的增大而增大，同时可以提升其他节点的电压.因此，求取PV节点的电压偏差（ΔU）即可对无功功率进行修正，用函数表示为：

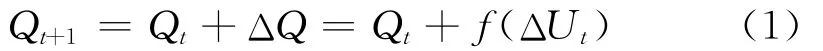
式中，t为迭代次数，ΔQ为无功功率修正值，潮流计算前一次迭代结束后，该PV节点得到电压值U.计算该节点处电压差值：

式中，U0是PV节点的额定电压.

为了探究PV型DG并网时节点处电压差值和无功修正值的关系，不妨假设有N个PV型的DG并入配电网，在所有PV节点处的断开，如图1所示，断点为i1至in.

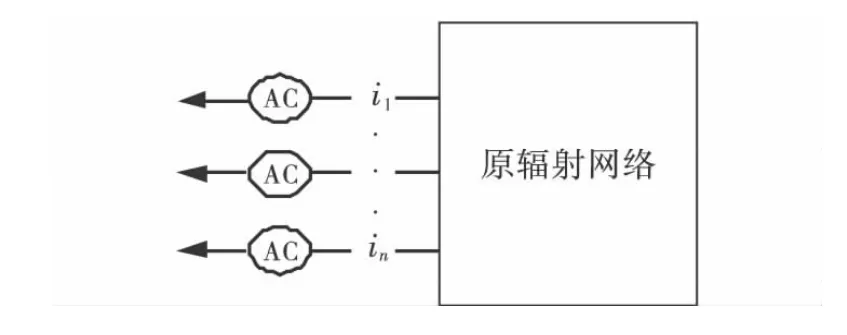
图1 含PV节点的断点网络

新网络仍然是辐射状，取DG的注入电流方向为正方向，从断点处看进去，断点处应满足如下关系：

式中，Δ为各断点处的电压差值组成的矩阵，Δ˙I为各断点处电流变化量组成的矩阵，Z为PV型DG的节点阻抗矩阵.

由复功率计算公式推导得到如下关系：

由于配电网在正常运行的状态下节点电压的标幺值接近于1，且相角θ偏差很小，则得到

将式（5）代入到式（3），得到如下关系：

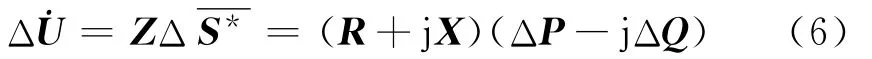
在一般情况下，Δ主要由其实部决定，所以可近似认为：

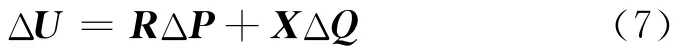
而对于PV型的节点来说，ΔP＝0，变形公式得到PV节点无功功率的差值：

式中，X为PV型DG所在节点阻抗矩阵Z中各元素虚部组成的电抗矩阵.

故PV型DG无功功率修正量ΔQ主要取决于各PV节点的电压偏差ΔU和节点电抗矩阵X，其相关性通过节点电抗矩阵X的逆矩阵来传递.

由以上推导，计算出节点电压差值即可得无功功率差值ΔQ.该差值为修正功率，将其补偿到PV节点原有的无功功率上，得到的新无功功率即可代入到潮流计算的下一次迭代中.

对于PV节点，无功功率存在上下限值，一旦经过修正后的无功功率出现越限，则该PV节点处理为PQ节点，此时节点无功功率等于原本设定的无功功率的上限或下限值.因此，无功修正方程变形如下［12］：

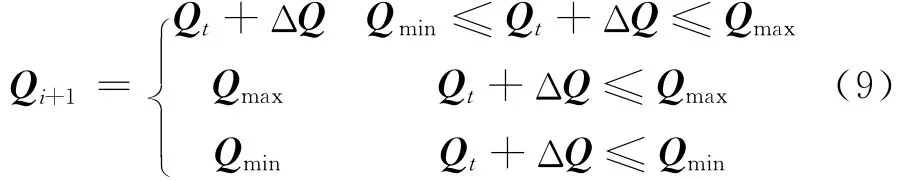
式中，Qmax和Qmin分别为该PV节点的无功功率上下限.

2.2 节点电抗矩阵的形成

在2.1节所提及的电抗矩阵X由如下方法来求解：假设有N个PV型的DG并入配电网，所有PV节点的电抗值可组成电抗矩阵X.这个矩阵X是一个N行N列的方阵.其中，对角元素Xii是第i个PV型DG的自阻抗，其值等于该PV型节点到等效电源节点间所有的支路的电抗之和；非对角元素Xij是第i个和第j个PV型DG之间的互阻抗，它的值等于两个DG到等效电源节点间共同支路的电抗之和.如图2所示.

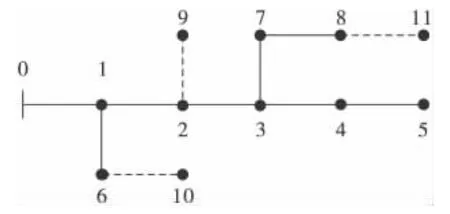
图2 含3个PV节点的网络

在如图2的配电网中，节点9、10、11接入了PV型的DG.则可形成节点电抗矩阵X：

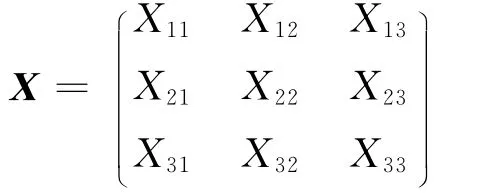
其中，对角元素自阻抗X11、X22、X33分别为：

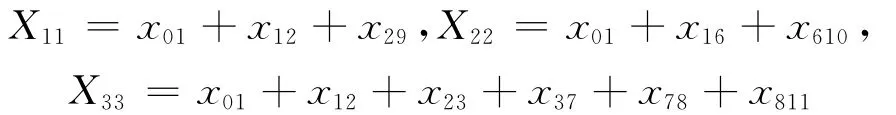
非对角元素互阻抗X12、X21、X13、X31、X23、X32分别为：

式中，x01、x12、x29等值分别为前后两节点号之间对应支路的电抗值.

由线路参数即可确定PV节点对应的节点电抗矩阵X，求逆即可得到能够用于求解修正功率ΔQ的矩阵X－1.

2.3 PI节点的无功修正

以太阳能光伏发电系统和微型燃汽轮机为代表的分布式电源通常经过逆变器接入电网.当逆变器为电流控制型时，在进行潮流计算中此类DG可处理为有功功率和注入电流恒定的PI节点［13］.其注入的无功功率可由前一次迭代的电压值、恒定的有功功率和注入电流值通过下面的公式推算出：

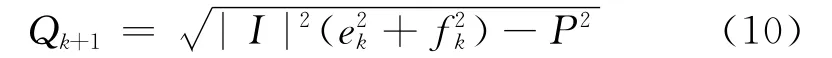
式中，Qk＋1是第k＋1次迭代分布式电源的无功功率值，I是注入电流给定值，ek和fk分别是第k次迭代节点电压的实部和虚部，P是节点有功功率注入.潮流计算时，根据公式（10）对节点的无功进行修正，下次迭代可将PI节点转换成PQ节点计算.

2.4 PQ（V）节点的无功修正

以异步风力发电机和永磁同步发电机为接口并网的DG没有励磁装置，需要电网提供无功功率来建立磁场.

由异步发电机近似等效电路图可知，其无功功率Q与发电机节点电压幅值U、转子电流IR、励磁电流Im、定子电流Is、发电机定子电抗与转子电抗之和xδ，以及励磁电抗xm，转子电阻r，机械负载等效电阻Re，转差率s和电磁功率Pe有关，当有功功率一定时，由近似等效电路可以推导出如下关系：

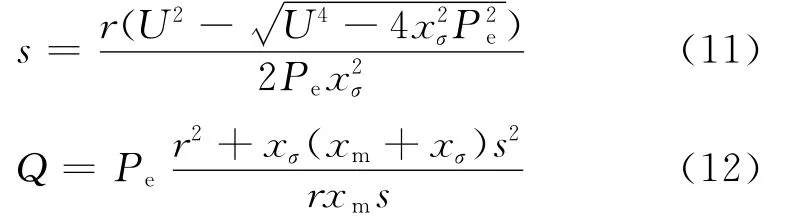
由以上两个式子可以看出，异步发电机在输出有功功率的同时还要从系统吸收一定的无功功率，在有功功率一定的情况下，这类分布式电源的无功功率受节点电压的影响，在潮流计算中可将其看作PQ（V）节点来处理.而对于无功，潮流计算中的迭代方程式可以这样表示：

其中，Ut是第t次迭代得到的电压值.

风力发电系统通过异步发电机并网，利用前推回代法进行潮流计算时，无功功率修正通过公式（11）－（12）实现.

3 改进型前推回代算法的实现

根据前面内容所讨论的几种DG模型的特点，将每种DG对应节点的在潮流计算中的无功修正单元添加到前推回代法的程序中，设计出改进型的算法，本文采用Matlab编制程序，按以下步骤来实现：

1）读取配电网参数，确定并网的DG节点类型和位置.

2）形成节点电抗矩阵，给定最大迭代次数Nmax.

3）初始化网络电压.确定PQ型DG的P、Q值；确定PQ（V）型DG的P、U值，无功功率初值Q0＝f（U），通过公式（11）、（12）进行计算；确定PV型 DG的P、U0值，U0是PV型节点的恒定电压值，无功功率初值取Q0＝（Qmin＋Qmax）／2；确定PI型DG的P、I值，由公式（10）计算其无功功率初值.

4）前推计算：从网络末端节点开始，利用初始电压和功率推算各支路功率损耗和电流值至根节点，得到根节点功率值.

5）回代计算：由根节点功率和电压，计算各节点电压值，直至线路末端.

6）PQ（V）型、PV型和PI型DG无功功率更新：PQ（V）型DG的节点无功功率更新值由公式（11）、（12）计算；PV型DG的节点无功功率补偿由公式（8）计算得出，再将补偿值与原无功功率值相加更新无功功率.PI型DG的节点无功功率更新值由公式（10）计算得出.

7）无功越界判断：计算PV、PI型节点注入的无功功率，若无功功率越界，则将PV或PI节点转变成PQ节点，并修正该节点的注入电流.

8）收敛性判断：所有非PV型节点，求本次迭代的电压幅值Uj（k）与前一次迭代的电压幅值Uj（k－1）之差，PV型节点，求本次迭代的电压幅值Uj（k）与U0之差，若差值均小于ε（ε为收敛指标），则迭代收敛，跳至9）.若不满足，则判断N＞Nmax是否成立（N为迭代次数），若成立则跳至9），若不成立则跳至4）.

9）计算结束，输出潮流计算结果.

4 算例分析

本文采用IEEE 33节点系统，在Matlab环境下测试提出的改进型前推回代法的性能，网络结构如图3所示，节点0为平衡节点，系统母线电压取1.05，基准值SB＝10MV·A，UB＝12.66kV，收敛指标取ε＝10－6.

图3 IEEE 33节点系统

为了验证提出的算法对各种DG并网潮流计算的适用性，本文选取4种类型的DG参与计算.各种DG的配置信息见表1.

表1 不同类型DG的配置信息

4.1 不同类型的DG并网测试

在IEEE 33节点系统中分4种方案接入分布式电源.方案（1）：1个PQ 型 DG并网；方案（2）：1个PI型DG并网；方案（3）：1个PV型DG并网；方案（4）：1个PQ（V）型DG并网；方案（5）：没有DG并网.仿真结果见表2和图4所示.

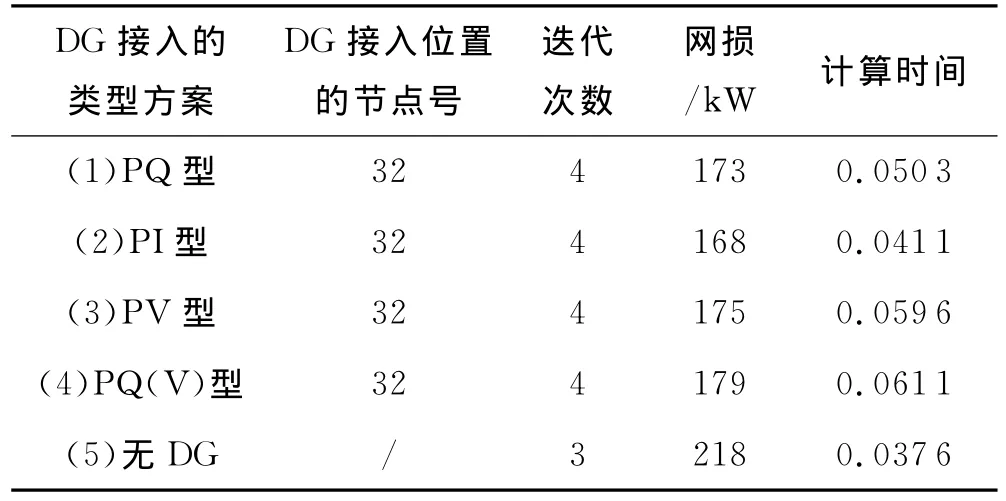
表2 不同类型DG并网测试

各种DG并网后系统各节点电压如图4所示.

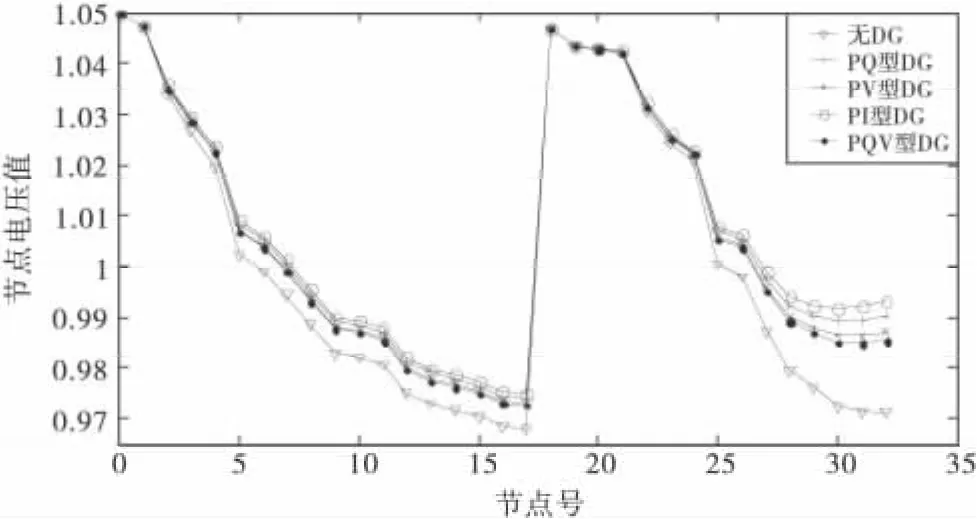
图4 不同类型DG并网节点电压值

从表2可以看出，4种不同类型的DG并网以后，与没接入DG时相比，该配电网潮流计算的迭代次数和计算时间均没有发生很大变化.不同类型的DG并网，迭代次数也没有明显差异.说明本文提出的算法能够用于含分布式电源的配电网潮流计算，且对不同类型的DG都适用.

由图4比较4种DG并网后系统各节点的电压值可以看出，PI型和PQ型的DG相对于PV型和PQ（V）型来说，各节点的电压值较高，对系统电压的支撑作用较强.PQ（V）型DG对电压的支撑能力较其他几种DG来说弱一些，因为其需要电网提供一部分无功功率来建立磁场，因而整个系统的节点电压会相对低一些.含DG的4种方案的系统网损值都小于不含DG的方案对应的网损值218kW，PI、PQ、PV型DG对应的网损分别为168kW、173kW和175kW，PQ（V）型DG对应的网损值为179kW，比其他3种DG并网的网损高，这是因为无功功率在系统中的流动和消耗会增加系统网损.可以看出，转差控制型的异步发电机在作为分布式电源并网的接口时对系统电压的支撑作用不够明显，且网损值较大.在实际应用中，一般选用无功补偿装置进行就地无功补偿，以补偿异步风力发电机从系统中吸收的无功功率.DG并网以后，在有功功率一定的前提下，DG如果能向配电网系统输出无功功率，会使得系统线路中无功功率的流动减少，能提升系统各节点电压值，电压值升高的幅度与无功功率的输出有关.各种类型的DG并网提高了并网节点的电压幅值，同时也带动邻近节点，使其电压幅值也升高.

4.2 不同数量的DG并网测试

在应用的改进型前推回代法进行潮流计算的前提下，讨论不同数量的DG并网对配电网潮流收敛性的影响.设计9种方案，各种方案的迭代次数和计算时间见表3.

表3 不同数量的同种DG并网测试

由表3可知，不同数量DG并网时，对于PQ和PI型的DG，数量的变化没有引起迭代次数的变化，不影响算法的收敛性.而PV型和PQ（V）型的DG，计算的迭代次数与DG数量有着弱关联性，算法的收敛性与没有DG并网时相比有所降低，但变化不是很大.同种DG并网比较，含4个DG的方案系统网损较小，与一个DG并网相比，PI、PQ、PV和PQ（V）型DG网损值分别减小了32.7%、33.5%、35.4%和29.1%，体现了DG并网有降低系统网损的效果.

4.3 同种DG在配电网不同位置并网测试

为了探究DG并网位置的变化对潮流计算的影响，制定9种方案.前4种方案选取17、21、24、32四个节点并入4种类型的DG，与5.2节中一样.第5种方案是没有DG并网的方案.第6至9种方案都选取14、15、16、17四个节点并入DG，这4个节点在一条支路上且位置相邻，每种方案在4个节点并入一种类型的DG.利用本文的改进型前推回代法进行潮流计算，各种DG在不同位置并网迭代次数及计算时间见表4.

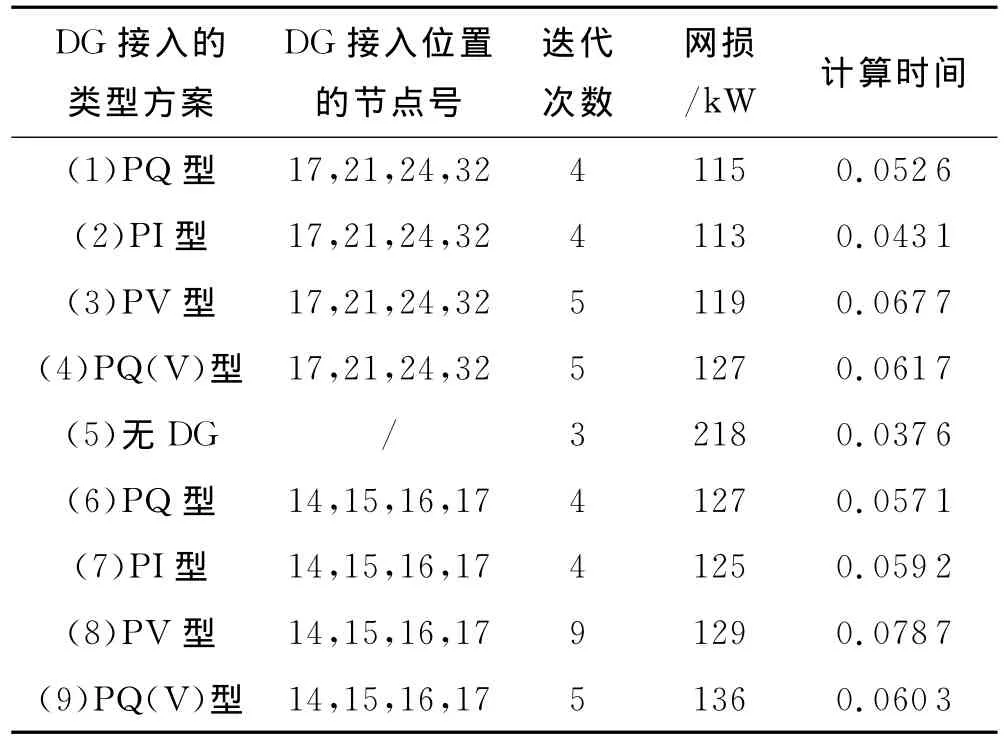
表4 同种DG在配电网不同位置并网测试

由表4可以看出，PQ、PI和PQ（V）型的DG，迭代次数与其并网位置没有关系，且与没有DG并网时的迭代次数差别不明显.而对于PV型的DG，多个DG在同一支路上的并网与在不同支路上并入相同数量的DG相比，潮流计算的迭代次数变化较大.同一支路上多个PV型DG并网，间距较近，在PV型DG之间的线路上有一部分电压降落，由于PV型DG必须保持电压恒定，则需要通过调节无功功率来维持电压不变.在无功功率调节过程中，一旦无功越其上限则PV型节点的无功输入要取无功功率上限值.反之取下限值.此时PV节点转换为PQ节点进行又一次的迭代，这个过程导致迭代次数增加.对于同种DG，在同一支路上4个相邻节点并入4台DG比在4条不同支路末端并入相同数量DG的网损要高.该结论对于不同种类的DG均成立.

4.4 PV型DG以不同的无功初值并网测试

在2.1节中，PV型DG并网时，无功功率初值取Q0＝（Qmin＋Qmax）／2，Qmax和Qmin分别为该PV节点的无功功率上下限，取Q′＝2Q0＝Qmin＋Qmax.结合本文所提出的改进型前推回代法，在PV型DG的有功功率一定的前提下，设计5种方案，无功功率初值按照0.15Q′、0.25Q′、0.5Q′、0.75Q′和Q′选取，探究 PV型DG取不同的无功初值并网对潮流计算有无影响，潮流计算的迭代次数和计算时间见表5.

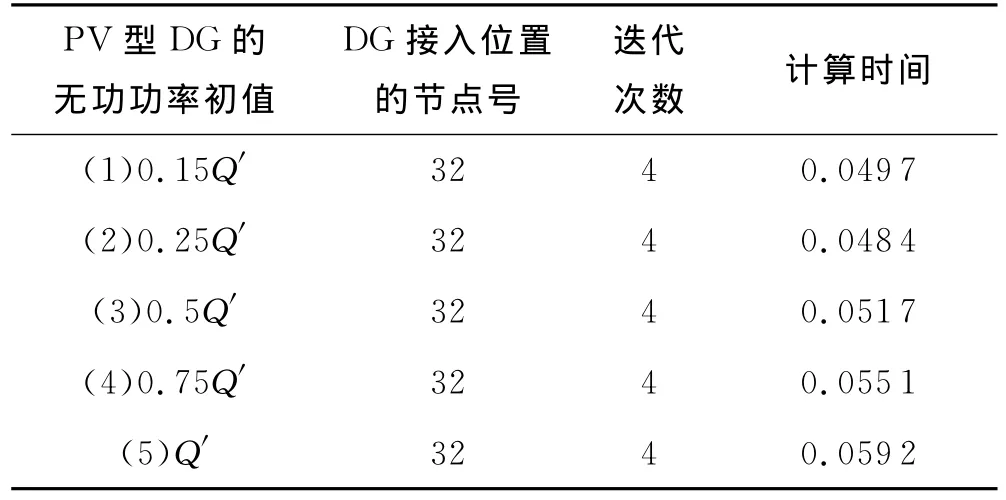
表5 PV型DG以不同的无功初值并网

从表5可以得出，在应用本文所提出改进型的前推回代法前提下，PV型DG并网无功功率初值在一定范围内（0到Qmin＋Qmax）变化并没有影响潮流计算的收敛性，4种方案的潮流计算迭代次数没有变化，均在4次迭代后达到收敛精度的要求，计算时间也非常接近.

5 结 语

在对太阳能光伏发电系统、DFIG以及燃料电池等不同类型的分布式电源进行简要分析的基础上，本文建立了各种分布式电源潮流计算模型.对常用于辐射型配电网潮流计算的前推回代法进行了改进，在此基础上研究了能够适用于各类分布式电源并网的改进型前推回代潮流计算方法，通过算例分析得到了如下结论：

1）本文所研究的改进型前推回代潮流算法能适用于多种DG并网的潮流计算，针对由于分布式电源并网在配电网中出现的PI、PV和PQ（V）等新型节点，考虑到前推回代法不能处理PV等新型节点的问题，探究了潮流计算中各种节点的转化方法，处理方法的本质是在每次迭代中将它们转换成PQ节点.参与并网的DG的种类、数量以及DG并网的形式都不会影响潮流计算的收敛性.计算时间和迭代次数都不会发生很大变化.

2）DG并网对系统电压水平有一定的支撑作用.相同的位置安装不同类型的DG，且DG的有功功率相同，PI型和PQ型的DG对系统的电压支撑能力较强，系统的网损值较低，其中PI型的支撑作用最强.PQ（V）型DG对电压的支撑能力较其他几种DG相对较弱，网损值也较大，因其需要电网提供一部分无功功率来建立磁场，导致整个系统的节点电压会较低.无功功率在系统中的流动和消耗会使得系统网损比其他几种方案高.含DG的4种方案的系统网损值都小于不含DG的方案.

3）对于PQ、PI和PQ（V）型的DG，算法的收敛性与其并网位置没有明显的关系.而对于PV型的DG，与相同数量的DG在不同支路并网相比，同一支路并入多个DG时算法的收敛性较弱.对于4种类型的DG，在同一支路上若干个相邻节点并入若干台DG比在不同支路末端并入相同数量DG的网损要高.

4）运用本文所研究的改进型前推回代法，在处理PV型DG并网潮流计算时，DG的无功功率初值在一定范围内变化不会影响潮流计算的收敛性.

［1］ 王守相，黄丽娟，王成山，等.分布式发电系统的不平衡三相潮流计算［J］.电力自动化设备，2007，27（8）：11－15.

［2］ Augugliaro A，Dusonchet L，Favuzza S，et al.A New Backward／Forward Method for Solving Radial Distribution Networks with PV Nodes［J］.Electric Power Systems Research，2008，78（3）：330－336.

［3］ 王成山，孙晓倩.含分布式电源配电网短路计算的改进方法［J］.电力系统自动化，2013，36（23）：54－58.

［4］ 赵晶晶，李 新，许 中.含分布式电源的三相不平衡配电网潮流计算［J］.电网技术，2009，33（3）：94－98.

［5］ 李红伟，张安安.含PV型分布式电源的弱环配电网三相潮流计算［J］.中国电机工程学报，2012，32（4）：128－135.

［6］ 牛焕娜，井天军，李汉成，等.基于回路分析的含分布式电源配电网简化潮流计算［J］.电网技术，2013，37（4）：1033－1038.

［7］ 刘 磊，江 辉，彭建春.分布式发电对配电网网损和电压分布的影响［J］.计算机仿真，2010（4）：279－283.

［8］ Thomson M，Infield D G.Network Power－Flow Analysis for a High Penetration of Distributed Generation［J］.IEEE Transactions on Power Systems，2007，22（3）：1157－1162.

［9］ 陈海焱，陈金富，段献忠.含分布式电源的配电网潮流计算［J］.电力系统自动化，2006，30（1）：35－40.

［10］王艳玲，韩学山，周晓峰.含分布式电源的主从联合系统扩展连续潮流计算［J］.电工技术学报，2012，27（9）：93－100.

［11］杨旭英，段建东，杨文宇，等.含分布式发电的配电网潮流计算［J］.电网技术，2009，33（18）：139－143.

［12］韩 洲，任永峰.基于分布式电源的微电网建模与仿真［J］.计算机仿真，2014，31（5）：120－124.

［13］杨 超，沈 聪，李 睿.含分布式电源配电网的前推回代潮流算法中PV节点处理方法［J］.电网技术，2012，36（9）：238－243.