基于AHP－熵权法的黄河下游堤防安全模糊评价

何晓洁 赵二峰

（1.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学 水资源高效利用与工程安全国家工程研究中心，南京 210098）

黄河是我国的第二大河流，从20世纪60年代以来，随着水沙条件和边界条件的变化，泥沙主要淤积在相对宽阔的两岸大堤之间，形成突出于两岸滩地的河床，即二级悬河—悬河中的悬河［1］.自郑州桃花峪以下786km的黄河河段为黄河下游，是典型的游荡性河段，现行堤防大部分是在旧堤基础上加修而成的，与国内外其它江河堤防相比，黄河下游堤防工程有其显著的特点：黄河下游堤防地质条件复杂、隐患多；黄河下游河道堤基条件差，堤身土质强度不够、结构疏松、渗透性大；黄河河势变化没有得到有效控制，黄河洪水特征变化较大，其堤防安全的动态性较明显.近年来，在堤防安全评价方面，尤其以日本、荷兰为代表，根据自身土质条件、外力条件、受灾历史等因素构建了符合各自国家实际情况的安全评价体系.目前，我国的堤防研究主要局限在堤防渗流、岸坡稳定性等［2］，尚未形成系统的安全评价理论.因此，本文首先提出AHP－熵组合确定权重的方法，然后应用模糊数学理论，通过构建黄河下游堤防综合评价层次结构，利用AHP－熵权法确定各指标的权重，从而通过最大隶属度对黄河下游堤防安全进行模糊评价.

1 AHP－熵权法

目前，权重确定的方法很多，大致可以分为两类：主观赋权法和客观赋权法.主观赋权法是依据各指标的主观重视程度进行赋权，如专家咨询法、层次分析法（Analytic Hierarchy Process，简称 AHP）［3］、乘积标度法等；客观赋权法是指依据决策矩阵提供的信息来确定，如主成分分析法、因子分析法、投影追踪法、熵值法、BP神经网络等.下面主要研究AHP法与熵值法相结合的方法来确定指标权重.

1.1 AHP法确定主观权重

AHP法是先从层次结构模型的第2层开始，对于从属于（或影响）上一层每个因素的同一层诸因素，用成对比较法和1－9比较尺度构造判断矩阵，直到最下层，然后由判断矩阵计算指标权重向量并做一致性检验.常用的标度方法有9／9－9／1标度、10／10－18／2标度、指数标度等，形成的判断矩阵为正互反矩阵.指标权重的计算方法通常有算术平均法、几何平均法、特征根方法等，其中判断矩阵的一致性问题是一个难点，可凭借经验性估计来调整判断矩阵.

以A表示目标，ui表示评价因素，ui∈U（i＝1，2，…，n），uij表示ui对uj（j＝1，2，…，n）的相对重要性数值，uij取值见表1.

表1 判断矩阵标度

由各标度值的意义得到判断矩阵U如下

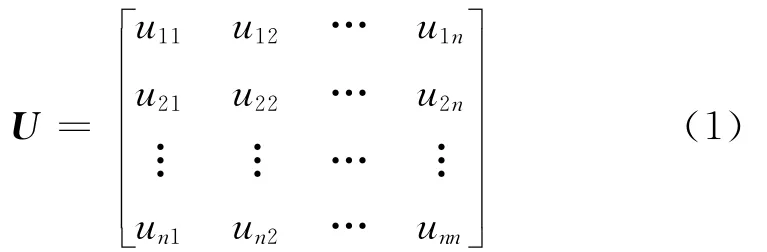
由矩阵U求出最大特征值所对应的单位特征向量，所求单位特征向量各分量即为各评价因素重要性排序.因此，权重分配的计算可归结为计算满足Uω＝λmaxω的特征根和特征向量，将特征向量正规化，并将正规化得到的特征向量ω＝［ω1，ω2，…，ωn］作为本层次元素的排序权值，ωi和λmax的计算如下

为了检验权重的分配是否合理，需要对判断矩阵进行一致性检验

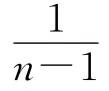
表2 判断矩阵的平均随机一致性指标

当CR＜0.1时，即认为判断矩阵具有满意的一致性，说明权重系数分配合理.否则就需要调整判断矩阵，直到取得满意的一致性为止.

1.2 熵值法确定客观权重

在信息论中，熵是系统无序程度的量化，可以用来评估已知数据包含的有效信息量和确定权重［4］.熵值法由评价指标构成的判断矩阵来确定指标权重，当评判对象在某项指标上的值相差较大时，熵值较小，说明该指标提供的有效信息量较大，该指标的权重也应较大.熵值法能尽量消除各因素权重的主观性，使评价结果更符合实际.

设有n个指标的m次评价结果，其初始矩阵X＝［xij］m×n，采用极差变化法，得到标准化后矩阵Y＝［yij］m×n，则第j项指标的信息熵：

式中：

k与系统的样本数有关，当系统的有序度为0时，其熵值最大.m个样本无序分布时，fij＝1／m，则

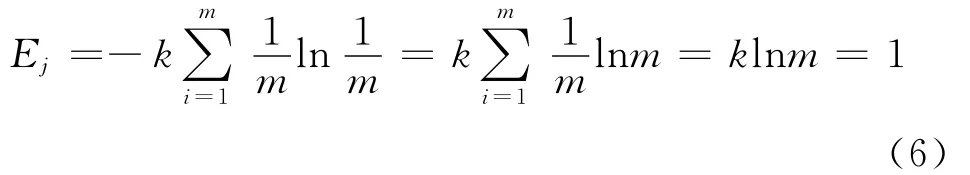
当lnfij＝0时，fijlnfij＝0；当lnfij＝1时，fijlnfij＝e.当信息熵完全无序时，对诊断的效用也为0，因此某项指标的效用值取决于信息熵Ej与1的差值Hj：

某指标的信息效用值越大，则其对评价结果的重要性就越大，即其所占的权重也越大，所以信息效用值与权重的概念是一致的.将信息效用值标准化，即可得到各个指标的权重：

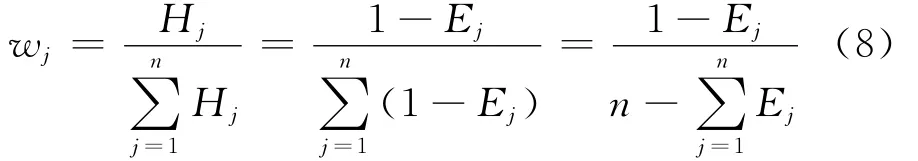
1.3 AHP－熵组合确定最终权重

下面建立基于最小二乘的主客观权重组合法.设有m个评价对象，n个评价指标，标准化后的决策矩阵为Y＝（yij）m×n，则第i个评价对象的评价值为

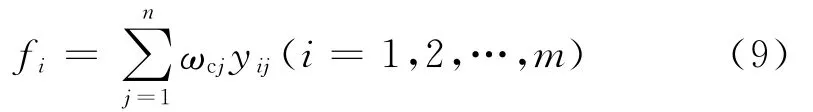
设AHP法对n个评价指标所赋权重为Wz＝［ωz1，ωz2，…，ωzm］T，熵值法对n个评价指标所赋权重为Wk＝［ωk1，ωk2，…，ωkn］T.对所有评价对象的所有评价指标而言，AHP－熵组合赋权所得的指标权重的偏差应越小越好.为此建立如下最小二乘优化模型，即

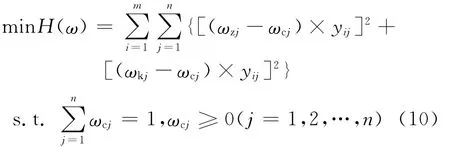
式中，ωcj为第j个评价指标的最小二乘组合后的主客观组合权重.求解式（10）即可得到第j个指标的最小二乘组合后的主客观组合权重ωcj.

2 黄河下游堤防安全模糊评价

下面利用模糊数学理论，通过建立黄河下游堤防安全的评价集和隶属函数，构建模糊矩阵，确定各评价指标所属隶属度，通过模糊矩阵和权重的模糊运算进行黄河下游堤防安全综合评价.

2.1 黄河下游堤防综合评价层次结构

黄河作为“地上悬河”，其危险性与危害性远大于一般河流，其安全性除与自身结构特点有关外，河势和渗透边界对其安全也有重大的影响，如堤身的土质特性、断面形式及大小、堤身隐患、防护措施和除险加固措施等以及洪水特性及河势变化等［5］，这些不同的影响因素需通过具体的指标来体现.根据黄河下游堤防工程特点，建立如图1所示的三级（目标层、准则层、因素层）评价指标体系，其中洪水荷载是黄河下游堤防最重要的荷载，且河道本身的游荡性、河道断面特性以及堤防受保护情况对工程安全造成影响.另外，黄河下游堤防的安全性受其堤身和堤基特性的影响，同时堤防护坡和截渗墙等加固措施也起到作用.

图1 黄河下游堤防安全综合评价指标体系

2.2 确定评价集

参照我国大坝安全状况的划分（水利部.水库大坝安全鉴定办法［S］.2003－271），有｛正常，基本正常，不正常｝的3级划分，也有｛正常，基本安全，轻度不安全，不安全，很不安全｝的5级划分.针对前述黄河下游堤防工程的动态安全状况，传统的3级、5级划分法比较不适用于堤防工程，笔者认为需对较安全的情况进行一定程度的区分，由此确定黄河下游堤防4级划分的评价集：｛安全，较安全，一般安全，不安全｝.

2.3 确定隶属函数

隶属函数的确定具有一定的主观性，本文通过专家打分法将定性指标转化为定量指标，然后再确定其隶属函数，隶属函数构造如下：

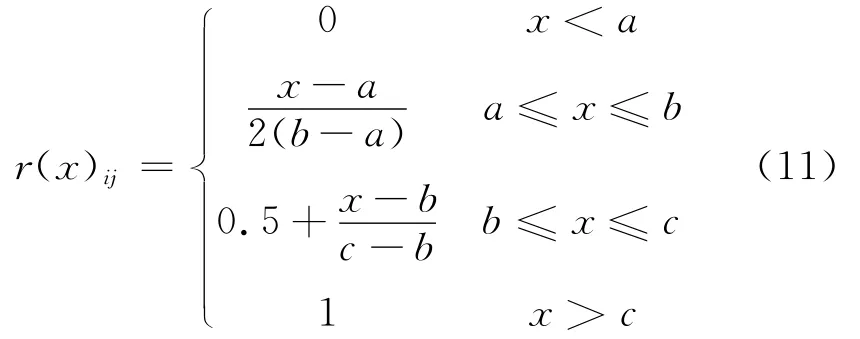
式中，x为各个因素的实际专家打分值，a、b、c分别为堤防评价分级的标准值.

本文构建如表3所示的评价集和其所对应的分级标准值，a、b、c对应的取值应分别为60、70和90.

表3 评价集和其对应的分级标准值

由式（11）即可确定对应于各评价指标的模糊隶属度矩阵R.

2.4 综合评价

利用最终确定的组合权重P和模糊隶属度矩阵R相乘，并进行归一化处理，可得对应于各个评价集的隶属度.根据最大隶属度原则，确定黄河下游堤防安全状态，据此对黄河下游堤防安全性进行综合评价.

3 工程实例

本文采用文献［6］的济南市天桥区段堤防实例，该堤段属一级堤防，该段堤防建国后经过4次加高培厚而成，堤身填土以壤土、砂壤土为主，夹杂少量粉砂，土质复杂，施工质量较差；堤基土质以粘土、砂壤土为主，中间夹杂粉细砂互层.历史险情主要为堤身渗水，且堤基没有采用防渗加固措施.根据评价指标体系（图1），3位堤防专家对该堤段安全特性进行打分，其结果见表4.

表4 堤防安全特性指标打分结果

1）根据AHP法求得因素层对标准层的主观权重集为：ωz1＝（0.624 5，0.168 8，0.168 8，0.038 0），ωz2＝（0.268 4，0.049 5，0.114 7，0.567 5），ωz3＝（0.333 3，0.333 4，0.333 3），ωz4＝（0.283 7，0.391 4，0.041 2，0.110 1，0.173 6），ωz5＝（0.571 4，0.285 7，0.142 9），ωz6＝（0.455 0，0.141 1，0.141 1，0.262 7）.

2）根据熵权法求得因素层对标准层的客观权重集为：ωk1＝（0.463 2，0.171 0，0.171 0，0.194 8），ωk2＝（0.779 0，0.169 5，0.193 2，0.459 3），ωk3＝（0.330 6，0.338 9，0.330 6），ωk4＝（0.283 7，0.391 4，0.041 2，0.110 1，0.173 6），ωk5＝（0.571 4，0.285 7，0.142 9），ωk6＝（0.457 4，0.173 1，0.192 4，0.177 2）.

3）采用最小二乘法确定的最终主客观权重集为：ωc1＝ （0.543 9，0.170 0，0.170 0，0.116 1），ωc2＝（0.223 2，0.109 5，0.154 0，0.513 3），ωc3＝（0.332 0，0.336 0，0.332 0），ωc4＝（0.283 7，0.391 4，0.041 2，0.110 1，0.173 6），ωc5＝（0.565 1，0.246 0，0.188 9），ωc6＝（0.456 2，0.157 1，0.166 8，0.211 9）.

4）标准层对目标层的主客观权重集为：QA＝（0.231 1，0.101 0，0.057 8，0.247 3，0.247 3，0.115 6）.

5）由隶属函数确定的模糊隶属度矩阵如下：

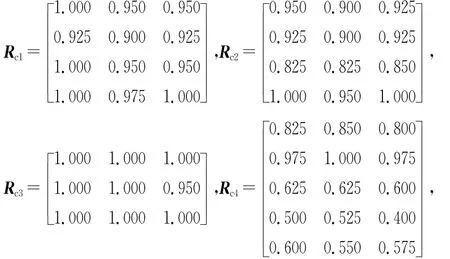
6）对济南市天桥区堤防各层所属安全等级进行综合判定，分别为：

由此可得，济南市天桥区堤防的安全等级对应的隶属函数值为0.812 9，对应的安全等级为较安全.但由于该堤段堤基没有采用防渗加固措施，当遭遇汛期洪水时，该堤段将发生流土或滑坡失事破坏，需通过除险加固提高该堤段的服役可靠性.

4 结 语

本文针对黄河下游堤防安全评价，首先，采用主客观组合赋权的方法，将层次分析法和熵权法有机结合用以确定各评价指标权；然后根据黄河下游堤防工程特点及其影响因素，建立了3级（目标层、准则层、因素层）评价指标体系，并确定了黄河下游堤防4级划分的评价集，通过构造隶属函数，根据最大隶属度原则，确定了黄河下游堤防安全状态.工程实例分析表明，评价模型中AHP－熵权法综合考虑了专家的主观意愿与客观事实，使得权重的确定更具科学性和合理性，能够为我国堤防安全评价及除险加固提供可靠的依据.

［1］ 杨吉山，许炯心，廖建华，等.不同水沙条件下黄河下游二级悬河的发展过程［J］.地理学报，2006，61（1）：66－76.

［2］ 毛昶熙，等.堤防工程手册［M］.北京：中国水利水电出版社，2009.

［3］ 孙宏才，等.网络层次分析法与决策科学［M］.北京：国防工业出版社，2011.

［4］ （美）格 雷.熵与信息论［M］.北京：科学出版社，2012.

［5］ 张瑞怡，戴其祥，董美丽，等.黄河下游堤防隐患特征与治理对策［J］.人民黄河，2001，23（9）：10－11.

［6］ 张秀勇.黄河下游堤防破坏机理与安全评价方法的研究［D］.南京：河海大学，2005.