多孔介质冰蓄冷板的融化过程

刘小平，蒋玉龙，张素军，李菊香

（1南京工业大学产业处，江苏 南京 211816；2南京工业大学能源学院，江苏 南京 211816）

相变储能是利用相变介质进行相变潜热的释放或储存的技术[1]，因具有潜热量大、相变过程等温等优点，越来越受到人们的重视。相变材料在电力“移峰填谷”、太阳能热利用、建筑节能等工业或民用领域广泛应用[2-4]。开孔泡沫金属因具备优良的热力、力学性能，已被应用于填料、紧凑型热交换器等的制造[5-6]。将高导热性能的开孔泡沫金属填充入相变介质，可提高复合相变材料的综合导热性能，改良相变储能过程[7-9]。Siahpush 等[10]研究表明，在纯度为99%正二十烷的中填充孔隙率95%的泡沫铜，能将复合材料热导率从0.423W/(m·K)提升到3.06W/(m·K)。吴志根等[11]实验研究结果表明：泡沫金属和膨胀石墨能有效提高高温相变蓄热系统的换热能力。高导热性能多孔介质的孔隙参数会对相变过程产生影响。王杰利等[12]研究认为，孔隙率对相变热阻具有较大影响，适当减小孔隙率可有利于增强热传导。杨秀等[13]模拟研究发现，泡沫铝的孔隙率越小，融冰所需时间越少，蓄冰球的有效容积也越小。Shiina 等[14]研究认为，多孔泡沫金属的最佳孔隙率随蓄热系统传热系数的增加而有所降低。

对于相变介质中填充高导热性能的多孔介质以缩短相变时间的研究，很多学者已做了大量的工作。然而实际过程中，部分相变介质自身的热导率已经满足要求，需要的是通过延长相变时间来控制相变过程的释冷速率。如采用复合材料制成冰蓄冷板满足某些制冷设备的需求。对于将低导热性能的多孔介质填充入固液相变介质构成复合相变材料、延长相变时间的研究鲜见报道。为此，本文提出了在纯冰中填充导热性能相对较低的网状聚氨酯多孔介质，对其融化过程进行了数值模拟和试验研究，旨在研究网状聚氨酯多孔介质相关参数对延长冰蓄冷板工作时间的影响规律。作为对比，本文还研究了填充高导热性能泡沫金属的冰蓄冷板融化过程。

1 数值模拟

冰蓄冷板的物理模型如图1 所示，模型的左、右两侧面处在对流环境中，其余的上、下、前、后各面均为绝热，冰蓄冷板中填充开孔泡沫，左、右两侧的环境温度分别为TL和TR，表面传热系数分别为hL和hR。

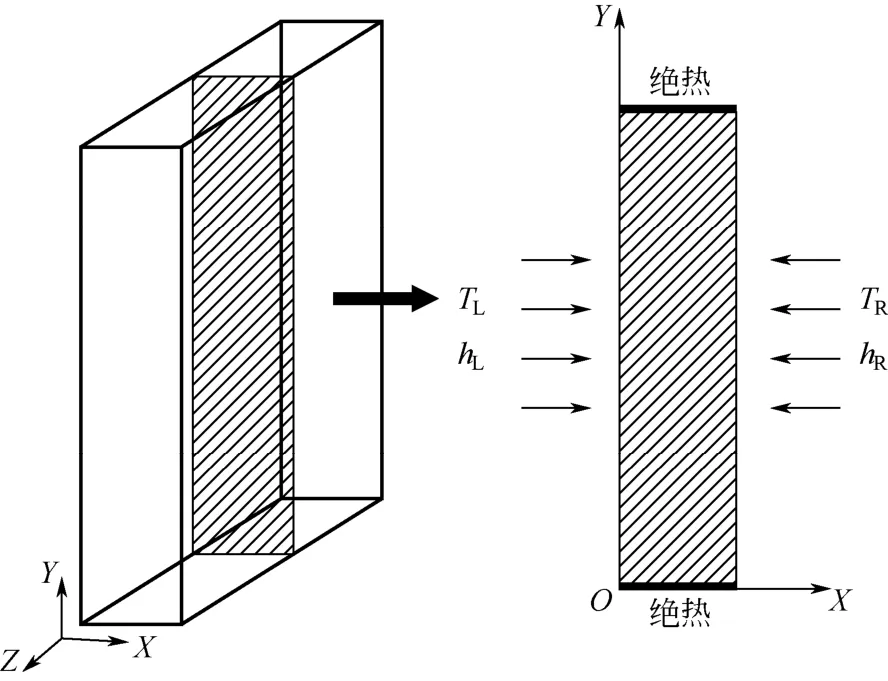
图1 冰蓄冷板的物理模型

采用Fluent 中的焓-多孔理论模拟融化和凝固问题。该理论将温度和焓均作为待求函数，建立统一的能量方程，以液相率表示两相区中的液相体积分数，且假设液相率与温度呈线性变化关系，通过 不断更新计算区域内每个单元的液相率来追踪固液两相界面的变化[15]。简化假设如下：①环境空气为层流，且与固体壁面处于局部热平衡；②复合相变材料为各向同性，初始温度均匀；③相变介质的流体为不可压缩牛顿流体，层流，流体与固体间处于局部热平衡，忽略黏性耗散，密度服从Boussinesq假设；④相变介质在固、液两态时为常物性，但在熔融状态时热物性参数只随温度线性变化。

质量、动量和能量守恒方程[16]分别如式（1）～式（3）。

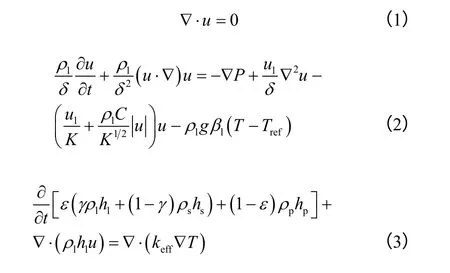
多孔介质的渗透系数K、惯性系数C 和有效热导率keff采用如式（4）～式（6）的表达式[17]。

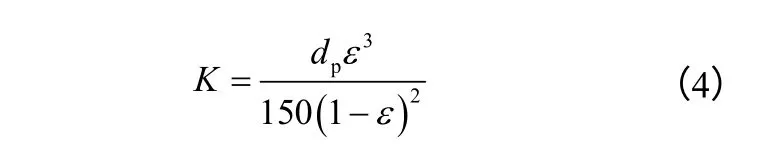
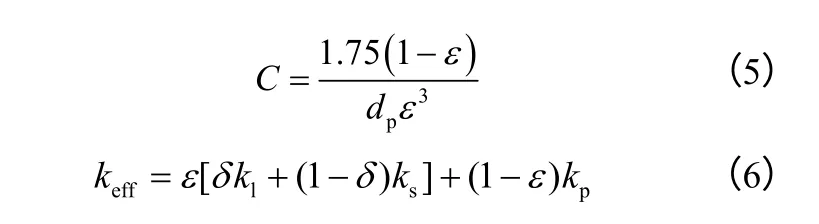
式中，dp为多孔介质的平均孔直径。

由于在粥状区，融化具有一定的温度范围，液体所占的体积单元分数δ(t)由温度来确定[18]，如 式（7）。

初始条件如式（8）。

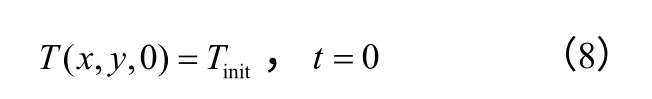
边界条件如式（9）、式（10）。

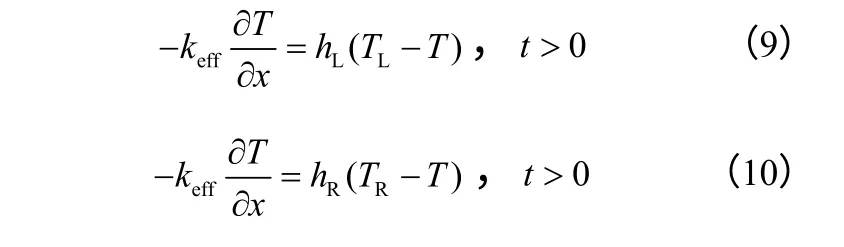
式中，Tinit为初始温度，K。

使用Gambit 软件建立模型并采用结构化划分网格，网格选用四边形，网格尺寸精度为1mm，冰蓄冷板的计算网格如图2 所示，其中GZ指向Z 轴的正方向（垂直于纸面向外）。

采用SIMPLE 处理速度和压力场耦合，固壁边界。初始温度设为268K。冰的凝固和液化温度分别设为271.2K 和273K。融化过程中，从固相区到液相区，冰在孔隙中所占的体积分数由100%线性变化到0。在每个时间步长内对各控制方程进行耦合迭代计算，直至结果收敛。相关的材料热物性参数如表1[19]所示。

图2 网格划分

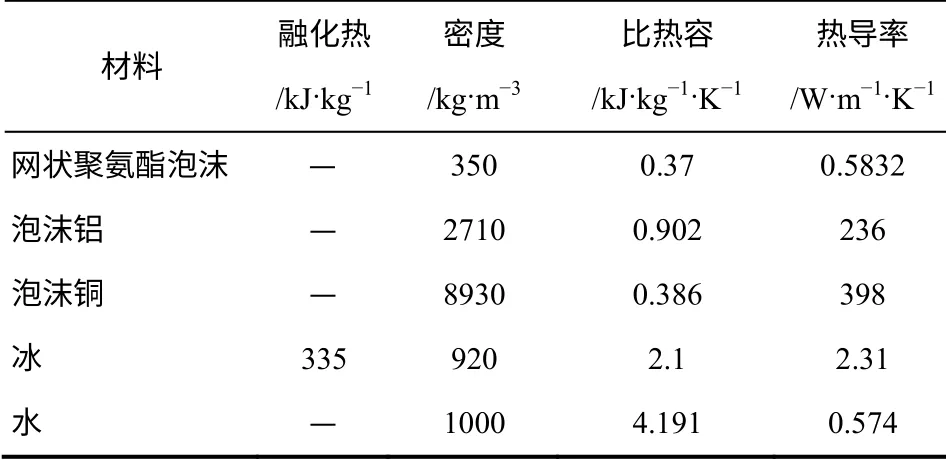
表1 材料热物性参数

2 模拟结果及分析

2.1 多孔介质的热导率对温度分布的影响

图3 为融化时间约4h 时的冰蓄冷板温度分布，ω为孔密度，ppi 指每英寸长度的毛孔目数。

由图3 可见，各冰蓄冷板中相变介质均未完全融化，处于固液共存状态。横向上，板内外壁最大温差，泡沫金属冰蓄冷板(b)和(c)小于纯冰蓄冷板

(a)；纵向上，温度分布，泡沫金属冰蓄冷板(b)和(c)比纯冰蓄冷板(a)的更均匀，这些说明与纯冰蓄冷板相比，泡沫金属冰蓄冷板的温度分布更佳。这可能是由于金属的高导热性能所致。金属的导热远远大于纯冰，添加泡沫铜或泡沫铝后，冰蓄冷板整体热扩散能力得到很大提升，冰蓄冷板外壁的热量能够迅速地传向内部，不仅不会出现“热堆积”现象，而且由于金属骨架的作用，热量能够更好地分散到蓄冷板的各部分。并且，泡沫铜冰蓄冷板(c)的温度分布略优于泡沫铝冰蓄冷板(b)，这是由于铜的热导率高于铝所致。

图3(d)是网状聚氨酯泡沫冰蓄冷板的温度分布，比较网状聚氨酯泡沫冰蓄冷板(d)和纯冰蓄冷板(a)发现，不论纵向上和还是横向上，两者温差接近，前者稍高于后者。出现这一结果，可能是聚氨酯泡沫的热导率小于纯冰（近似为纯冰的1/4），网状聚氨酯泡沫冰蓄冷板的整体冰蓄冷板的导热能力小于纯冰蓄冷板，热扩散能力减小，使得传热速率减小；此外，在一定程度上，网状聚氨酯泡沫的多孔特性抑制了融化介质的自然对流，阻碍了冰水分层，降低了不同温度区域的交互作用。

2.2 多孔介质的热导率对相界面的影响

图4 为融化时间约4h 时冰蓄冷板的相界面情况。

由图4 可见，融化相同时间后，纯冰蓄冷板(a)内部出现了明显的固液相界面轮廓，下端出现半椭圆弧状相界面，圆弧上方为尚未融化的固态介质，下方红色区域为已融化的液态介质，两区域间为固

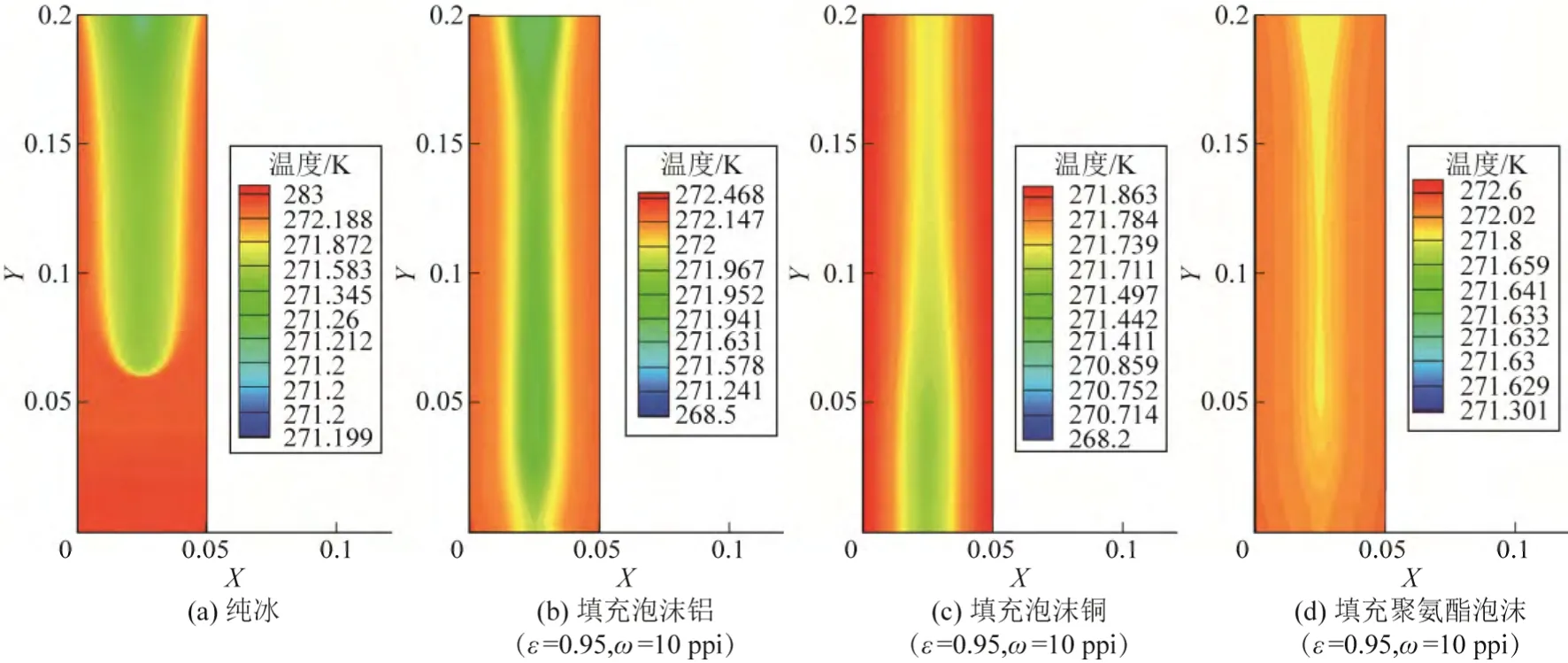
图3 冰蓄冷板温度分布

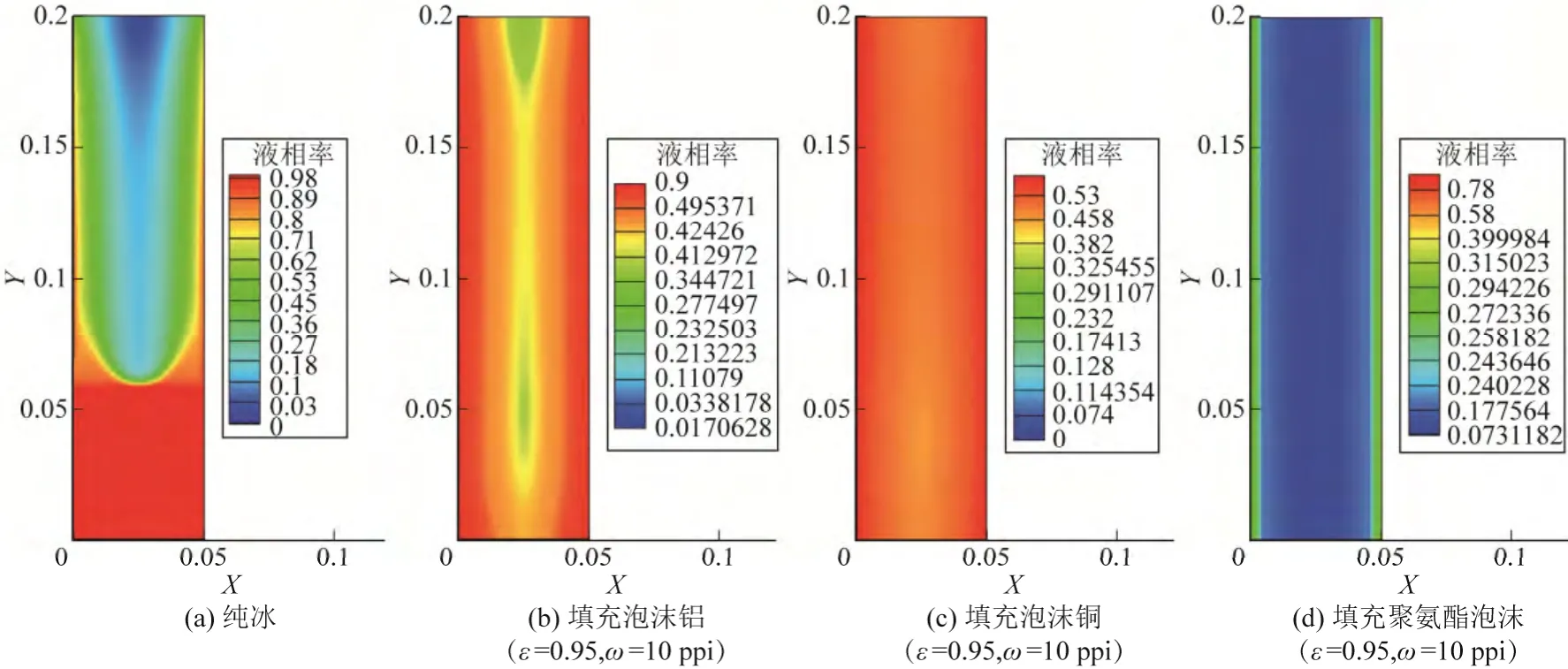
图4 冰蓄冷板相界面

液共存的糊状区；相比较之下，泡沫金属冰蓄冷板(b)和(c)内部的固液相界面形状较模糊。出现这一情况的原因可能是：①泡沫金属冰蓄冷板的整体导热性能高于纯冰蓄冷板，热扩散性好，温度分布均匀，融化过程在更大的区域进行，不会出现纯冰时“上液下固” 明显的相界面分层；②泡沫金属的多孔性可能抑制了冰水混合物中的自然对流，从而下段未出现由于固液密度差引起的半椭圆弧状相界面；③还可能是泡沫金属冰蓄冷板的融化速率快，已融化相变介质的液相率较高，弱化了固液区域分层。对比网状聚氨酯泡沫冰蓄冷板(d)和纯冰蓄冷板(a)可见，网状聚氨酯泡沫冰蓄冷板内的液态区面积小于纯冰的，这表明网聚氨酯泡沫的低导热性能减小了冰的融化速率，延长了冰蓄冷板的工作时间。此外，聚氨酯泡沫冰蓄冷板内固液相界面分布要比纯冰的更加模糊，这可能同样是由于聚氨酯泡沫的多孔特性抑制了固液的自然对流所致，导致渗透性减小，渗透系数下降，降低了融化速率。

2.3 多孔介质的热导率对融化时间的影响

图5 是填充相同孔隙参数的不同多孔介质时冰蓄冷板内的液相率随时间的变化。

由图5 可见，添加多孔介质后，冰蓄冷板的融化时间随填充材料导热能力的增加而减小。这是由于添加高导热能力的泡沫铜或泡沫铝时，可以有效提高复合相变材料的热导率，从而加快融化速率，缩短融化时间。铜的热导率高于铝，所以添加泡沫铜后，融化时间更短。相反，添加低导热能力的网状聚氨酯降低了复合相变材料的热导率，使融化速率减小，融化时间延长。

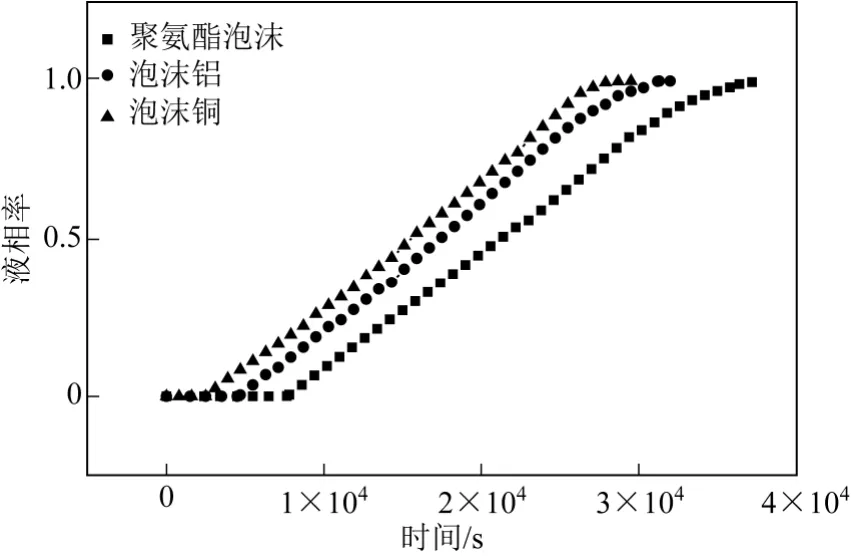
图5 热导率对液相率的影响

2.4 多孔介质的孔隙率对融化时间的影响

图6 是多孔介质的不同孔隙率（孔密度为10ppi）条件下冰蓄冷板内的液相率随时间的变化。

由图6(a)和(b)可见，填充泡沫金属时，冰蓄冷板的冰融化时间随孔隙率的增加而延长，泡沫铜冰蓄冷板的融化时间受孔密度变化的影响大于泡沫铝冰蓄冷板的；由图6(c)可见，当填充网状聚氨酯泡沫时，融化时间随孔隙率的减小而缩短。原因可能如下：①热导率的影响，填充泡沫金属使得冰蓄冷板导热能力增大，且孔隙率越小，导热能力越大，融化时间越短；填充网状聚氨酯泡沫使得冰蓄冷板导热能力减小，且孔隙率越小，导热能力越小，使得融化时间越长；②相变介质的质量比例影响，随着孔隙率的减小，冰的质量分数会有所减少，这可能也导致相变介质融化时间缩短。

2.5 多孔介质的孔密度对融化时间的影响

图7 分别为填充泡沫铝、泡沫铜、网状聚氨酯泡沫的不同孔密度（孔隙率为0.95）时，融化过程中液相率随时间变化的影响。由图7(a)和图7(b)可见，孔隙率一定时，泡沫金属的孔密度对融化过程的影响较小。表明对于高热导率材料，高孔密度对自然对流的削弱作用大于增加表面积对换热的强化作用。由图7(c)可见，孔隙率一定时，网状聚氨酯泡沫的孔密度对融化过程的影响较大。随着孔密度增大，融化时间延长，表明对于低热导率材料，高孔密度对自然对流的较大的削弱作用抑制了热量的传递。对比图6 和图7 发现，泡沫金属孔隙率对融化速率的影响作用大于孔密度。

3 试验结果及讨论

分别对填充泡沫铜和网状聚氨酯泡沫复合相变材料的冰蓄冷板进行了融化时间的测定。试验用到 的多孔介质表征参数见表2。

图6 孔隙率对液相率的影响

冰蓄冷板的尺寸均为：长×宽×高=20cm×10cm×5cm。试验条件设定如下：TL=TR=293K，hL=hR=8W/(m2·K)。冰蓄冷板初始温度均为268K。根据测量冰层厚度随时间的变化，可计算出液相率随时间的变化；同时将融化产生的液态水收集，也可以测算出液相率。试验过程的液相率结果取这两种不同方法的算术平均值。试验台示意如图8。

3.1 多孔介质的热导率对冰蓄冷板融化过程的 影响

图9 是填充孔隙率均为0.95、孔密度均为10ppi的泡沫铜和网状聚氨酯泡沫的冰蓄冷板释冷过程中的液相率随时间变化的测定结果。

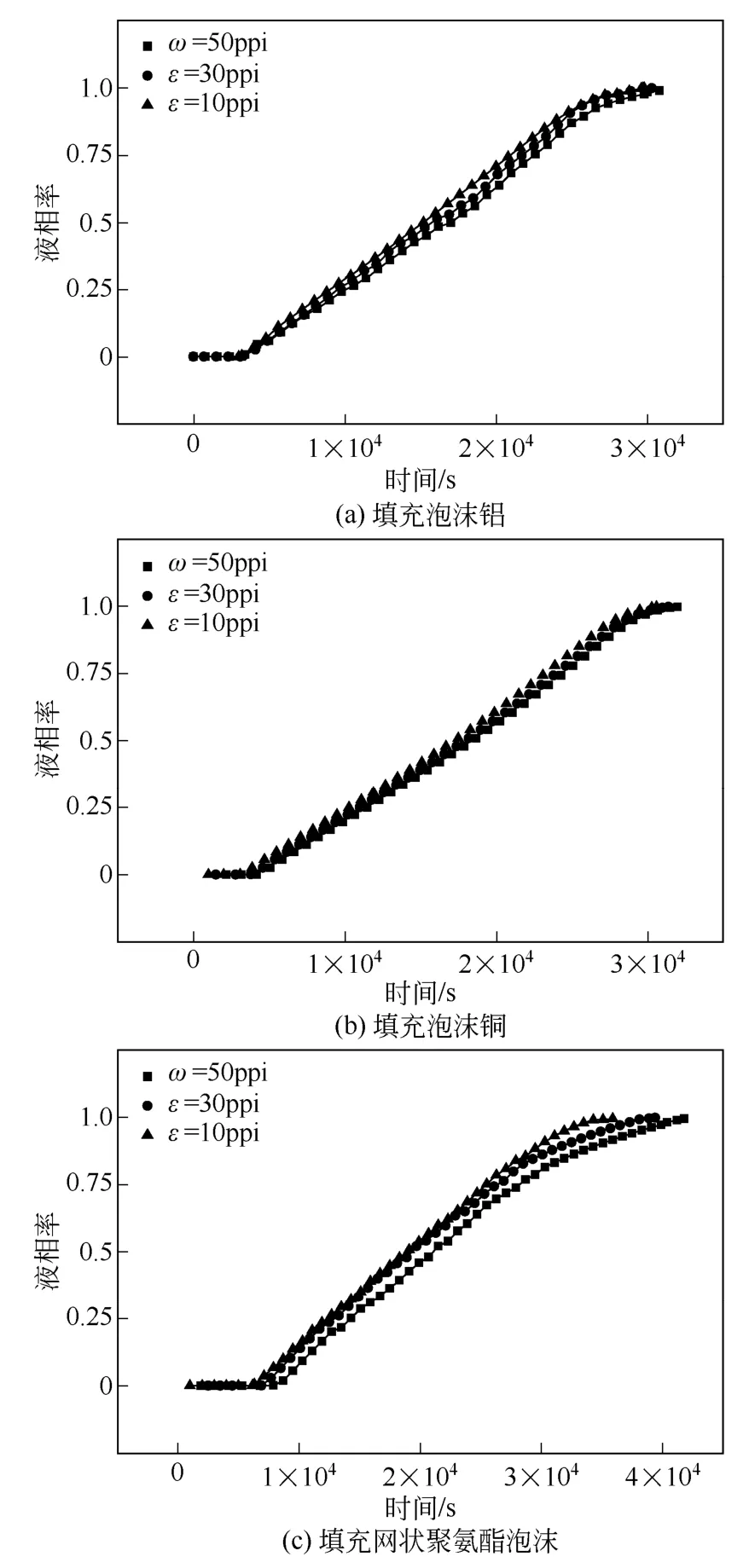
图7 孔密度对液相率的影响

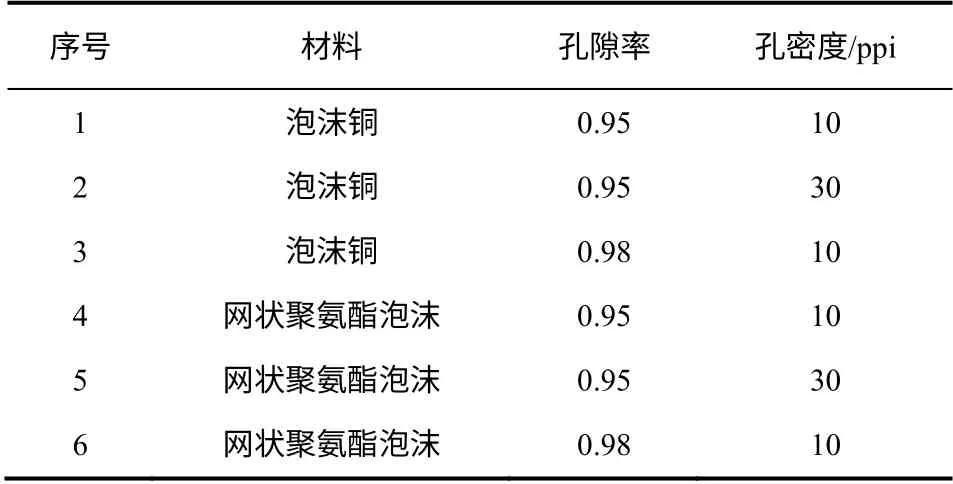
表2 试验用多孔介质表征参数

由图9 可见，初始时刻各冰蓄冷板的液相率均为0，这表明由于初始时刻各冰蓄冷板的温度远低

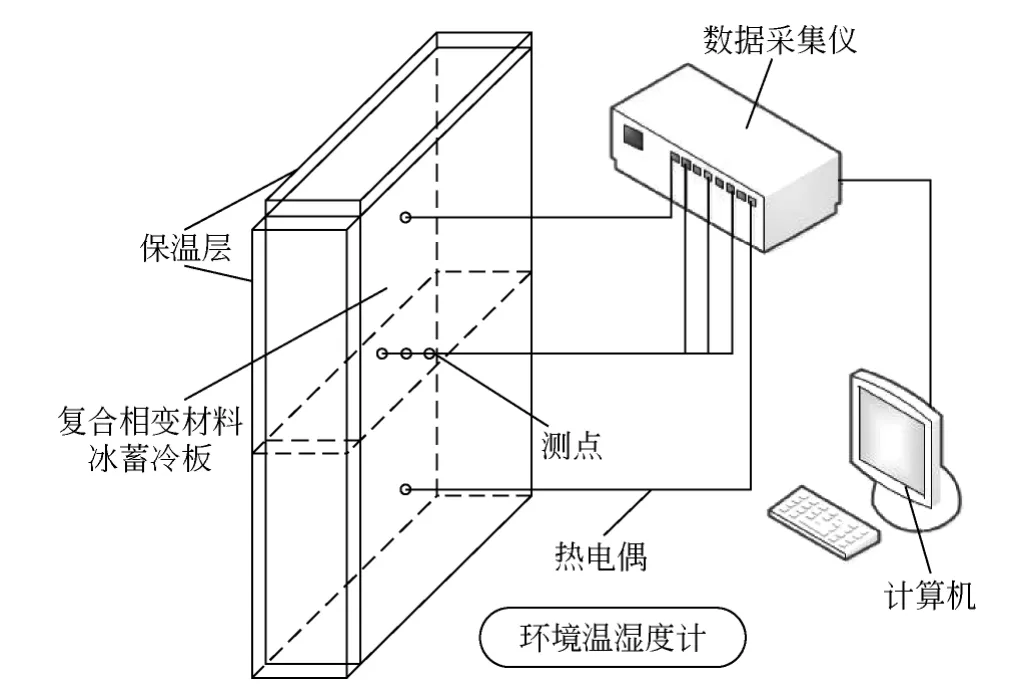
图8 试验台示意图

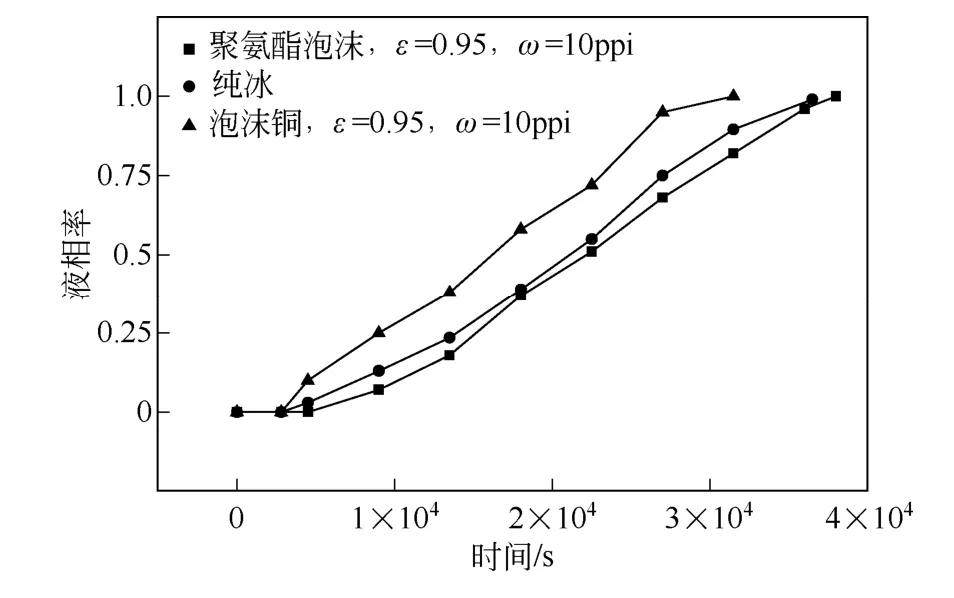
图9 不同热导率多孔介质下液相率随时间变化的 曲线

于其相变温度，此时与环境间属于显热交换，尚未发生相变，因而无液体水产生。当经历一时间段后，填充泡沫铜的冰蓄冷板液相率首先开始出现变化，这表明其先于填充网状聚氨酯泡沫的冰蓄冷板到达相变温度。此后，两者的液相率均随时间延迟而提高，并且在相同时刻，填充泡沫铜冰蓄冷板的液相率均高于填充聚氨酯泡沫。最终，填充泡沫铜冰蓄冷板的液相率先达到100%，这表明其已经完全融化。填充泡沫铜冰蓄冷板的融化时间比填充网状聚氨酯泡沫缩短21%。这是由于铜的热导率远大于网状聚氨酯泡沫，使得泡沫铜冰蓄冷板的总体换热效果要优于聚氨酯泡沫冰蓄冷板的，故前者融化速率要高于后者。

3.2 多孔介质的孔密度对冰蓄冷板融化过程的 影响

图10 是纯冰与填充孔隙率均为0.95、不同孔密度的泡沫铜和网状聚氨酯泡沫冰蓄冷板释冷过程中的液相率随时间变化的测定结果。

由图10(a)可见，10ppi 的网状聚氨酯泡沫冰蓄冷板的融化速率快于30ppi 的。与纯冰相比，10ppi的网状聚氨酯泡沫冰蓄冷板可将释冷时间延长9.8%，ω=30ppi 的可延长14.3%。表明孔密度对融化过程产生了影响，说明低孔密度对冰融化过程中冰水间的自然对流具有较小的抑制作用，验证了模拟分析结果。对比图7 和图10，曲线的整体趋势较为一致，具有较高的吻合度，也证明了模型的可 靠性。

图10 不同孔密度下液相率随时间变化的曲线

由图10(b)可见，10ppi 的泡沫铜冰蓄冷板的融化速率快于30ppi 的。与纯冰相比，10ppi 的泡沫铜冰蓄冷板可将相变时间缩短15.2%，30ppi 的缩短11.4%。这表明高热导率的多孔介质其孔密度对融化过程的影响较大。孔密度较低时，平均孔径相对较大，孔隙对自然对流的抑制作用较小，对于融化过程中的热交换有利，可提高融化速率。

3.3 多孔介质的孔隙率对冰蓄冷板融化过程的影响

图11 为纯冰与填充孔密度均为10ppi、不同孔隙率的泡沫铜和网状聚氨酯泡沫冰蓄冷板释冷过程中的液相率随时间变化的测定结果。

由图11(a)中可见，ε=0.95 的网状聚氨酯泡沫冰蓄冷板的液相率和ε=0.98 的差别很小，两者的融化速率基本一致。与纯冰相比，前者可将释冷时间延长9.8%，后者延长11.8%。这表明，对于低热导率 的多孔介质，孔隙率对融化速率影响较小，远小于孔密度的影响，这和模拟结果较为一致。

图11 不同孔隙率下液相率随时间变化的曲线

由图11(b)中可见，ε=0.95 的泡沫铜冰蓄冷板的融化速率明显快于ε=0.98 的。与纯冰相比，前者可以将融化时间缩短15.2%，后者可缩短8.1%。这是由于孔隙率相对较低时，多孔介质在复合相变材料中所占体积较大，高热导率的多孔介质会使得冰蓄冷板的整体导热性能提高，因而加快了融化速率。这也表明，对于高热导率多孔介质，孔隙率对融化速率影响较大，大于孔密度的影响，这和理论模拟结果的趋势也较为一致，具有较高的吻合度。

4 结 论

本文通过对填充多孔介质冰蓄冷板融化过程进行模拟和试验研究，对比了不同表征参数的多孔介质对冰蓄冷板融化过程的影响。结果显示：多孔介质的热导率会对冰蓄冷板融化速率产生较大影响。与纯冰相比，本研究中热导率较高的泡沫铝、泡沫铜等可以将冰蓄冷板融化时间缩短最多达15.2%，冰蓄冷板的融化速率会随孔隙率或孔密度的减小而增加，孔隙率变化对融化速率的影响更大。热导率较低的网状聚氨酯泡沫可以将冰蓄冷板释冷时间延长最多达11.8%，冰蓄冷板的释冷时间随孔隙率或孔密度的增大而增加，孔密度变化对释冷时间的影响更大。

符 号 说 明

C—— 惯性系数，m-1

Cp—— 比热容，J·kg-1·K-1

dp—— 多孔介质的平均直径，m

h—— 对流换热系数，W·m-2·K-1

K—— 渗透系数，m2

k—— 热导率，W·m-1·K-1

L—— 融解热，J·kg-1

T—— 温度，K

V—— 体积，m3

ε—— 孔隙率

γ—— 液体所占孔隙分数

δ—— 液体所占体积单元分数

ρ—— 密度，kg·m-3

ω—— 孔密度，ppi（单位英寸孔目数）

下角标

eff—— 有效的

init—— 初始时刻

L—— 冰蓄冷板左侧

l—— 液态相变介质

liquid—— 融化

p—— 多孔介质

pcm—— 相变介质

R—— 冰蓄冷板右侧

s—— 固态相变介质

solid—— 凝固

[1] Zalba B，Marín J M，Cabeza L F，et al. Review on thermal energy storage with phase change：Materials heat transfer analysis and applications[J]. Applied Thermal Engineering，2003，23：251-283.

[2] 马素德，宋国林，樊鹏飞，等. 相变储能材料的应用及研究进展[J]. 高分子材料科学与工程，2010，26（8）：161-164.

[3] 于欣，胡晓峰，黄占华. 有机/复合相变储能材料研究进展[J]. 功能材料，2012，43（B08）：16-21.

[4] Rozanna D，Chuanh T G，Salmiah A，et al. Fatty acids as phase change materials（PCMs） for thermal energy storage：A review[J]. International Journal of Green Energy，2005，1（4）：495-513.

[5] 汪双凤，李炅，张伟宝. 开孔泡沫金属用于紧凑型热交换器的研究进展[J]. 化工进展，2008，27（5）：675-678.

[6] 张龙龙，龚峻松，宋光涛，等. 泡沫金属填料旋转床用于CO2的吸收[J]. 化工进展，2012，31（10）：2157-2161.

[7] Jegadheeswaran S，Pohekar S D. Performance enhancement in latent heat thermal storage system：A review[J]. Renewable and Sustainable Energy Reviews，2009，13（9）：2225-2244.

[8] Mesalhy O，Lafdi K，Elgafy A，et al. Numerical study for enhancing the thermal conductivity of phase change material（PCM） storage using high thermal conductivity porous matrix[J]. Energy Conversion and Management，2005，46（6）：847-867.

[9] Martin V，He B，Setterwall F. Direct contact PCM-water cold storage[J]. Applied Energy，2010，87（8）：2652-2659.

[10] Siahpush A，O’Brien J，C’repeau J. Phase change heat transfer enhancement using copper porous Loam[J]. Journal Heat Transfer，2008，130：1-11.

[11] 吴志根，赵长颖，顾清之. 多孔介质在高温相变蓄热中的强化换热[J]. 化工学报，2012，63（s1）：119-122.

[12] 王杰利，屈治国，李文强，等. 封装有相变材料的金属泡沫复合散热器实验研究[J]. 工程热物理学报，2011，32（2）：295-298.

[13] 杨秀，陈振乾. 蓄冰球中填充泡沫铝的融化相变传热过程的数值模拟[J]. 化工学报，2008，59（s2）：139-142.

[14] Shiina Y，Inagaki T. Study on the efficiency of effective thermal conductivities on melting characteristics of latent heat storage capsules[J]. International Journal of Heat and Mass transfer，2005，48（2）：373-383.

[15] ANSYS Inc. ASNSY FLUENT12.0 Theory Guide[M]. USA：ANSYS Inc.，2009

[16] 卢涛，姜培学. 多孔介质融化相变自然对流数值模拟[J]. 工程热物理学报，2005，26（6）：167-170.

[17] 林瑞泰. 多孔介质传热传质引论[M]. 北京：科学出版社，1995：111-128.

[18] 郭宽良，孔祥谦，陈善年. 计算传热学[M]. 合肥：中国科学技术大学出版社，1988：68-69.

[19] 阚安康，韩厚德，汤伟. 基于分形理论的开孔聚氨酯泡沫等效热导率研究[J]. 材料导报，2012，26（2）：143-146.