木材热物理参数理论表达式的推导及其计算值与实测值比较

林 铭 ,杨庆贤 ,饶久平 ,谢拥群 ,廖益强 ,魏 微

(福建农林大学材料工程学院 ,福建福州350002)

木材热物理参数理论表达式的推导及其计算值与实测值比较

林 铭 ,杨庆贤 ,饶久平 ,谢拥群 ,廖益强 ,魏 微

(福建农林大学材料工程学院 ,福建福州350002)

利用木材热物理参数3个理论表达式分别计算28种木材的比热容、导热系数和导温系数 ,并分别与同条件下的实测值相比较.结果表明:28种木材理论计算的平均误差分别为2.6%、5.7%、6.7%；最大误差分别为8.0%、12.8%、12.5%.木材热物理常数3个理论表达式都不是通常依据试验数据拟合成的经验方程式 ,而是依据统计力学和物理学原理 ,经过数学推导得到的理论表达式 ,使之学术上具有内在的理论意义.

木材；热物理参数；理论表达式；统计热力学；类比推理法

木材是三大建筑工程材料之一.木材的比热容、横纹导热系数和导温系数是木材热工程应用和木材改性、防腐等热加工处理以及木材科学研究中的重要热物理参数.由于木材解剖结构的复杂性、化学组成的多样性、物理性质的各向异性等复杂因素 ,导致从机理上研究木材热物理参数有极大困难.因此 ,国内外学者一般都是从试验上直接研究木材的热物理参数 ,从中获得试验数据后 ,或以列表形式、或通过数学拟合成各种经验方程式[1－13]等表示木材的热物理参数.

本文将应用统计热力学和类比法[14－18],推导木材的比热容、横纹导热系数和导温系数3种热物理参数的理论表达式.应用这3个理论表达式分别计算28种木材的比热容、导热系数和导温系数 ,同时分别应用Dunlap[12]和Кириллов[13]比热经验方程式以及Maclean[4]和Gu-Audrey[11]横纹导热系数公式作对比计算 ,最后均以试验数据进行验证.

1 木材比热容理论表达式的推导

木材的各种物理性质主要取决于组成木材细胞壁的物质结构[19].已知纤维素是构成木材细胞壁的主要物质.纤维素大分子的基本化学结构单元是D-吡喃葡萄糖(C6H10O5) ,以β-1 ,4—糖苷键联接而成的没有分支的链状分子 ,其化学结构式如图1所示.

图1 木材纤维素的化学结构式Fig.1 Chemical structure of wood cellulose

应用X射线衍射 ,结果表明:一切天然纤维素具有相同的晶体结构.纤维素晶体含有结晶区和无定形区[20],结晶区的分子链排列最有规则 ,呈现出清晰的X射线衍射图.无定形区的分子链排列的规则性较差 ,但也并非完全无序 ,仍有相当的规则性 ,取向大致与纤维轴平行.结晶区与无定形区之间没有明显界限 ,而是逐渐过渡的.

按照经典统计热力学[21],一个含有N个分子 ,每个分子由S个原子组成的分子晶体 ,可以有3S组不同的简正振型和频率.其中每一组振型都有较高和较低两个频率与之对应.频率较高的称为光学振型 ,频率较低的称为声学振型.由N个声学振型组成的每一组贡献出一个德拜项 ,而由N个光学振型组成的每一组贡献一个爱因斯坦项.于是 ,由一摩尔分子组成的晶体 ,其摩尔热容为

对于由吡喃环构成的木材纤维素来说 ,要确定吡喃环质心的位置 ,需要3个平动自由度 ,又因吡喃环呈环状结构 ,不能看作质点 ,还需3个转动自由度.这6个自由度满足声学色散关系 ,它们各自贡献一个德拜项.这也意味着(1)式中的a＝2.

20个原子(S＝20) ,共有60个自由度.除了平动和转动6个自由度外 ,还有54个自由度 ,它们均属于吡喃环内各原子的振动自由度 ,包括C—C ,C—H ,C—O ,O—H各键的伸缩与挠曲运动.它们均属于光学振型.各贡献一个爱因斯坦项.此外 ,C—O键强度与环内键强度相近.但环上的键成环状结构 ,看作一个整体 ,贡献德拜项 ,而两环之间的这个氧原子因其质量远小于作为整体的吡喃环总质量 ,因而不能构成德拜项.因此 ,这3个自由度亦属光学振型 ,各贡献一个爱因斯坦项.由此可从(1)式得到绝干木材的比热表达式

式中μ是葡萄糖基的摩尔质量.

为简化(2)式的计算 ,可利用热力学温度T与摄氏温度t之间的关系 ,把(2)式C0(T)在T0处展开为泰勒级数 ,取到t的一次项 ,并代入已知数据 ,整理后再利用绝干木材比热容C0(T) ,推出含水率为W%的湿木材的比热容C(t ,W)为

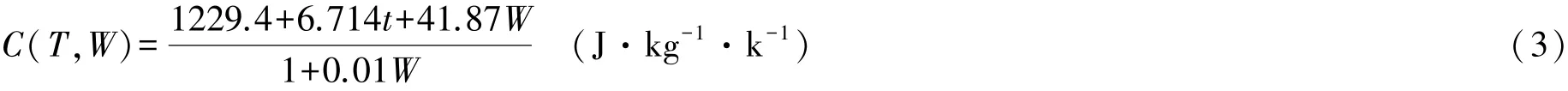
2 木材横纹导热系数理论表达式的推导

2.1 木材细胞结构模型

在分析木材生物细胞微观形态的基础上 ,作为一级近似可把细胞的微观结构看作一个中空的、细长的、方匣子模型 ,如图2所示.设细胞长度为d ,横截面是边长为b的正方形.中央是细胞腔 ,其横截面是边长为a的正方形 ,长度与细胞等长.腔内充满导热系数为λA的空气.细胞腔四周是厚为(b－a)/a的细胞壁 ,它是由导热系数为λC的木材细胞壁物质构成.

2.2 木材导热的热阻计算

由于导热与导电具有许多相似的宏观属性 ,根据类比推理方法 ,可以利用欧姆电阻公式以及电阻的串联、并联公式来计算木材的热阻.

现在考虑热流沿图2中的X方向流动的一维导热问题.由图2可以看出 ,木材在该方向的热阻R可以看作是由细胞的上下两个水平壁的热阻R1,R2与细胞腔中的空气的热阻R3并联之后再与细胞的前后两个竖直壁的热阻R4,R5串联而成 ,于是有

由图2可以看出 ,当热流从后竖直壁流向前竖直壁(X方向)时 ,必须经过上下两个水平壁和中央空气腔.由于空气的导热系数λA远小于细胞壁物质的导热系数λC,将导致热流在前后两个竖直壁中的流场呈不均匀分布状态 ,相当于热流在前后壁中经过的横截面S不再是固定的恒量S＝bd ,而是变化的截面S＝S(x) ,于是热阻的计算需要积分.为克服S(x)是未知函数给积分造成的困难 ,引入“有效截面参数e” ,用“平均”截面ebd替代原几何截面bd.从而把不均匀热阻当作均匀热阻作近似计算.结果如(4)式所示.

图2 木材细胞结构模型Fig.2 Cell structure model of wood

2.3 横纹导热系数理论表达式

根据导热与导电的类比推理 ,可以推出木材的导热系数是单位长度、单位横截面积的木材热阻的倒数.据此 ,由(4)式并代入已知数据可导出木材横纹导热系数

式中V＝a2db2d ,它是细胞中的空腔体积a2d与细胞总体积b2d的比值 ,称为木材孔隙率.木材孔隙率是未被木材的细胞壁物质和木材中的水分所占据的体积与木材总体积之比.据此这一定义可推出木材孔隙率[14 ,15]

式中ρ是为木材比重.

为确定(5)式中的待定参数e ,可利用某一已知横纹导热系数试验值的木材来确定.这里以含水率为12%、密度为900 kgűm－3的母生(Homalium hainanense)的横纹导热系数试验值等于0.1965 Wűm－1űK－1来确定.把这些已知数据分别代入(6)式和(5)式 ,便可求出e＝0.45.再把该e值代入(5)式 ,经适当整理后 ,可得木材横纹导热系数理论表达式

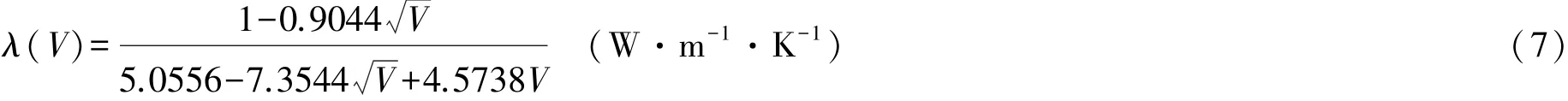
3 木材横纹导温系数理论表达式的推导

3.1 导温系数及其定义式

对于非稳态导热 ,在相同的温度梯度下 ,导热系数λ越大的物体 ,传递的热量越多 ,其内部各点温度趋于均匀分布的时间越短；而单位体积热容量ρc越小的物体 ,其内部各点温度趋于均匀分布的时间越短.换句话说 ,导热系数λ越大、单位体积热容量ρc越小的物体 ,其内部各点温度趋于均匀分布的能力越大.或者说 ,传递温度变化的能力越大.我们把表征这种传递温度变化能力的物理量称为导温系数a ,并把它定义为

3.2 木材横纹导温系数理论表达式

根据导温系数定义式(8) ,把(3)式和(7)式代入(8)式 ,易得木材横纹导温系数(10－6m－2űs－1)理论表达式

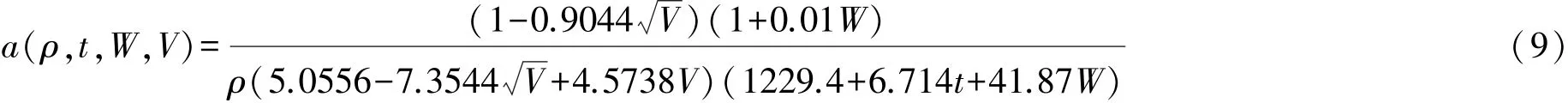
4 理论计算、试验验证与比较

4.1 比热容计算与验证和比较

应用(3)式计算28种木材的比热容 ,并与同条件下的试验值比较(表1).结果表明:28种木材比热容计算的平均误差小至2.5% ,最大误差也仅有8.0%.

应用Dunlap的经验方程式计算表1中28种木材的比热容 ,其平均误差达到9.1% ,最大误差为15.8%.应用Кириллов经验方程式做同样计算 ,其平均误差为10.4% ,最大误差则达到19.2%.若应用Кириллов的另一个经验方程式计算 ,则其平均误差为47.8% ,最大误差为52.9%.

由此可见:本文推导的木材比热容理论表达式的计算误差远比Dunlap和Кириллов经验方程式计算的误差小得多.

4.2 横纹导热系数计算与验证和比较

应用(7)式联合(6)式计算28种木材的导热系数 ,并与同条件下的试验值比较(表1).结果表明:28种木材横纹导热系数理论计算平均误差为5.7% ,最大误差为12.8%.

同时应用Maclean经验方程式和Gu-Audrey公式分别计算表1中28种木材的横纹导热系数值 ,两者的平均误差分别为15.4%和14.2% ,两者的最大误差分别达到29.7%和28.3%.

以上比较计算结果表明:本文推导的木材横纹导热系数理论表达式的计算误差远比用Maclean经验方程式和Gu-Audrey公式计算的误差小得多.

4.3 横纹导温系数理论计算与试验验证

应用(9)式计算28种木材的横纹导温系数并与同条件下的试验值比较(表1).结果表明:28种木材横纹导温系数理论计算平均误差为6.6% ,最大误差为12.5%.

5 分析与结论

(1)根据统计热力学原理推导的木材比热理论表达式具有较高的理论计算精确度.经典统计热力学有史以来只应用在单质和一些简单化合物晶体的比热容计算.本文尝试用在化学组成与结构均极其复杂的木材上 ,取得如此成功 ,是经典统计热力学在应用领域上的一个巨大拓展.

(2)依据导热与导电宏观规律的相似性 ,推出导热体热阻的计算公司用于计算木材导热热阻 ,从中导出的木材横纹导热系数理论表达式 ,经试验验证 ,其理论计算误差较小.

(3)根据导温系数的定义式 ,从木材比热容和横纹导热系数理论表达式推导木材横纹导温系数公式 ,其理论计算值与试验值比较 ,两者吻合程度令人满意.

(4)本文推导木材横纹导热系数和导温系数表达式的理论方法也适用于推导木材径向和弦向导热系数与导温系数表达式.

(5)三个热学参数的理论值与实验值基本上相符 ,使本文的研究成果不仅具有实际应用价值 ,而且因他们分别是从微观机理和宏观原理上推导所得而具有理论价值.

[1]成俊卿.木材学[M].北京:中国林业出版社 ,1985:496 ,497.

[2]高瑞堂.木材热学性质与温度关系的研究[J].东北林业大学学报 ,1985 ,13(4):24.

[3]钟云志 ,钟义山.木材导温系数模型的研究[J].西北林学院学报 ,2003 ,18(2):84－86.

[4]MACLEAN J D.Thermal conductivity of wood[J].Heating ,Piping and Air Conditioning ,1941 ,13(6):380－391.

[5]KOOLMANN F P.Principles of Wood Science and Technology[M].Berlin:Springer-verlarg ,1968:247 ,250.

[6]KELLOGG T M ,WANGAARD F F.Variation in the cell-wall density of wood[J].Wood and Fiber Science ,1969 ,1(3):180－204.

[7]SIAU J F.Transport Processes in Wood[M].New York:Springer-verlarg ,1984:132－150.

[8]ROWLEY F B ,The heat conductivity of wood at climatic temperature differences[J].Heating ,piping ,and Air Conditioning ,1993 ,5:313－323.

[9]OZISIK N M.Basic heat transfer[M].McGraw-Hill Book Company ,New York ,1997:5－65.

[10]SULEIMAN B M ,LARFELDT J B ,LECKNER B ,et al.Thermal conductivity and diffusivity of wood[J].Wood Sci Technol ,1999 ,33(6):465－473.

[11]GU H ,ZINK-SHARP A.Geometric model for softwood transverse thermal conductivity.partⅠ[J].Wood and Fiber Science ,2005 ,37(4):699－711.

[12]DUNLAP F.The specific heat of wood[M] ,Montana:Kessinger.1912.

[13]杨庆贤.木材比热的统计热力学研究[J].化学物理学报 ,1991 ,14(6):464－468.

[14]林铭 ,谢拥群 ,杨庆贤 ,等.木材热导率内在规律的理论研究[J].福建林学院学报 ,2004 ,24(1):25－27.

[15]林铭 ,陈瑞英 ,杨庆贤 ,等.木材弦向导热系数的类比法研究[J].集美大学学报:自然科学版 ,2004 ,9(4):336－340.

[16]林铭 ,饶久平 ,谢拥群 ,等.木材径向导温系数数学模型[J].福建农林大学学报:自然科学版 ,2012 ,41(3):320－323.

[17]林铭 ,谢拥群 ,饶久平 ,等.木材横纹导热系数一种新的表达式的推导及与实测值比较[J].林业科学 ,2013 ,49(2):108－111 ,49.

[18]YANG Q X.Theoretical expressions of thermal conductivity of wood[J].J Forestry Research ,2001 ,12(1):43－46.

[19]BROWNING D.L.The Chamistry of Wood[M].New York:Springer-verlarg ,1963:123－126.

[20]陈国符.植物纤维化学[M].北京:轻工业出版社 ,1984:127 ,146－148.

[21]钱学森.物理力学讲义[M].北京:科学出版社 ,1962:156 ,162.

(责任编辑:吴显达)

Derivation of a new expression for wood thermophysics parameters and comparison to experimental value

LIN Ming ,YANG Qing-xian ,RAO Jiu-ping ,XIE Yong-qun ,LIAO Yi-qiang ,WEI Wei
(College of Material Science and Engineering ,Fujian Agriculture and Forestry University ,Fuzhou ,Fujian 350002 ,China)

Theoretical equations ,derived from statistical thermodynamics and analogy ,were used to calculate specific heat ,thermal conductivity and thermal diffusivity of 28 types of wood.Then the results were compared with experimental values to verify the accu-racy of the new equations.Results showed that mean errors for above-mentioned parameters were 2.6% ,5.7%and 6.7%respective-ly ,and maximum errors were 8.0% ,12.8%and 12.5%respectively.These data were all less than results from empirical equations. Different from empirical Maclean and Gu-Audrey equations that were based on experimental results mostly ,derivation method that combines microscopic and macroscopic theories may be applied in other parameter prediction and subjects.

wood；thermal physical parameters；theoretical expression；statistical thermodynamics；analogical reasoning method

S781.37

A

1671-5470(2015)06-0646-05

10.13323/j.cnki.j.fafu(nat.sci.).2015.06.015

2015－03－11

2015－05－21

国家自然科学基金资助项目(30271057).

林铭(1963－) ,男 ,副教授 ,博士研究生.研究方向:木材科学与技术.通讯作者谢拥群(1960－) ,男 ,教授 ,博士生导师 ,研究方向:植物纤维缓冲材料的性能.Email:fjxieyq＠hotmail.com.