基于SVM的永磁同步电机直接转矩控制
杨影,韩冰,陈鑫,涂小卫
(上海大学机电工程与自动化学院,上海 200072)
基于SVM的永磁同步电机直接转矩控制
杨影,韩冰,陈鑫,涂小卫
(上海大学机电工程与自动化学院,上海 200072)
参考电压矢量的计算是基于空间矢量调制(space vector modulation,SVM)的永磁同步电机直接转矩控制的核心研究之一.从电压矢量对电磁转矩的控制作用入手,分析指出有限的电压矢量是直接转矩控制中转矩和磁链脉动大的根本原因.设计一种改进的基于空间矢量调制的直接转矩控制系统,仅仅利用定子磁链角度、转矩偏差和定子磁链偏差计算得到参考电压矢量幅值和角度.该方案计算简单,对电机参数不敏感.仿真和实验结果表明,该方法结构简单、鲁棒性强,能够明显改善直接转矩控制性能.
永磁同步电机;直接转矩控制;空间矢量调制;转矩脉动
永磁同步电机(permanent magnet synchronous motor,PMSM)直接转矩控制(direct torque control,DTC)以其对电机参数依赖程度小、转矩响应快、控制结构简单[1-2]等优点而受到广泛关注.
永磁同步电机传统DTC利用6个有效矢量控制电磁转矩和定子磁链,存在转矩脉动大、逆变器开关频率不恒定等问题,导致系统低速性能恶化[2].考虑到矢量控制中采用电压空间矢量调制方法可以获得更多的、连续变化的电压矢量,所以将开关表直接转矩控制中的滞环比较器和开关表用参考电压计算单元和空间矢量调制取代,得到一种新的控制方案——空间矢量调制直接转矩控制(space vector modulation-direct torque control,SVM-DTC).SVM的引入可以实现对电机磁链和转矩更精确的控制,从而可以有效抑制永磁同步电机直接转矩控制中的转矩和磁链脉动;引入SVM的另一个好处是开关频率固定,电流谐波分量小.因此,SVM被广泛应用于PMSM直接转矩控制系统中,以改善直接转矩控制系统的性能.实现SVM-DTC的关键之一是获得所需要的定子参考电压,国内外学者就此提出了很多方案.文献[3-5]采用基于转矩和磁链无差的SVM-DTC控制方案,虽然可以同时精确补偿定子磁链和电磁转矩偏差,但存在控制计算过于复杂、对电机参数过于依赖、系统鲁棒性差等缺陷.文献[6-8]采用转矩、磁链双环控制策略,但2个PI调节器的引入使系统结构更加复杂,参数调节也变得困难.文献[9-11]将非线性系统线性化理论应用于永磁同步电动机控制中,实现了良好的电磁转矩和磁场的解耦控制,但是精确线性化解耦对电机参数要求较高,且计算复杂.文献[12-13]采用转矩角增量控制方法,但是引入PI调节器来获得转矩角增量使得参数调节困难,鲁棒性变差.文献[14-15]采用滑膜控制、模糊控制等智能控制方法,但这些方法使得控制结构更加复杂.文献[16-18]采用新型变换器供电,如矩阵变换器、三电平变换器进行控制,但需要更加复杂的硬件条件和算法,而忽略了DTC结构简单的特点.因此,有必要研究一种简单有效的定子参考电压矢量确定方法,既可以有效减小转矩和磁链脉动,又保留直接转矩控制的结构简单和鲁棒性强的特点.
本研究提出一种改进SVM-DTC方案,避免了滞环比较器和电压矢量开关表的使用,仅仅根据电磁转矩偏差、磁链的相位和偏差,来确定参考电压矢量的幅值和相位.与其他SVMDTC方案相比,不仅保留了采用SVM的优点,又保留了传统直接转矩控制结构简单、鲁棒性强的优点.最后,对本方案和传统直接转矩控制方法进行了仿真与实验的对比.结果表明:改进的SVM-DTC方案具有良好的动态性能,且稳态性能得到改善.
1 电压矢量对电磁转矩的控制作用分析
假设忽略电动机铁心的饱和,不计电动机中的涡流和磁滞损耗,转子无阻尼绕组.在转子同步坐标系下,永磁同步电机定子电压方程可以表示为

定子磁链方程可表示为

电磁转矩可用定子电流表示为
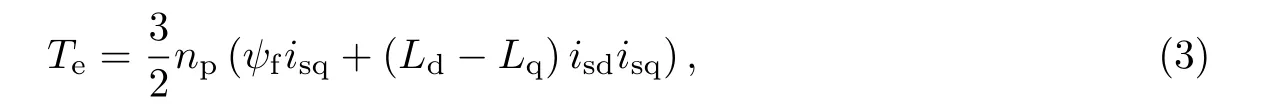
式中,ψsd,ψsq为定子磁链dq轴分量,Lsd,Lsq为定子dq轴等效电感,isd,isq为定子电流dq轴分量,ψf为转子磁链,Rs为定子绕组电阻,ωr为转子电角速度,Te为电磁转矩,np为电机极对数.
电磁转矩的变化率:
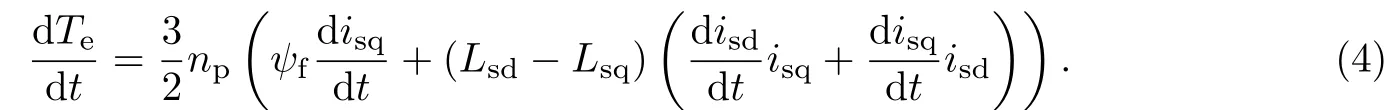
由电压方程得出dq轴电流的变化率为

将式(5)代入式(4),则电磁转矩的变化率可以表示为

式中,∆T1为给定定子电压矢量引起的电磁转矩变化率,
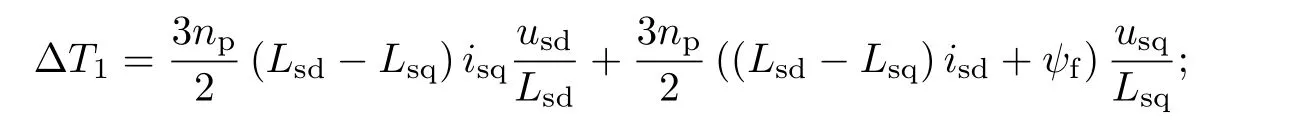
∆T2为由旋转电动势引起电流变化,进而引起的电磁转矩变化率,
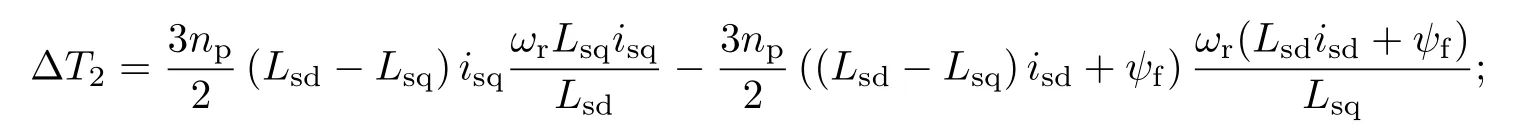
∆T3为由绕组压降引起的电磁转矩变化率,

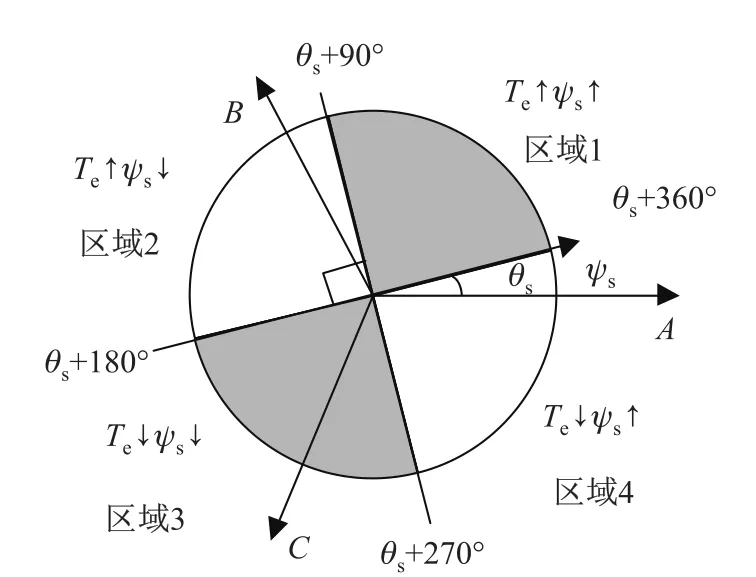
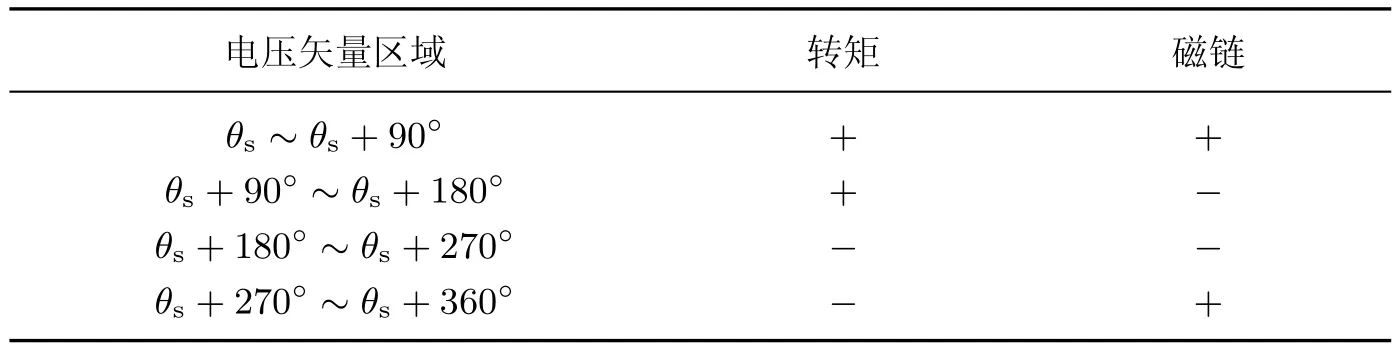
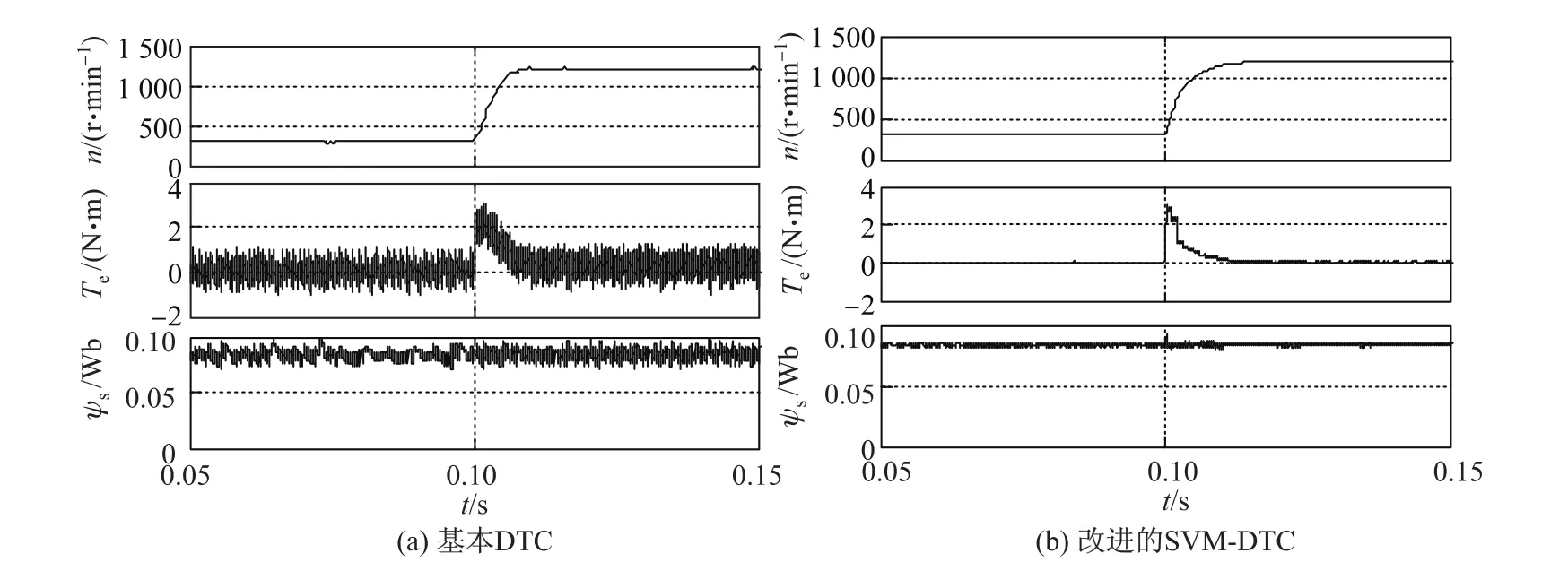
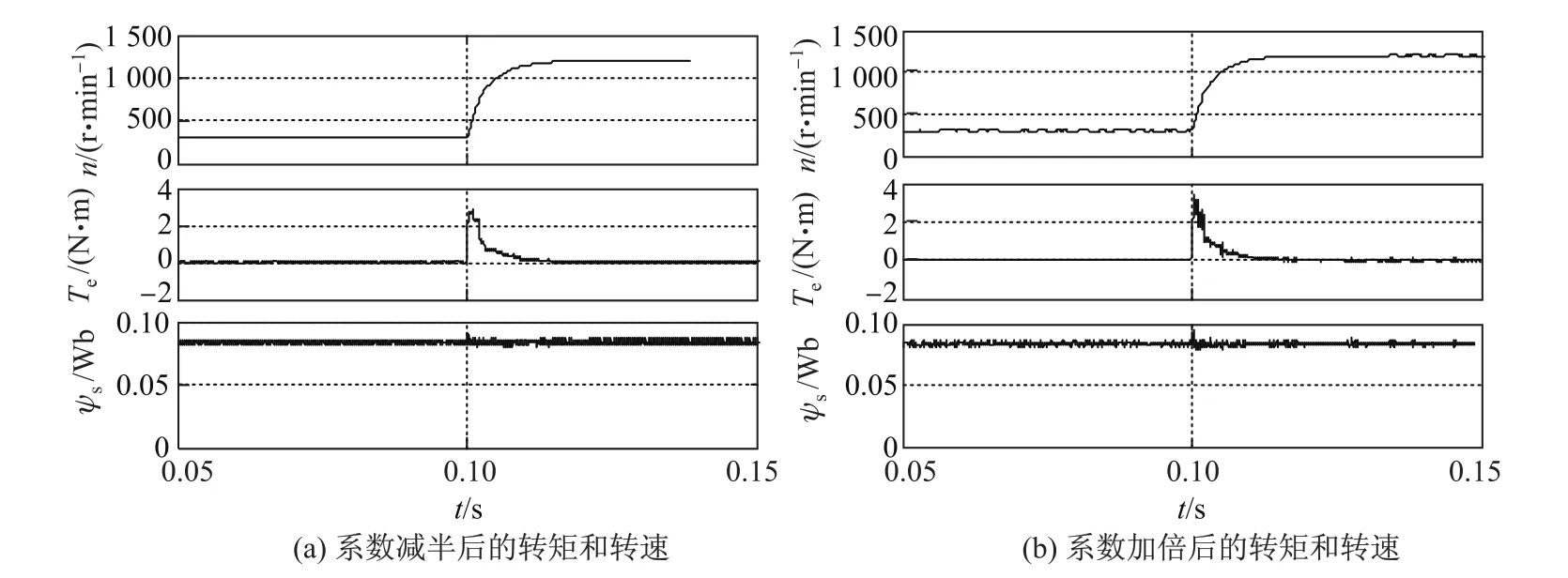
在凸极式同步电机直接转矩控制中,一般采用最大转矩/电流比控制方法来确定定子磁链给定值,有isd<0,isq>0.在d轴的旋转电动势中永磁体产生的旋转电动势占主导地位,因此ωr(Lsdisd+ψf)>0.同时,在凸极式同步电机中有Lsd 分析不同转速范围内电磁转矩的变化率可以看出: (1)∆T1取决于电压矢量dq轴电压分量的大小,当控制周期一定时,改变电压矢量长度可改变电磁转矩变化量. (2)当电机在中高速运行并施加零电压矢量时,∆T1为0,旋转电动势正比于电机转速,因此∆T2对电磁转矩变化影响较大,∆T3影响较小可以忽略.因此,电磁转矩明显减小,且电机速度越高,下降越快.为了使电磁转矩增大,dq轴电压分量需大于零,并且由于∆T2的影响,电磁转矩上升率不会太大. (3)当电机低速运行时,∆T2较小,而∆T3与负载情况有关,总体也不大.此时仅根据定子磁链所在扇区、电磁转矩控制器输出、定子磁链控制器输出选择长度一定的电压空间矢量,可能引起电磁转矩变化过快.而数字控制系统存在控制死区,因此低速时传统直接转矩控制系统转矩脉动大.综合以上分析可知,有限的电压矢量是基本DTC存在转矩和磁链脉动大的根本原因. 当电机为隐极式同步电机时,则有Lsd=Lsq,式(3)∼(6)将简化,上述结论仍然成立,因此本研究的仿真和实验中均使用隐极式同步电机. 采用SVM可以得到任意的电压矢量,因此采用SVM来获得用于控制的电压矢量,可以有效减小转矩脉动,改善系统性能.但关键是如何确定参考电压矢量的幅值和角度既可以减小转矩和磁链脉动,又不需要经过精确计算,从而保留直接转矩控制系统鲁棒性强的优点. 本研究提出一种改进的SVM-DTC方案,只需根据电磁转矩和定子磁链的偏差大小,以及定子磁链角度来分别估算参考定子电压矢量的角度和幅值,具体实现原理分析如下. 2.1 参考定子电压矢量幅值的确定 电压矢量的幅值应该根据转矩和磁链的偏差来决定.为避免复杂的电压矢量幅值计算,保持控制系统鲁棒性,利用下式计算电压矢量幅值系数: 式中,ET,Eψ分别为电磁转矩和定子磁链偏差,T∗,ψ∗分别为给定电磁转矩和定子磁链值, Te,ψs分别为估算电磁转矩和定子磁链值,KT,Kψ为正系数.最后得到参考定子电压幅值: 式中,Udc为直流母线电压. 当转矩和磁链偏差增大时,d增大,即生成的等效电压矢量幅值增大,这样可迅速减小电磁转矩和定子磁链的偏差;当转矩和磁链偏差减小时,d减小,即生成等效电压矢量幅值减小,则电磁转矩和定子磁链有微小变化,从而减小转矩和磁链脉动. 2.2 参考定子电压矢量角度的确定 为了获得更好的电机调速性能,电压矢量角度应该根据转矩和磁链偏差以及定子磁链的当前位置来决定. 如图1所示,根据当前定子磁链所在角度θs和转矩、磁链偏差符号,可确定4个电压矢量区域:(θs∼θs+90◦),(θs+90◦∼θs+180◦),(θs+180◦∼θs+270◦)和(θs+270◦∼θs+360◦). 4个区域对应转矩和磁链的关系如表1所示,“+”表示增大,“−”表示减小. 图1 改进的电压矢量区域示意图Fig.1 Schematic diagram of improved voltage vector areas 表1 电压矢量区域和转矩、磁链的关系Table 1 Relationship between voltage area,torque and flux 以区域1为例,假设定子磁链角度θs已知,转矩和磁链都增大,则选择区域1内的电压矢量.并且当转矩偏差很大(或很小)时,应选择区域1内靠近θs+90◦(或θs+0◦)位置的电压矢量;而当磁链偏差很大(或很小)时,应选择区域1内靠近θs+0◦(或θs+90◦)位置的电压矢量.也就是说,转矩偏差越大,电压矢量的角度增量越大,而定子磁链偏差越大,电压矢量的角度增量越小.为了减小电磁转矩偏差,电压矢量的角度增量 定子电压矢量的角度增量与定子磁链的偏差成反比,为了减小定子磁链偏差,电压矢量的角度增量 通过对式(9)和(10)的分析,得到如下简易的由定子磁链和转矩偏差来计算参考定子电压矢量最终角度增量的表达式: 式中,K为权重值,一般偏重转矩脉动,故选择K>0.5,φ为参考电压角度.最终得到参考定子电压矢量的角度 改进的永磁同步电机SVM-DTC系统结构如图2所示,系统获得直流母线电压、两相电流以及开关状态,通过转矩、定子磁链估算模块得到电磁转矩值和定子磁链值,以及定子磁链角度;将估算得到的转矩和磁链分别与给定转矩和磁链比较后,得到转矩偏差值和磁链偏差值;通过幅值和角度增量计算得到电压矢量幅值和角度增量;通过角度增量和定子磁链角的运算,得到电压矢量角,从而得到输出参考电压矢量;最终经过电压空间矢量调制模块输出控制电机. 图2 改进的SVM-DTC系统Fig.2 Improved SVM-DTC system 由图2可以看出,通过本方案获取参考电压矢量仅需转矩和磁链的偏差,而不需要其他电机参数,避免了复杂计算和对电机参数的依赖性,系统鲁棒性强,控制结构简单. 为了验证本研究提出的控制方案的正确性,针对永磁同步电机分别进行了仿真和实验验证.仿真和实验中所用电机参数如表2所示. 表2 电机参数Table 2 Motor parameters 3.1 仿真研究 仿真和实验验证中,取权重值K=0.6,系数KT=1,Kψ=30.图3为电机空载运行在0.1 s时,从300 r/min突变至1 200 r/min的情况下,改进的SVM-DTC和基本DTC得到的转速、电磁转矩和定子磁链波形. 图3 PMSM转速、电磁转矩、定子磁链仿真结果Fig.3 PMSM simulation results of speed,torque and flux 由图3可以看出,改进的SVM-DTC与基本DTC相比虽然动态性能稍差,但转矩和磁链脉动得到大幅降低.基本DTC的转矩在±1 N·m范围内脉动,磁链在±0.02 Wb范围内脉动,而改进的SVM-DTC转矩脉动仅为±0.1 N·m,磁链脉动仅为±0.002 Wb. 图4(a)为KT=0.5,Kψ=15条件下改进的SVM-DTC的转速和输出转矩,图4(b)为KT=2,Kψ=60条件下的转速和输出转矩.可以看出,当系数KT,Kψ在一定范围内变化时,系统仍能稳定运行,但对系统的稳态和动态响应均有一定影响.KT,Kψ越小,系统的稳态性能越好,但动态响应变慢;反之,则系统的动态响应快速,但稳态性能变差.这是因为系数越大,在同样偏差下生成的电压矢量幅值就越大,角增量也越大,对转矩和磁链的控制作用越明显,使得动态性能越好,稳态性能变差. 3.2 实验研究 图5为永磁同步电机基本DTC和改进的SVM-DTC系统在空载下,转速从300 r/min突变至1 200 r/min时的电磁转矩和转速.可以看出,改进的SVM-DTC方案仍然具有良好的动态响应特性,同时稳态性能得到明显改善. 图4 不同KT,Kψ系数下改进SVM-DTC系统仿真结果Fig.4 Simulation results of improved SVM-DTC with different KT,Kψ 图5 PMSM转速、电磁转矩、定子磁链实验结果Fig.5 PMSM experimental results of speed,torque and flux 本研究针对基于SVM的直接转矩控制提出一种新的参考电压矢量给定方案,仅需利用转矩偏差和磁链偏差计算参考电压矢量,简单易行,鲁棒性强.仿真和实验结果表明,改进的基于SVM的永磁同步电机直接转矩控制系统在保留了传统直接转矩控制结构简单、鲁棒性强、动态性能优良等优点的基础上,有效减小了转矩和磁链脉动,改善了系统性能. [1]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,2006:244-263. [2]阮毅,陈伯时.电力拖动自动控制系统-运动控制系统[M].北京:机械工业出版社,2009:192-199. [3]廖永衡,冯晓云,王珍.无差拍空间矢量调制直接转矩控制简化设计[J].电工技术学报,2011,26(6): 95-100. [4]王斌,王跃,王兆安.空间矢量调制的永磁同步电机直接转矩控制[J].电机与控制学报,2010,14(6): 45-50. [5]孙丹,贺益康.基于恒定开关频率空间矢量调制的永磁同步电机直接转矩控制[J].中国电机工程学报,2005,25(12):112-116. [6]张华强,王新生,魏鹏飞,等.基于空间矢量调制的直接转矩控制算法研究[J].电机与控制学报, 2012,16(6):13-18. [7]Gilbert F,Rahman M F.A novel speed sensorless direct torque and flux controlled interior permanent magnet synchronous motor drive[C]//Power Electronics Specialists Conference.2008: 50-56. [8]何师,邱阿瑞,袁新枚.基于SVM的永磁同步电机直接转矩控制实验研究[J].微电机,2008,41(4): 6-8. [9]周扬忠,许海军,毛洁.永磁同步发电系统中转矩和磁链精确线性化解耦控制[J].中国电机工程学报,2012,32(24):96-102. [10]刘贤兴,卜言柱,胡育文,等.基于精确线性化解耦的永磁同步电机空间矢量调制系统[J].中国电机工程学报,2007,27(30):55-59. [11]刘贤兴,胡育文,卜言柱.基于滑模变结构的永磁同步电机精确线性化控制[J].航空学报,2008, 29(5):1269-1273. [12]邱鑫,黄文新,杨建飞,等.一种基于转矩角的永磁同步电机直接转矩控制[J].中国电机工程学报, 2013,28(3):56-62. [13]王宇,邓智泉,王晓琳.基于空间矢量调制的电励磁通切换电机转矩角增量控制策略[J].中国电机工程学报,2012,32(3):75-82. [14]Chen L,Fang K L,Hu Z F.A scheme of fuzzy direct torque control for induction machine[C]//Proceedings of the Fourth International Conference on Machine Learning and Cybernetics.2005:803-807. [15]Babu P S,Ushakumari S.Modified direct torque control of induction motor drives[C]//Recent Advances in Intelligent Computational Systems.2011:937-940. [16]Guo Y,Chang X B,Chen C L.DTC-SVM-based matrix converter for a PMSM in a vessel electric propulsion system[C]//Control and Decision Conference.2009:3397-3401. [17]Cui H B,Chen C Y,Jiang W,et al.Direct torque control method of induction machines using three-level space vector modulation[C]//Power Electronics and Motion Control Conference. 2009:585-588. [18]宋文胜,冯晓云,侯黎明,等.电力牵引传动系统的三电平直接转矩控制算法的半实物实验研究[J].电工技术学报,2012,27(2):165-172. Direct torque control of permanent magnet synchronous motor based on space vector modulation control YANG Ying,HAN Bing,CHEN Xin,TU Xiao-wei To obtain the reference voltage vector is a key to the direct torque control (DTC)of permanent magnet synchronous motor(PMSM)based on the space vector modulation(SVM).From the control effect of the voltage vector on electromagnetic torque,the analysis shows that the limited number of voltage vectors is a primary cause of large ripple in the torque and flux of a DTC system.A robust DTC method of PMSM based on SVM is proposed.Amplitude and phase angle of the reference voltage vector is calculated according to the flux phase position,errors in the torque and flux,which is insensitive to motor parameters.Simulation and experimental results show that the improved DTC method based on SVM with a simple structure has strong robustness and can greatly improve the DTC performance. permanent magnet synchronous motor(PMSM);direct torque control(DTC); space vector modulation(SVM);torque ripple TM 343 A 1007-2861(2015)05-0598-08 10.3969/j.issn.1007-2861.2014.04.004 2014-04-28 杨影(1979—),女,副教授,博士,研究方向为高性能伺服控制系统.E-mail:yangying_h@163.com2 基于空间矢量调制的永磁同步电机直接转矩控制


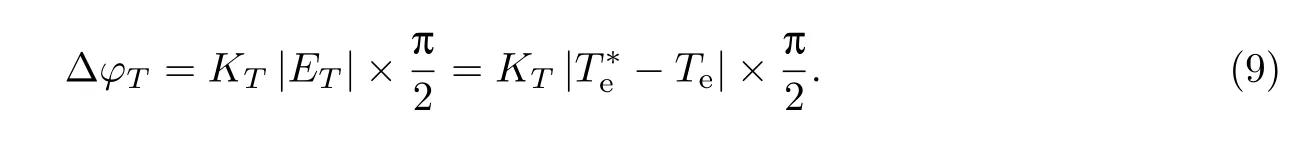
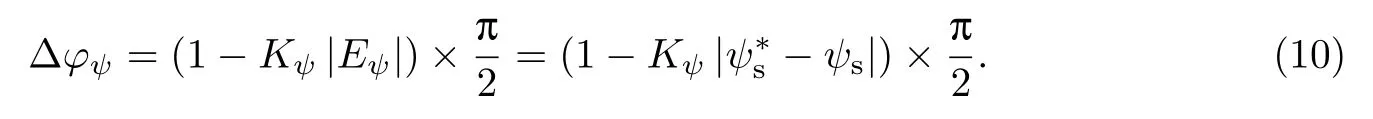
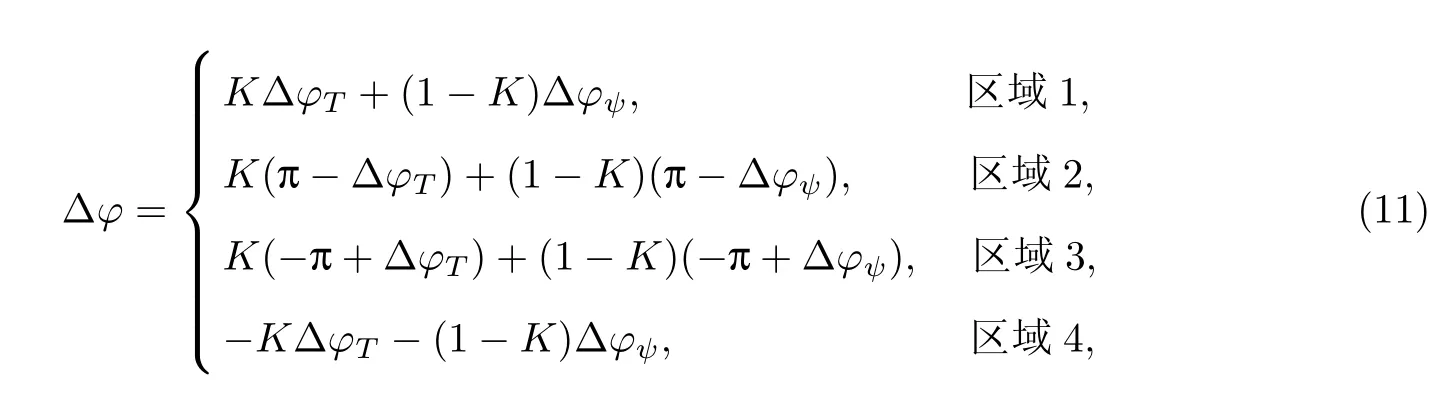


3 仿真和实验研究


4 结束语
(School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200072,China)

