斜坡浅埋基础抗拔承载力极限上限法分析

白沁园

（中国重型机械有限公司，北京100036）

1 概述

在电力、水利、公路、铁路等工程中，通常因岩土地形、地貌的限制，需要将基础埋设在坡面的顶部或坡面的中间，在线路工程中，这类基础通常称为“斜坡地基基础”。目前，有关斜坡地基基础方面的研究多集中在斜坡地基条件下基础下压承载力和下压稳定性方面。针对上述问题，国内外学者开展了大量的理论和试验研究工作，积累了丰硕的成果[1-3]。而针对斜坡地基基础上拔承载特性及承载力计算方法刚面的研究工作尚显缺乏[4-5]。其中，文献[4]给出了斜坡开挖回填正方形浅基础的上拔极限承载力的计算公式，但没有考虑基础及其上覆土体的重度，且只适用于无粘性土。文献[5]假设上拔荷载作用下，斜坡地基与平地地基破坏滑裂面的形状相同，基于M ohr-Coulm准则和极限平衡理论，推导出斜坡地基浅埋基础的抗拔承载力理论计算公式，但没考虑坡角变化对破坏滑裂面位置的影响。我国的相关规范也只给出了平地地基抗拔承载力计算方法，斜坡地基基础抗拔承载力的设计计算尚处于经验阶段。

针对上述问题，基于平地地基基础抗拔承载力计算理论，假设土体塑性滑移线呈直线性状，在此基础上，采用极限分析上限法和极限平衡理论，推导出斜坡地基浅基础上拔承载力的极限上限解计算公式，并据此确定了斜坡地基浅基础极限抗拔承载力。

2 计算模型的建立

2.1 斜坡地基浅埋扩底基础抗拔破坏机构

在上拔荷载作用下，平地地基土体的破坏模式大体分为直柱破裂面[6]、倒拔锥体破裂面[7-9]，正切曲线[10]和金字塔形曲线[11]。

假定上拔荷载作用下剪切土体滑移线为直线（图1b）。图1b中，A1A和B1B分别为两侧土体剪切滑移线，其与水平线的夹角分别为θ1和θ2；h为基础中心至斜坡面的竖直距离；bf为基础底板的宽度；b为基础主柱的宽度；β为斜坡的坡角。

图1 上拔荷载作用下斜坡地基破坏模式

根据Prandtl极限平衡理论，基础底板上方的三角形土体AOC和BOD属主动库仑区，∠CAB=∠DBA=π4+φ2（φ为土体内摩擦角）。根据平地地基抗拔机理，四边形土体D1DBB1和C1CAA1为被动库仑区。

2.2 速度相容场的建立

根据极限分析上限定理与土体极限平衡原理，构造斜坡地基土体速度相容场时，做出如下假定：①不考虑基础在上拔荷载作用下的三维效应，假定为平面应变状态[12]；②基础为完全刚性体，不考虑基础地基接触面之间的摩擦力；③地基材料为理想刚塑性体，满足相关联流动法则，且服从Mohr-Coulomb准则；④地基破坏区分为A1ACC1和D1DBB12个被动破坏区；⑤基础两侧破坏土体的水平初始速度分别为v0和v′0。根据相关联流动法则的库仑材料的性质可知，在剪切面上各点的相对速度与剪力方向成φ角[13]。基于上述假定，建立的速度相容场如图2所示。图中P1和P2分别为基础在上拔荷载作用下对土体的侧向作用力，它们与各自的滑移线外法线方向成φ角。

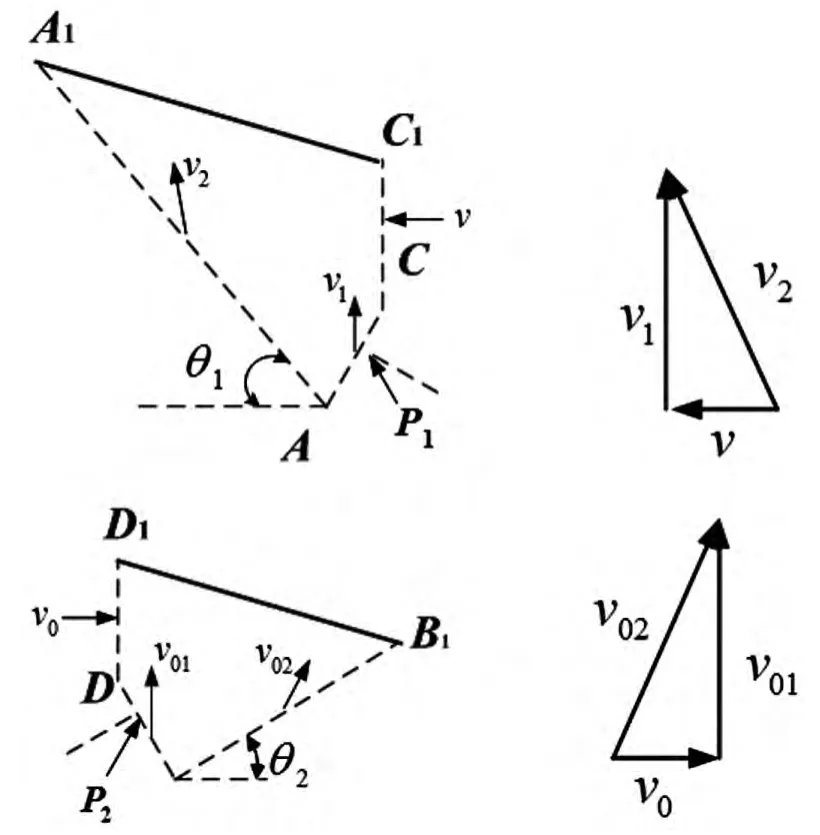
图2 基础两侧土体速度相容场

根据正弦定理，可确定各速度之间的关系式为：

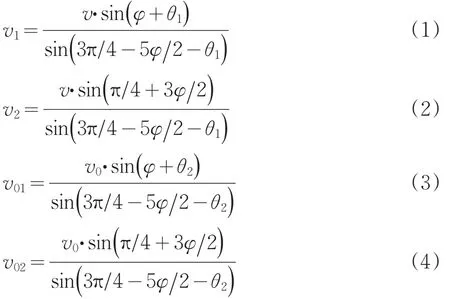
2.3 能量耗散率及重力的功率

由速度相容场假设条件，CC1和DD1上无摩擦引起的能量耗损。各间断线上的能量耗损率等于cvicosφ( )i=1,2,3与对应间断线长度的乘积，c为地基土体的粘聚强度[13]。重力的功率是指基础和破坏面范围内的土体所做的功率，是速度的垂直分量与基础和土体的重量乘积。（1）间断线AA1上的能量耗散率：

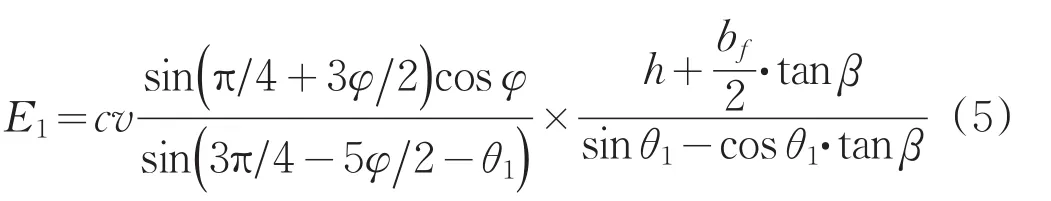
（2）间断线AC上的能量耗散率：

（3）间断线BB1上的能量耗散率：

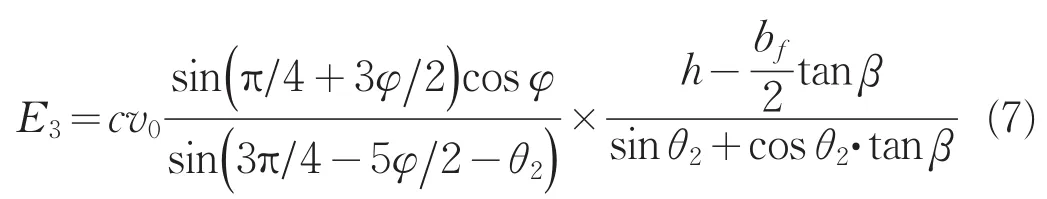
（4）间断线BD上的能量耗散率：

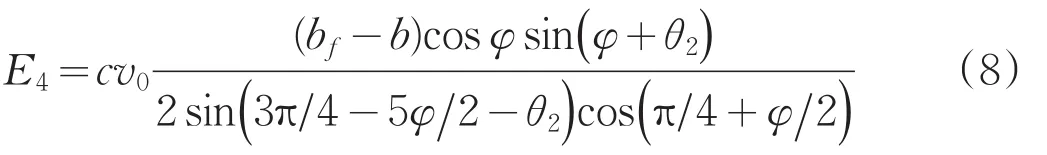
（5）土体A1ACC1所做的重力功率W1：

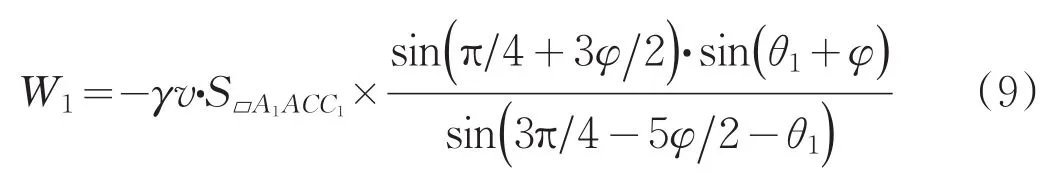
式中：

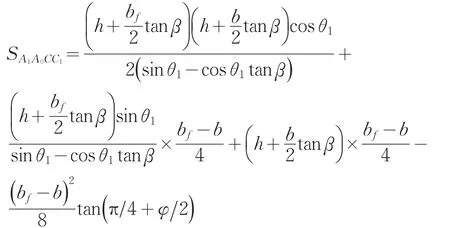
（6）土体D1DBB1所做的重力功率W2：

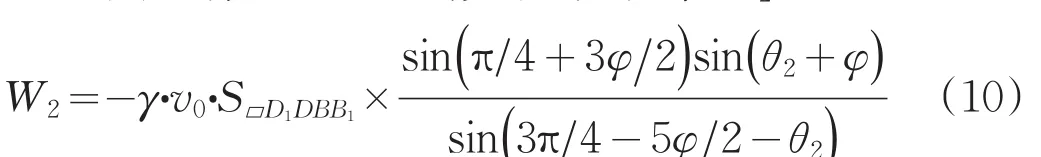
式中：

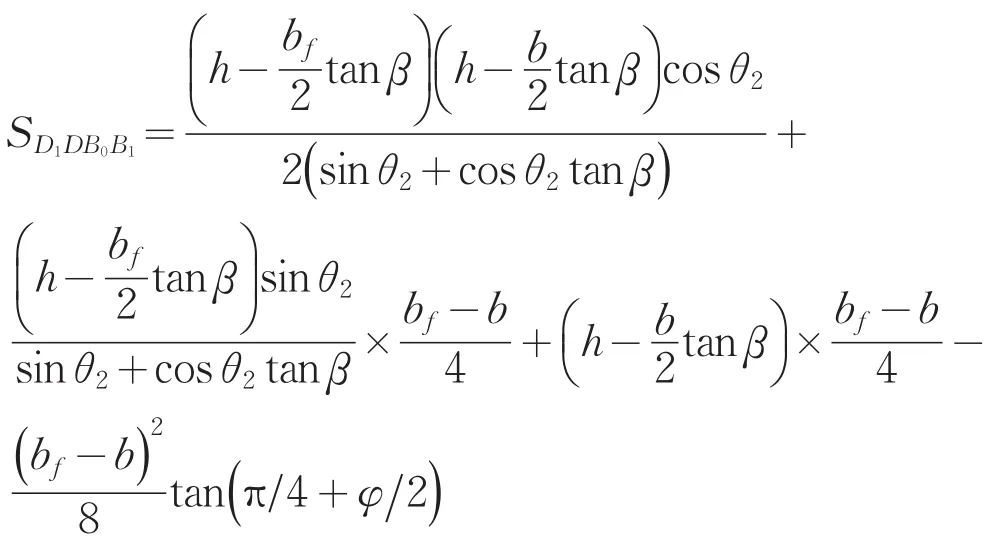
2.4 被动库仑区土体的土压力

依据斜坡地基浅基础在上拔荷载作用下达到极限状态时的相容速度场，按虚功原理建立功率方程，求出被动库仑区土体的土压力P1和P2。

由图2可知，P1和P2对土体所做的功率分别为：

分别以基础左、右侧土体为研究对象，由公式（11）推导出P1和P2表达式分别为公式（14）和（15）所示。

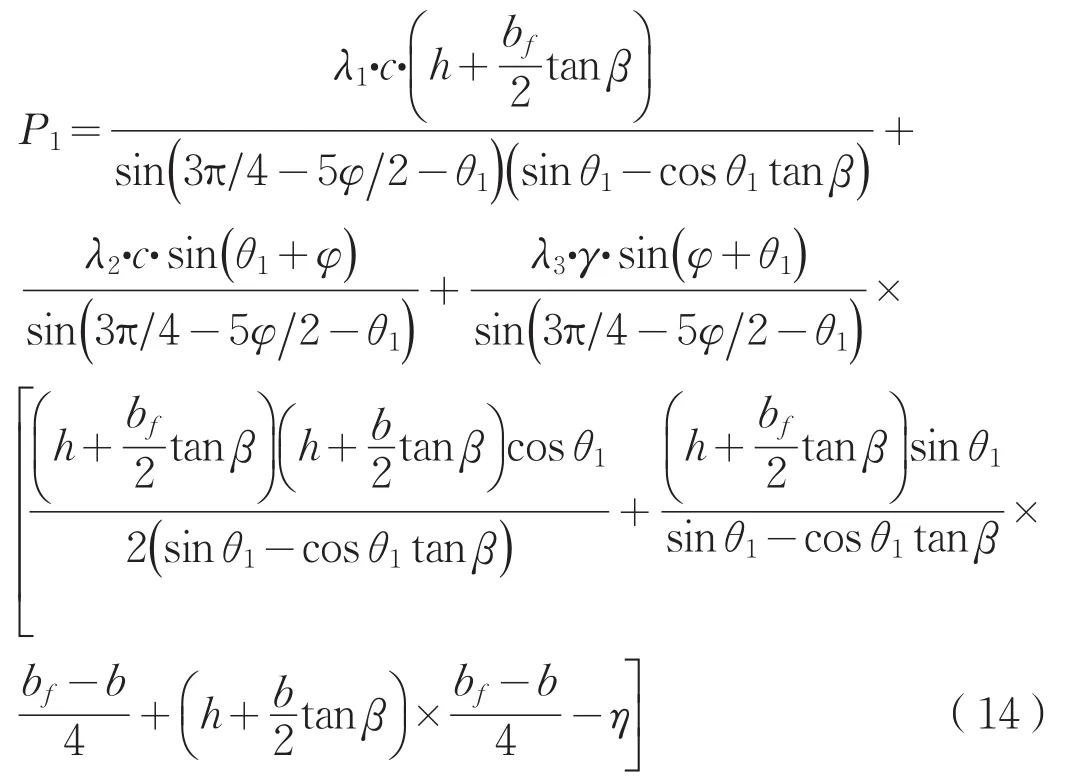
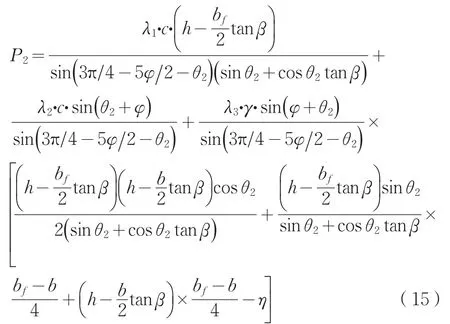
式中：

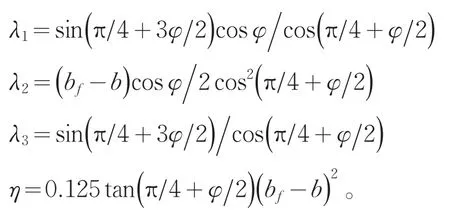
满足公式（14）和（15）的θ1和θ2值并不唯一，因此可得出一系列的P1和P2。根据极限上限法原理，满足公式（14）、（15）的最小解即为土体滑动剪切破坏时的极限值，即：P1和P2的最小上限解的条件为：

通过大量计算，结果表明：随坡角β的增加，θ1逐渐增加，而θ2则逐渐下降，即坡角的改变将引起滑移线的位置的变化。

2.5 极限上拔承载力确定

当坡前和坡后土体达到极限状态时，计算结果表明，P1≥P2，且仅在β=0时取等号。由此可见，在上拔荷载作用下，基础滑动破裂面具有不对称性，基础坡前土体先于坡后土体达到极限状态，此时对应的上拔荷载即为斜坡基础的极限抗拔承载力。以图3所示的基础及基础底板上的三角形区域土体为研究对象，当达到抗拔极限状态时，有∑Y=0，为安全起见，忽略基础及其上部三角形土体的自重，则斜坡地基浅埋扩底基础极限上拔承载力为：

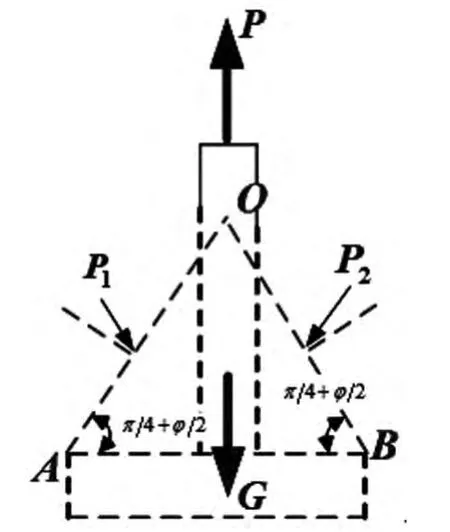
图3 极限承载力计算模型

3 结论

主要结论如下：

（1）斜坡地基浅基础在上拔荷载作用下达到极限平衡状态时，基础前后土体滑动剪切面的分布具有不对称性，且随坡角度数的变化，其位置坐标也随之发生变化。

（2）上拔荷载作用下，斜坡地基基础坡前土体较坡后土体先达到极限平衡状态，此时对应的上拔荷载即为斜地基基础的极限抗拔承载力。

[1] Narita K.Analysis of Bearing Capacity for Log-Spiral Sliding Surface[J].Soiland Foundations，1989，29(2).

[2] Saran S.，Sud V.K，and Handa S.C..Bearing Capacity of Footings Adjacent to Slopes[J].Journal of Geotechnical Engineering，ASCE，1989，115(GT4)：553-573.

[3] 尉学勇，王晓谋，贺培峰.斜坡地基极限承载力下限解计算[J].建筑科学与工程学报，2005，22(4)：77-82.

[4] E.Bazan-Zurita，D.M.Williams，J.K.Bledsoe，etc..AEP 765kV Transmission Line：Uplift Capacity of Shallow Foundations on Sloping Ground[J].Electrical Transmission Line and Substation Structures，2006：215-226.

[5] 鲁先龙，程永锋，乾增珍.输电线路斜坡地形原状土基础抗拔计算理论研究[J].电力建设，2009，30(2)：11-13.

[6] Majer P..Zur Berechnung Von Zugfundamenten[J].Osterreichische Bauzeitgschrift，1995，10(5)：85-90（in German）.

[7] Downs D.I.，Chieurzzi R..Transmission Tower Foundations[J].Journalof the Power Division，ASCE，1966，92(21)：91-114.

[8] Murray E.J.，Geddes,J.D..Uplift Behaviour of Plates in Sand[J].JournalofGeotechnical Engineering Divesion，1987，ASCE 113(3)：202-215.

[9] Clemence S.P.，Veesaert C.J..Dynamic Pullout Resistance of Anchors in Sand[C]//Proceedings of the International Conference on Soil Structure Interaction，Roorkee，India，1977：389-397.

[10] Balla A..The Resistance to Breaking Outof Mushroom Foundations for Pylons[J].Proceedings of the Fifth International Conference on Soil Mechanics and Foundation Engineering，Paris，1961：569-576.

[11] Meyerhof G.G.，Adams J.I..The Ultimate Uplift Capacity of Foundations[J].Canadian Geotechnical Journal，1968，5(4)：225-244.

[12] Minoru Matsuo.Study on the UpliftResistance of Footing(I)[J].Soiland Foundation，1967，7(4)：1-37.

[13] ChenW F著，詹世斌译.极限分析与土体塑性[M].北京：人民交通出版社，1995.