人工神经网络法在相平衡计算中的应用

曾小红

(江西省化学工业设计院，江西 南昌 330003)



人工神经网络法在相平衡计算中的应用

曾小红

(江西省化学工业设计院，江西 南昌 330003)

选用101.3kPa下的甲基二氯硅烷(1)+甲苯(2)二元体系为研究对象，用人工神经网络法来进行泡点计算。将人工神经网络法计算的泡点与实验测得的泡点作了比较，得出的平均绝对偏差与文献值比较，拟合精度更好，关联结果令人满意。

甲基二氯硅烷 甲苯 汽液平衡(VLE) 人工神经网络(ANN)

近年来，国内外一些研究人员开始尝试使用ANN来研究VLE。曾绮微等[1]建立了二元体系汽液平衡数据的人工神经网络预测模型，并以预测结果同实验结果比较，精度较高。屈强等[2]用BP神经网络预测汽液平衡常数预测。郭宁等[3]应用BP神经网络成功的关联和预测了乙醇一环己烷一水体系汽液平衡，而且其预测精度优于NRTL方程。陈维苗等[4]运用人工神经网络，对32个醇水盐体系的汽液平衡数据进行了关联，计算值与实验值符合良好，泡点温度和汽相组成的平均偏差分别是0.93K和0.015。对未列入该模型的体系的汽液平衡进行了预测，也取得了较好的结果。

本文选用101.325kPa下的甲基二氯硅烷(1)+甲苯(2)[5]二元体系为研究对象，用人工神经网络法来进行泡点计算。

1.人工神经网络概述

人工神经网络[6](Artificial Neural Network，简称ANN)是人脑的一种仿生模型，是由大量的简单处理单元(或称神经元)广泛连接而形成的复杂网络系统，按照某种拓扑结构相连接的神经模型构成。作为一种新型的黑箱方法，是近年来迅速发展起来的研究热点。ANN处理问题时不需要了解输入输出之间的相互关系，其自学习功能能够“记忆”样本所含的信息，网络根据训练样本的数据来自动寻找相互关系，给所研究的系统以具体的数学表达，从而使系统的定量、预测及优化成为可能。

自1988年由Hoskins和Himmelblau将ANN应用于化学工程中的故障诊断以来，有关ANN在化学工程中应用的发展很快。目前，ANN在化学工程中的应用领域主要有化工过程控制[7]、故障检测[8]、过程模拟[9，10]和过程优化[11，12]等。目前，在实际应用中使用最多的是BP神经网络。

2.BP神经网络

BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input layer)、隐层(hide layer)和输出层(output layer)(如图1.1所示)。

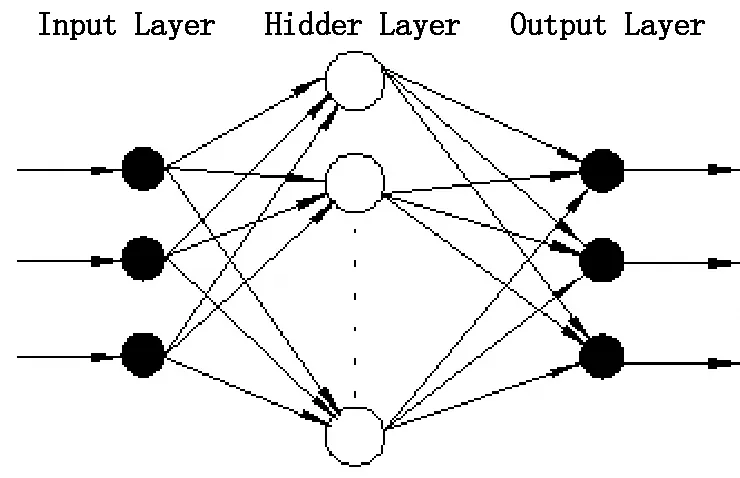
图1.1 BP神经网络结构示意图

传递函数一般为(0，1)S型变换函数：

(1.1)

输出层的神经元采用纯线形变换函数，误差函数用式1.2表示(对第P个样本)：

(1.2)

式中：tpi，Opi分别为期望输出和网络的计算输出。

3.BP网络工作原理

BP网络的学习，由四个过程组成：输入模式由输入层经隐层向输出层的“模式顺传播”过程，网络的希望输出与网络实际输出之差的误差信号由输出层经隐层向输入层逐层修正连接权的“误差逆传播”过程：由“模式顺传播”与“误差逆传播”的反复交替进行的网络“记忆训练”过程。从BP网络的学习过程可知，该算法为有教师学习算法，其学习过程可分为正向传播和反向传播两部分。在正向传播过程中，输入信息从输入层经隐层计算每一层的神经元输出并传向输出层，每一层神经元状态只影响下一层神经元的状态。如果输出值与目标的误差不符合要求，则计算出输出层的误差变化值，然后反向传播。通过网络将误差信号沿原来的传播途径反传回去，并修改各层神经元的权值和阈值，如此循环，直到达到期望输出值。BP网络的算法步骤可描述如下[13]：

第一步：采用随机函数对权值进行初始化；

第二步：输入训练集数据；

第三步：以初始的权值代入，计算实际输出；

第四步：从输出层开始，将误差信号沿连接通路反向传播，通过修正各个权值，使误差最小。

当所有样本输出值与目标期望值之间的均方差满足要求时，停止迭代，网络训练完毕，各节点的连接权值就固定下来，同时也就得到了所研究对象的输入输出之间的拓扑关系，即建立了输入向量与输出向量之间的数学定量关系。

具体步骤如图：

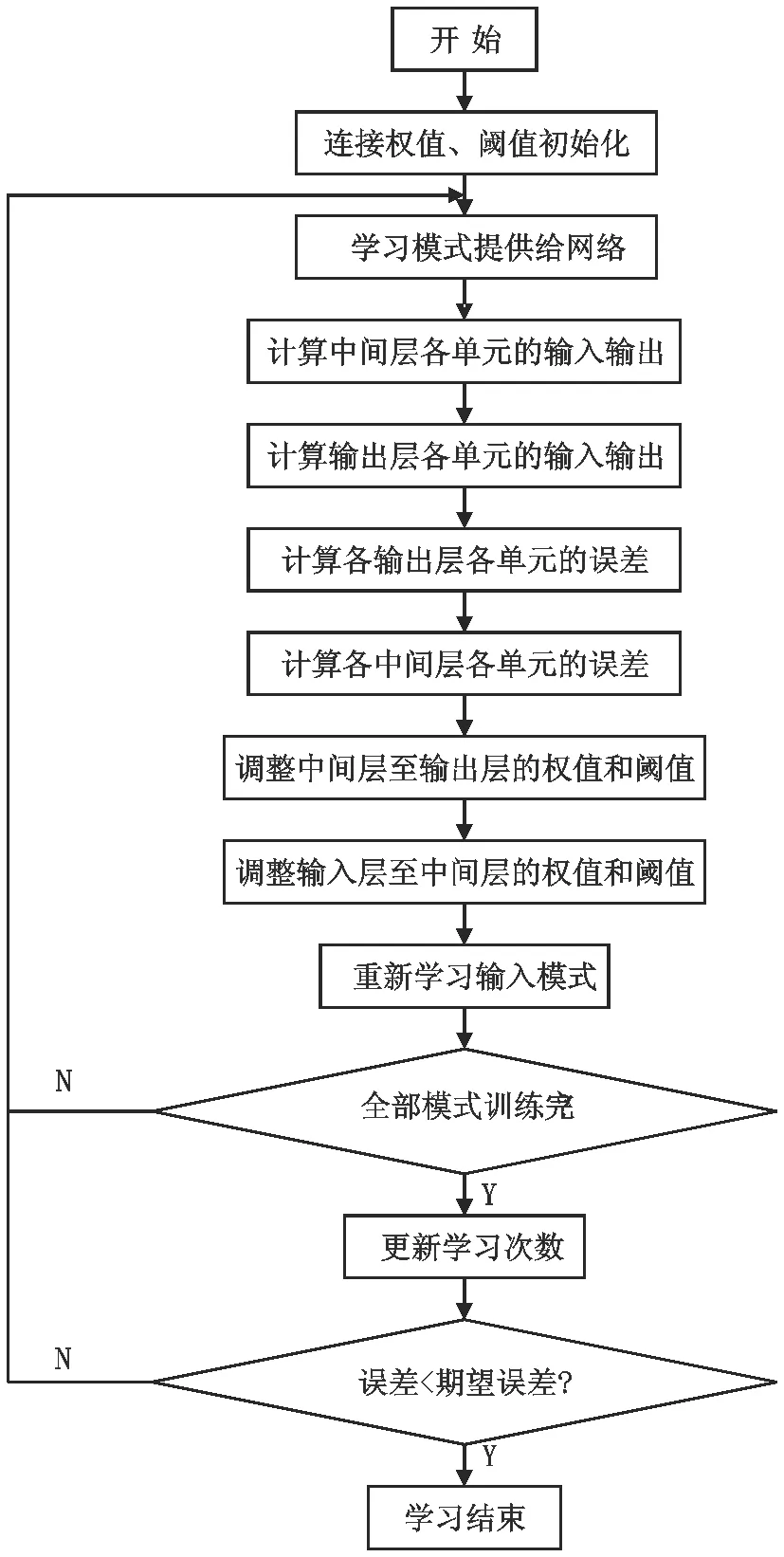
图 BP网络的算法步骤

4.BP网络设计分析

MATLAB的NNbox提供了建立神经网络的专用函数newff()。用newff函数来确定网络层数、每层中的神经元数和传递函数，其语法为：

net=newff(PR，[S1，S2，…，SN]，{TF1，TF2，…，TFN}，BTF，BLF，PF)

(1.3)

式中：PR表示由每个输入向量的最大最小值构成的Rx2矩阵；

Si表示第i层网络的神经元个数；

TFi表示第i层网络的传递函数，缺省为tansig，可选用的传递函数有tansig，logsig或purelin；

BT表示字符串变量，为网络的训练函数名，可在如下函数中选择：traingd、traingdm、traingdx、trainbfg、trainlm等，缺省为trainlm；

BLF表示字符串变量，为网络的学习函数名，缺省为learngdm；

BF表示字符串变量，为网络的性能函数，缺省为均方差‘mse’。

newff在确定网络结构后会自动调用init函数用缺省参数来初始化网络中各个权重和阈值，产生一个可训练的前馈网络，即该函数的返回值为net。

下面针对以上各参数的确定作简要介绍。

(1)网络隐含层数的选取

理论上早已证明：具有偏差和至少一个S型隐含层加上一个线性输出层的网络，能够逼近任何有理函数。增加层数主要可以进一步降低误差，提高精度，但同时也使网络复杂化，从而增加了网络权值的训练时间。而误差精度的提高实际上也可以通过增加隐含层中的神经元数目来获得，其训练效果也比增加层数更容易观察和调整，所以一般情况下，应优先考虑增加隐含层中的神经元数。因此我们从含有一个隐层的网络开始进行训练。

(2)输入层和输出层的设计

一般地，BP网络的输入变量即为待分析系统的内生变量(影响因子或自变量)数，一般根据专业知识确定。若输入变量较多，一般可通过主成份分析方法压减输入变量，也可根据剔除某一变量引起的系统误差与原系统误差的比值的大小来压减输入变量。输出变量即为系统待分析的外生变量(系统性能指标或因变量)，可以是一个，也可以是多个。一般将一个具有多个输出的网络模型转化为多个具有一个输出的网络模型效果会更好，训练也更方便。

由于BP神经网络的隐层一般采用Sigmoid转换函数，为提高训练速度和灵敏性以及有效避开Sigmoid函数的饱和区，一般要求输入数据的值在0～1之间。因此，要对输入数据进行预处理。一般要求对不同变量分别进行预处理，也可以对类似性质的变量进行统一的预处理。如果输出层节点也采用Sigmoid转换函数，输出变量也必须作相应的预处理，否则，输出变量也可以不做预处理。

预处理的方法有多种多样，各文献采用的公式也不尽相同。但必须注意的是，预处理的数据训练完成后，网络输出的结果要进行反变换才能得到实际值。再者，为保证建立的模型具有一定的外推能力，最好使数据预处理后的值在0.2～0.8之间。

(3)网络隐含层的节点选择

网络训练精度的提高，可以通过采用一个隐含层，而增加其神经元个数的方法来获得，这在结构实现上，要比增加更多的隐含层简单得多。那么究竟选取多少个隐含节点才合适?这在理论上并没有一个明确的规定。神经元的个数增多，其训练的过程越复杂，训练结果越接近期望值。但是神经元个数的选取并不是越大越好，如果神经元数目过大，将会导致训练网络过于复杂，训练时间也将增加。而且较大的神经元数目并不能保证训练结果达到期望值，因此合理选择隐层节点数非常重要。关于隐层数及其节点数的选择比较复杂，一般原则是：在能正确反映输入输出关系的基础上，应选用较少的隐层节点数，以使网络结构尽量简单。

隐层节点数的初始值可先由以下两个公式中的其中之一来确定[14，15]。

(1.4)

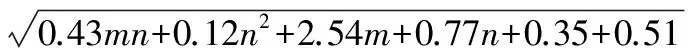
(1.5)

式中：m、n分别为输入结点数目与输出结点数目，a为1～10之间的常数。

隐层结点数可根据式(1.4)或(1.5)得出一个初始值，然后利用逐步增长(先从一个较简单的网络开始，若不符合要求则逐步增加隐层单元数到合适为止)或逐步修剪(从一个较复杂的网络开始逐步删除隐层单元)法。在具体设计时，比较实际的做法是通过对不同神经元数进行训练比较对比，然后适当地加上一点余量。

(4)网络初始权值和阈值的选取

在训练前馈神经网络之前，我们必须设置权值和阈值的初始值。当我们使用函数newff创建前馈神经网络后，网络会自动的初始化权值和阈值，缺省值是0。如果要设置这些初始值，可以使用函数init()，命令格式为：

net=init(net)

(1.6)

函数init()会自动根据网络的初始化函数以及它的参数值来设置网络权值和阈值的初始值，他们分别由参数net.initFcn和net.initParam表示。对BP神经网络来说，参数nit.initFcn的值是initwb，它使网络的初始化采用了Nguyen-Widrow算法。

(5)网络传递函数的选择

BP网络的传递函数有多种。Log-sigmoid型函数的输入值可取任意值，输出值在0和1之间；tan-sigmod型传递函数tansig的输入值可取任意值，输出值在-1到+1之间；线性传递函数purelin的输入与输出值可取任意值。BP网络通常有一个或多个隐层，该层中的神经元均采用sigmoid型传递函数，输出层的神经元则采用线性传递函数，整个网络的输出可以取任意值。只改变传递函数而其余参数均固定，训练BP网络时发现，传递函数使用tansig函数时要比logsig函数的误差小。于是在以后的训练中隐层传递函数改用tansig函数，输出层传递函数仍选用purelin函数。

(6)网络期望误差的选取

在设计网络的训练过程中，期望误差值也应当通过对比训练后确定一个合适的值，这个所谓的“合适”，是相对于所需要的隐含层的节点数来确定，因为较小的期望误差值是要靠增加隐含层的节点，以及训练时间来获得的。一般情况下，作为对比，可以同时对两个不同期望误差值的网络进行训练，最后通过综合因素的考虑来确定采用其中一个网络。结合前人研究经验，本文设期望误差为2000。

5.结果与讨论

5.1 纯物质的Antoine常数及临界性质

从文献中查得的Antoine参数及临界参数示于表5-1。

表5-1 试剂Antoine方程参数及临界参数：lg(P/KPa)=A-B/[(T/K)+C]

5.3 模型误差比较

表5-2 各种模型计算二元体系VLE的误差

注：dT=∑|Texp-Tmod|/N，dy=∑|yexp-ymod|/N，N=number of data points. *文献未提供最大绝对偏差值。

5.4 二元体系的VLE数据

BP网络模型计算二元系的汽液平衡数据关联的结果示于附表5-1，从表5-2中可看出，BP网络模型的平均绝对偏差小于文献计算的结果。

[1]曾绮微，曾颖.用人工神经网络预测二元气液平衡数据[J].福建化工，2001，4：30-31.

[2]屈强，罗金生，于广锁.人工神经网络在汽液相平衡常数预测中的应用[J].计算机与应用化学[J].18(4)：383-387.

[3]郭宁，崔志芹，云志，等.BP神经网络计算乙醇一环己烷一水体系汽一液平衡[J].南京工业大学学报，2002，24(4)：91-93.

[4]陈维苗，张雅明.神经网络技术用于醉水盐体系汽液平衡关联和预测[J].南京化工大学学报，2001，23(6)：67-70.

[5]Yu SX，Yu ZB，Qiu ZM，et al.Isobaric Vapor—liquid Equilibrium for Methyldichlorosilane-methylVinyldichlorosilane-toluene and Constituent Binary Systems[J].Chinese Journal of Chemical and Engineering，2003，11(2)：213-216.

[6]李孝安，张晓绩.神经网络与神经计算导论[M].西安：西北工业大学出版社，1994：34-362.

[7]Cooper D J，Hinde R F，Megan L A.Performance feed-back neural network for pattern-based adaptive process control[J].AIChE Annual Meeting，Chicagoll，1990.

[8]王志奎.人工神经网络在化学工程中的应用[J].现代化工，1996，9(1)：17-21.

[9]银建中，修志龙，毕明树，等.人工神经网络方法用于超临界流体萃取模拟[J].高校化学工程学报，2002，16(6)：691-695.

[10]潘海天，陈焰华，李伯耿，等.苯乙烯一马来酸配本体共聚合过程的神经网络建模[J].高校化学工程学报，2003，17(2)：195-200.

[11]张勤鑫，江涓，吴肖群，等.人工神经网络辅助丙烷氨氧化工艺条件优化设计[J].化学反应工程与工艺，1999，15(3)：282-287.

[12]周申范，黄俊.BP神经网络及其在化工优化中的应用[J].江苏化工，2000，28(4)：27-28.

[13]陈磊.人工神经网络在模式识别中的应用基础[D]，东北大学硕士学位论文，2002，8-10.

[14]徐庐生.微机神经网络[M].北京：中国医药科技出版社，1995.

[15]高大启.有教师的线性基本函数前向三层神经网络结构研究[J].计算机学报，1998，21(1)：80-85.

[16]谢心亮.多元卤代硅烷体系的汽液相平衡研究[D].南昌大学，2005.

Application ofartificial neural network in Calculating Equilibrium

ZENG Xiao-hong
(JiangxiChemicalIndustryDesignInstitute，JiangxiNanchang330003)

Choosing binary system：at 101.325kPa，Dichloromethylsilane + methylbenzene，as the study object，artificial neural network(ANN)was used to calculate bubble-point temperature and vapor composition.The mean absolute error(MAE)of artificial neural network(ANN)are less than the literature.

Dichloromethylsilane methylbenzene；vapor-liquid equilibrium(VLE)；artificial neural network(ANN)