Zr55Cu35Al10金属玻璃中紧键结合团簇的定量表征

陈刚等

摘要：定量表征金属玻璃的原子结构是深入理解和解释金属玻璃独特的物理性能和力学性能的关键.本文通过铜模吸铸法制备了Zr55Cu35Al10大块金属玻璃圆棒状试样，并利用中子衍射获得试样的对分布函数，从而定量地定义了金属玻璃紧键合团簇模型中的紧键合团簇.还通过第一性原理分子动力学模拟对Zr55Cu35Al10大块金属玻璃局域原子结构进行模拟计算，从模拟得到的结构中提取了许多紧键合团簇，并通过团簇尺寸对其定量地表征.

关键词：团簇分析；金属玻璃；紧键合团簇；第一性原理分子动力学

中图分类号：O751 文献标识码：A

Abstract：The quantitative characterization of the atomic structure of bulk metallic glass plays an important role in deeply understanding its individual physical properties and mechanical properties. Some cylindrical Zr55Cu35Al10 bulk metallic glass specimens were prepared with a suction casting in a copper mold， the pair distribution function （PDF） was obtained by neutron diffraction， and then， the tight bond cluster was defined in the present work. In addition， the local atomic structure of Zr55Cu35Al10 bulk metallic glass was simulated by ab initio molecular dynamic （AIMD）. A large number of tightbond clusters were extracted from the results and simulated in association with the quantitative characterization of sizes， which were abundant in the ideal tightbond cluster model at present.

Key words：cluster analysis；metallic glass； tightbond cluster； abinitio molecular dynamic

金属玻璃，自1960年首次合成以来，呈现出许多独特的物理性能和力学性能，成为新材料领域的研究热点[1].而其特殊且不容易被理解和表征的原子构造也吸引着大量科学工作者的研究，这些研究也是进一步开发大块非晶合金的关键点.多年来，许多结构模型被提出来用以描述金属玻璃的三维原子结构[2-4].最早的Bernal模型采用硬球无规密堆结构描述液体中原子或分子的结构，之后Cohen和Turnbull认为这种模型可以用来描述当时还是假设存在的金属玻璃原子结构[2].这种非晶原子结构模型对非晶结构的理解和对非晶的研发有很大的帮助.但是它却不能很好地解释金属玻璃的物理现象和力学性能.进入21世纪以来，密堆原子集团模型相继诞生，此模型将非晶合金的结构描述为密堆原子集团的无序排列[3-4].密堆原子集团是中程有序集团，集团内有着不同的原子排列.此模型在原子完全无序排列模型的基础上有了质的发展，为进一步从合理地解释金属玻璃的室温力学性能以及玻璃转变时伴随的物理和力学性能变化的角度深入研究金属玻璃的原子结构模型奠定了基础.

最近，基于对ZrCuAl三元系大块金属玻璃的对分布函数（Pair Distribution Function， PDF）曲线进行的系统研究，范沧教授提出了大块金属玻璃的紧键合团簇模型，该模型的核心主要包含3个部分：1） 由强化学键紧密连接的原子团簇（cluster）；2） 团簇之间的自由体积（free volume）；3）连接团簇的过渡区（interconnecting zone）[5].该模型能很好地解释许多大块金属玻璃独特的物理性能，特别是基于团簇之间的过渡区间和自由体积的转换理论，还很好地解释了在玻璃转变温度这个阈值点，金属玻璃的高屈服强度与粘体超塑性之间的转化规律[6].

金属玻璃结构中最为基本的单元：团簇结构，对团簇结构的探索无疑对金属玻璃局域原子结构的研究具有重要的意义，因此，本文选取Zr55Cu35Al10为研究对象，用Vienna Abinitio Simulation Package（VASP）软件包[7]对Zr55Cu35Al10的非晶态结构进行第一原理分子动力学（AIMD）模拟，将模拟得到的对分布函数曲线与通过中子衍射实验得到的Zr55Cu35Al10大块金属玻璃试样的实验曲线进行比较以验证模拟的有效性，进而对模拟得到结构中的紧键合团簇进行提取、表征等定量研究.

1实验方法

1.1Zr55Cu35Al10大块金属玻璃样品的制备与表征

在氩气形成的保护氛围下，高纯原材料经电弧熔炼充分后通过吸铸法至水冷铜模中充型，制成半径为3 mm，长为75 mm的圆棒状Zr55Cu35Al10 （原子百分比）大块金属玻璃试样.

用于对分布函数分析的中子衍射数据由中子粉末衍射仪收集，该衍射仪是一个高分辨率的全角衍射仪，位于美国洛斯阿拉莫斯国家实验室，Lujan中子散射中心.

对分布函数是一个在正空间，而非倒空间，分析衍射数据的方法，能得到局域原子结构的丰富信息，例如原子与毗邻原子的键长信息.其中粉末衍射数据I（Q）覆盖了较大的Q值范围（<511 nm），在这里Q=4πsinθ/λ. PDF， G（r）通过软件PDFgetN[8]将Q[S（Q）-1]进行傅里叶变换得到：

G（rk）=2/π∑Qj[S（Qj）-1]sin（Qjrk）ΔQj.（1）

1.2第一性原理分子动力学结构模拟方法

本研究模拟采用的是VASP程序，GGA交换相关泛函采用的是PW91泛函，使用投影扩充波赝势（PAW）来描述电子和离子间的相互作用.模拟过程使用正则细综来描述模拟结构.

模拟过程中，初始结构首先加热至3 000 K充分熔化，然后淬火至1 400 K并保温以模拟合金熔融态原子之间的相互作用，之后再一次淬火至室温300 K，并使用共轭梯度技术以优化构型.由于VASP程序输出的结果为所有粒子每步运动的位置坐标，用FORTRAN语言和DISCUS软件[9-10]编写相关程序，将得到的位置坐标转换为对分布函数等相关信息.

2实验结果和讨论

图1（a）为通过中子衍射实验得到的Zr55Cu35Al10大块金属玻璃的对分布函数曲线，其第一峰又被称为最近邻原子峰，包含着原子与最近邻原子的键对信息，是对分布函数曲线的关键，为讨论方便，选取其最近邻原子峰如图1（b）中实线所示.从图中可看出：图1（b）实线所示最近邻原子峰明显劈裂成两个亚峰，图中标出了第一个亚峰所处的位置，r = 27.7 nm，这说明在金属玻璃试样中有较多的原子对的结合键长在27.75 nm附近.事实上，根据文献[11]对金属玻璃紧键结合团簇模型中过渡区的定量研究，发现若将金属玻璃及晶化后的对分布函数重叠起来，两条曲线的中部存在重叠区域，研究认为该重叠区域中的ZrZr原子对只能属于紧键结合团簇，而越过该重叠区则进入过渡区，该重叠区的末端对应的键长为32.4 nm，比ZrZr原子的半径之和小约5%，从而定量地定义当原子对的键长比两原子半径之和大5%时，原子对即进入过渡区（interconnecting zone），当原子对的键长比两原子半径之和小5%时，则该原子对属于紧键结合 （tightbond）[11].由此定义可算出Zr55Cu35Al10大块金属玻璃中包含的所有原子对为紧键结合时的最大键长，如表1所示.

从表1可见，紧键结合模型所定义的最大键长，除CuCu原子对外，都大于27.7 nm（图1（b）所揭示很多原子对实际键长），也就是说，试样中较多原子对都属于所定义的紧键结合范畴，即Zr55Cu35Al10大块金属玻璃中存在较多的紧键结合原子对.

当然，紧键合团簇并非仅由一个或两个紧键结合的原子对构成，而是一个高堆垛密度、高体积应变的区域，这里不妨假设大块金属玻璃中的紧键合团簇均以某一原子为中心，同时团簇内其它原子均与中心原子紧键结合.据此假设，紧键合团簇的中心原子周围必然是极为密堆的结构，那么原子周围的密堆程度为多大时，才认为存在以该原子为中心的紧键合团簇呢？事实上，完美的晶体结构中堆垛最为紧密的FCC/HCP结构，其第一配位层内的原子数，即配位数（CN）为12.而对于玻璃结构而言，因存在类似液态结构的结构起伏，有些原子周围堆垛致密，而有些堆垛松散，所以不同原子的第一配位层内的原子数可以大于12，也可以小于12，我们有理由认为大块金属玻璃中第一配位层内的原子数不小于12的原子其周围才是密堆的，才能作为中心原子与周围的原子紧键结合而形成紧键合团簇.对分布函数曲线的最近邻原子峰显示了第一配位层的信息，由此可以从对分布函数曲线的最近邻原子峰的范围判断大块金属玻璃中原子第一配位层的范围，如图1（b）所示，选择Zr55Cu35Al10大块金属玻璃对分布函数曲线的最近邻原子峰的结尾处38.7 nm作为第一配位层的上限值.

根据上文对紧键合团簇的定义，即配位数大于12的中心原子同周围与之紧键结合的其他原子构成的原子集团.为揭示团簇原子的排列状态，必须把多个原子位置信息展现出来，本研究开展AIMD模拟，以得到的Zr55Cu35Al10玻璃结构.AIMD模拟的初始结构选择包含128个原子，具有边界周期性的立方晶胞，其中Zr，Cu，Al原子的数量分别为70，45，13，以代表Zr55Cu35Al10合金，如图2（a）所示，模拟得到的结构如图2 （b）所示，图中黑色小球代表Zr原子，灰色小球代表Cu原子，带有“Δ”符号的小球代表Al原子.利用FORTRAN语言和DICUS软件获得了AIMD模拟得到的结构中子衍射条件下的对分布函数曲线，该曲线的最近邻原子峰如图1（b）中虚线实线所示，该曲线整体上较好地拟合了实验曲线最近邻峰的峰型，虽然存在向右的“偏移”误差，但曲线所呈现的两个亚峰、最近邻原子峰也约在38.7 nm处结束等特征是令人满意的.

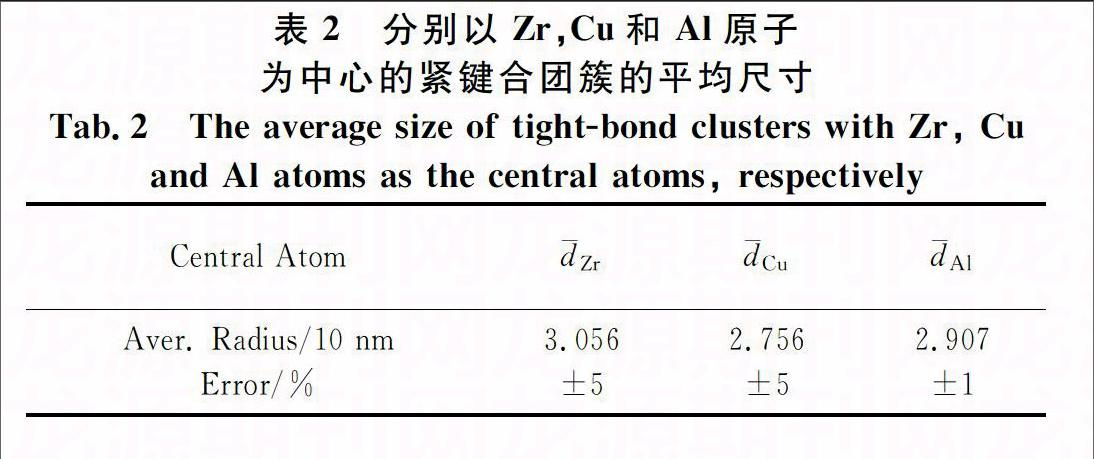
表2为以Zr，Cu，和Al原子为中心的紧键合团簇的平均尺寸，计算依据是从AIMD模拟得到的结构中提取的紧键合团簇及其所含各原子的空间坐标.这里定义团簇内各原子与团簇中心原子的平均距离为团簇的半径，即团簇的尺寸.从表2可以看出，以同类原子为中心的团簇其尺寸相差不大，而以不同类原子为中心的团簇各有其特征尺寸，这说明团簇的尺寸能够区分不同类的团簇，由Sheng等人最近提出的准等同团簇模型（the quasiequivalent cluster model）[4]认为溶质原子的偏聚程度是很低的，所有团簇都是以溶质原子为中心，周围大都是溶剂原子，所以团簇尺寸是相近的.这说明团簇尺寸的“一定量”特征是表征团簇的手段之一.

选取两个以Zr原子为中心的紧键合团簇，如图3 （a），（c）所示，为了更直观地阐述团簇尺寸的概念，先将它们投影到XOY平面，然后以团簇中心原子的投影为中心沿径向移动其它各原子的投影，使其与团簇中心原子投影的距离同三维空间中各个原子与团簇中心的距离一致，如图3 （b） ， （d） 分别是用该方法得到的（a） ，（c） 所示团簇的平面图.该平面图中，黑色圆代表是紧键合团簇的尺寸，其半径等于紧键合团簇的半径.如图3 （b）和（d）中，两紧键合团簇形状也不相同，所包含的原子数也不相同，但是其平面图内各原子“投影”均基本分布在黑色圆周之上，团簇尺寸相差不大，团簇半径分别为30.5 nm 和30.6 nm.可见，通过该方法得到的紧键合团簇平面图能有效地表征团簇的尺寸概念，更为直观，可为团簇尺寸及其结构的研究提供一种新的表征方法.

根据上文的分析，紧键合团簇尺寸大小可以作为特征参量来表征它们的结构特征，进而以此对大块金属玻璃材料的物理性能进行分析和探讨.有研究表明，在具有较强玻璃形成能力的ZrCu二元合金中添加一定量Al，所得到的ZrCuAl三元合金具有更高玻璃形成能力[12].为什么？ 本文试图以Zr原子为中心的紧键合团簇尺寸特征进行解释.事实上，AIMD模拟得到的Zr55Cu35Al10金属玻璃结构中，以Zr原子为中心的紧键合团簇占据大多数（约为73%），其余为以Cu和Al原子为中心的紧键合团簇，因此以Zr原子为中心的紧键合团簇作为影响Zr55Cu35Al10金属玻璃材料物理性能的主要因素是可以接受的.在以Zr原子为中心的紧键合团簇中，约77% 的紧键合团簇中包含1个到3个Al原子，为ZrCuAl紧键合团簇，其余均为没有包含Al原子的ZrCu紧键合团簇.AIMD模拟表明，以Zr原子为中心ZrCuAl紧键合团簇的平均半径为30.48 nm，以Zr原子为中心ZrCu紧键合团簇的平均半径为30.86 nm.可见，加入比Cu原子半径更大的Al原子，其团簇尺寸反而更小.因此可以得出，在Zr55Cu35Al10大块金属玻璃结构中，与以Zr原子为中心且不含Al原子的ZrCu紧键合团簇相比，含有1到3个Al原子的ZrCuAl紧键合团簇的堆垛更为致密，因而团簇结构也更为稳定，更为稳定的紧键合团簇使得其具备了更高的玻璃形成能力.

3结论

本文以Zr55Cu35Al10合金为研究对象，基于AIMD模拟很好地拟合了中子衍射得到径向分布函数曲线的事实，进行了大块金属玻璃的紧键合团簇模型中团簇的三维和二维结构表征的探索，得出如下结论：

1） Zr55Cu35Al10大块金属玻璃中存在大量紧键合团簇，这些紧键合团簇又以Zr原子为中心的紧键合团簇为主；

2） 同类原子为中心的团簇其尺寸大致相当，而以不同类原子为中心的团簇各有其特征尺寸；

3） 紧键合团簇尺寸大小可以作为特征参量来表征它们的结构特征，且团簇尺寸在一定程度上反映了大块金属玻璃材料的性能.

参考文献

[1]KLEMENT W， WILLENS R， DUWEZ P. Noncrystalline structure in solidified goldsilicon alloys [J]. Nature， 1960， 187： 869-870.

[2]BERNAL J D. Geometry of the structure of monatomic iiquids [J]. Nature， 1960， 185（4706）：68-70.

[3]MIRACLE D B. A structural model for metallic glasses [J]. Nature Materials， 2004， 3（10）： 697-702.

[4]SHENG H W， LUO W K， ALAMGIR F M， et al. Atomic packing and shorttomediumrange order in metallic glasses [J]. Nature， 2006， 439（7050）： 419-425.

[5]FAN C， LIAW P K， LIU C T. Atomistic model of amorphous materials [J]. Intermetallics， 2009， 17： 86-87.

[6]FAN C， REN Y， LIU C T， et al. Atomic migration and bonding characteristics during a glass transition investigated using ascast ZrCuAl [J]. Physical Review B， 2011， 83： 195-207.

[7]KRESSE G， FURTHMULLER J. Efficient iterative schemes for ab initio totalenergy calculations using a planewave basis set [J]. Physical Review B， 1996， 54（16）： 11169-11186.

[8]PETERSON P F， GUTMANN M， PROFFEN T， et al. PDFgetN： A userfriendly program to extract the total scattering structure function and the pair distribution function from neutron powder diffraction data [J]. Journal of Applied Crystallography， 2000， 33： 1192.

[9]PROFFEN T， NEDER R B. DISCUS： A program for diffuse scattering and defectstructure simulation [J]. Journal of Applied Crystallography， 1997， 30： 171-175.

[10]PROFFEN T， NEDER R B. DISCUS，A program for diffuse scattering and defect structure simulationsUpdate [J]. Journal of Applied Crystallography， 1999， 32： 838-839.

[11]FAN C， YANG X， TANG Z， et al. Interconnecting zone in metallic glasses[J]. Intermetallics， 2014， 49： 36-39.

[12]INOUE A， YAMAGUCHI H， ZHANG T， et al. AlLaCu amorphous alloys with a wide supercooled liquid region [J]. Materials Transaction JIM， 1990， 31： 104-109.