数形结合思想在中学解题中的应用

胥中胜

数形结合思想在中学解题中的应用

胥中胜

数学是研究空间形式和数量关系的科学，数和形是数学教学中的“双基”，用数形结合的思想在教学中把数和形结合起来，不但能够让一下图像形状变成数字进而进行变形，而且能使抽象的数学知识形象化，把数学题目中的一些抽象的数量关系和一些隐藏的条件关系转化为适当的几何图形，在具体的几何图形中，通过图形之间的联系和几何意义建立数量之间的联系，由此就可以达到化繁为简、变难为易的目的。

数形结合；解题；应用

数形结合思想是一种把一些文字，一些数字特点的信息用形象的形状转换出来，在数学上经常用图形的性质来说明数和文字的事实，同时又将文字和数的抽象的性质转变为形的方式。这样让数和形联系得更加紧密。在解答数学题中，应用数形结合思想方法，从图形的性质着手分析，让数学中许多抽象的概念、定理更为直观、形象使理解起来更为简单，配合代数的计算和分析的严谨使解答起来更加方便。下面我们可以从集合和绝对值问题方面来阐述数形结合思想在中学解题中的应用。

一、集合问题

在集合的运算中，通常借助数轴、韦恩图来表示，在图形上反应，并处理集合的交、并、补等集合运算，使问题在图形上直观的反应出来，使问题得以简化，这样让运算变得快捷。

例：某年级先后举办了数学、历史、音乐的讲座，其中有75人听了数学讲座，68人听了历史讲座，61人听了音乐讲座，17人同时听了数学、历史讲座，12人同时听了数学、音乐讲座，9人同时听了历史音乐、讲座，还有6人听了全部讲座，求听讲座的人数。

分析：由于75人听了数学讲座，68人听了历史讲座，61人听了音乐讲座，则这三个组共有75+68+61人，17人同时听了数学、历史讲座，12人同时听了数学、音乐讲座，9人同时听了历史、音乐讲座，还有6人听了全部讲座，根据容斥原理可知，听讲座的共有68+75+61-（17+12+9）+6人。

解：68+75+61-（17+12+9）+6=204-38+6=172.

所以，听讲座的人数为：172人。

在本例的求解中回避了抽象分析的思路,根据韦恩图我们很容易直观的发现题意中所隐藏的等量关系,从而此问题变可以迎刃而解。

小结:运用韦恩图在解答集合题上,实质则是将用文字和数字表达的集合含义转化为用图形语言来阐述,这样显得更为直观，才不会被题中的含义绕晕，这就是数形结合数学思想方法的具体体现。在解答这类问题中运用好韦恩图可以提高解题的速度和提高数学思维的能力。

二、绝对值问题

例：已知实数a,b的位置如图所示，以下计算正确的是（ ）

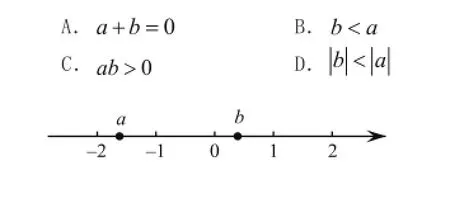
分析：此题考查了实数的大小比较，绝对值与数轴等知识，解题的关键是数形结合思想的运用，能正确判断实数 的正负以及绝对值大小．

解：根据图形可知：∵a在b的左边，∴a ＜b，∴选项B错误；∵a与b符号相反，且a到原点的距离大于b到原点的距离，∴a＋b＜0，ab ＜0，与b符号相反，且a到原形是数学的重要组成部，∴选项A与C错误，选项D正确，故选D．

在数学教学中数和形是数学的重要组成部分，是提高数学思维能力和培养数学修养的重要因素。在中学阶段不仅是要培养学生的解题能力更重要的是培养学生的思维能力及发展学生的智力，把数字形象化这样有利于开发学生想象思维，提高学生的智力的突破口。学生数学能力的差异主要是通过数学思维的灵活性、深刻性，敏捷性等方式来体现，数形结合有利于培养学生思维的灵活性和深刻性。因此在中学教学中，数形结合不仅是一种解题方法，又是一种培养学生的基础的、不可缺少的数学思想。将数形结合方法运用到解答中主要体现在两个方面：一方面是是将题目中的数据，条件，关系转变为相应的图形，通过图形更直观的分析题中需要解决的问题，分析其几何意义；另一方面：则是将一些图形转变为相应的函数关系、限制条件，通过数字进行相应的变距离，∴a＋b＜0，ab力和培养数学修养的重仅是要培养学生的解题生的思维能力及发展学化这样有利于开发学生智力的突破口。学生数过数学思维的灵活性、来体现，数形结合有利活性和深刻性。因此在不仅是一种解题方法，础的、不可缺少的数学运用到解答中主要体现是将题目中的数据，条图形，通过图形更直观一些图形转变为相应的通过数字进行相应的变C错误，选项D正确，故问题，分析其几何意换得到处理。二者都是数形结合，不可单看一方面。

由于数形结合的特点，在数学教学中要求教师在长期的教学过程中潜移默化的让学生掌握，而不仅仅是依靠几节课专门针对数形结合解题方法来讲解例子，因为这样是不能让学生真正理解和掌握数形结合思想方法的。

[1]陈婉华.在数学教学中提高学生的多种能力[J].青年探索,2005,(06).

[2]董涛.建构主义视野中的数学概念教学[J]曲阜师范大学学报(自然科学版),2004,(02).

[3]施献慧.数形结合思想在数学解题中的应J].云南教育，2003，（35）.

[4]卢丙仁.数形结合的思想方法在函数教学应用[J].开封教育学院学报，2003，（04）.

[5]刘焕芳.巧用数学结合思想解题[J].数学，2005，（01）.

(作者单位：四川平昌县尖山小学)