弹道中段群目标平动补偿与分离方法
胡晓伟童宁宁董会旭初洪帅
①(空军工程大学防空反导学院 西安 710051)
②(95920部队 沧州 253801)
弹道中段群目标平动补偿与分离方法
胡晓伟*①童宁宁①董会旭①初洪帅②
①(空军工程大学防空反导学院 西安 710051)
②(95920部队 沧州 253801)
弹道微动群目标时频图是多目标多散射点微多普勒的叠加,以往针对单目标的补偿与分离方法不再适用。针对这一问题,该文首先分析了群目标及诱饵的微多普勒形式;利用弹道中段目标运动平稳,短时观测加速度近似为常数的特性,采用Radon变换检测微多普勒曲线的倾斜程度,用最小熵准则和高斯函数拟合的方法估计平动参数,进而完成平动补偿;对补偿后的群目标时频图利用Viterbi算法提取各条微多普勒曲线,依据同一目标各散射点微多普勒的周期相关性,完成群目标分离;最后仿真验证了以上方法的有效性。
弹道目标;微多普勒;平动补偿;Radon变换;群目标分离
1 引言
弹道目标分类与识别是弹道导弹防御中极为重要的一个环节。利用目标的微动特性[13]-进行弹道目标识别是一种可行的方法。目前国内外在弹道微动目标方面已进行了大量研究,提出了基于多目标跟踪技术、经验模式分解、Chirplet分解等多种微多普勒分离与特征提取方法,并验证了这些方法的有效性[47]-。以上研究针对的都是空间可分离的单目标,而实际当中防御方需要面对的往往是由弹头和诱饵组成的在空间上不可分辨的群目标,这时的目标时频图将由多目标多散射点的微动曲线叠加而成,现有的针对单目标的分析方法将不再适用。
针对微动群目标,文献[8]提出利用自适应Chirplet变换进行群目标信号拟合得到每个目标主要微动频率分量,再利用Hough变换检测直线数量来判定群目标个数;文献[9]将B分布和Viterbi算法进行有机结合,提取多目标微多普勒特征,进而对多目标进行分辨。以上研究都基于同一个假设即群目标中每一个目标只有一个强散射点,而这与实际情况不相符;存在的另一个不足是都没有考虑目标平动补偿的问题。平动补偿是微动目标特征提取与分类识别的前提,对于单目标的平动补偿,已进行了很多研究[5,10,11]。但关于群目标的平动补偿还没有相关方面的报道。弹道目标在中段飞行较为平稳,可近似为二阶多项式[10],因此平动将使得群目标微多普勒在时频域呈线性倾斜。基于这一特性,本文提出采用Radon变换来检测微多普勒曲线的倾斜程度,利用最小熵准则和高斯拟合的方法估计平动参数,进而完成平动补偿;对平动补偿后的时频图,利用Viterbi算法进行微多普勒提取,最后依据同一目标微动周期的相关性实现群目标的分离。
2 群目标微多普勒分析
在弹道群目标中,除了弹头外还可能存在轻重诱饵、弹体碎片等多种目标。这些弹道目标最显著的差异就是其微动形式不同[12,13]。弹头由于自旋定向的需要,会保持进动;重诱饵因为没有姿态控制会处于摇摆状态;对于各轻诱饵和碎片则会随机翻滚。下面就以进动弹头和摆动重诱饵为例分析其微动形式和微多普勒。
2.1 弹头微多普勒
如图1所示是一锥体弹头的微动模型。参考坐标系O-XYZ与雷达坐标系平行,目标在雷达坐标系中的方位角和俯仰角分别为0,β;弹体坐标系O-xyz以目标对称轴为y轴,初始时刻y轴在参考坐标系中的偏航角、俯仰角和横滚角分别为0,sβ, 0;进动坐标系O-xpypzp以目标进动轴为yp轴,初始时刻yp轴在参考坐标系中的偏航角、俯仰角和横滚角分别为0,pβ, 0;雷达视线(LOS)在参考坐标系下的单位方向矢量为

进动轴在参考坐标系下的单位方向矢量为:

首先对于理想散射点–锥顶P0,由于具有旋转对称结构,目标绕对称轴的旋转具有不变性,故只需考虑目标进动。设P0在弹体坐标系中的位置矢量为r0=(0, y0, 0)T,以角速度Ω绕进动轴旋转。文献[14]推导了经过时间t后点P0的微多普勒(λ为波长):

图1 弹头的进动模型
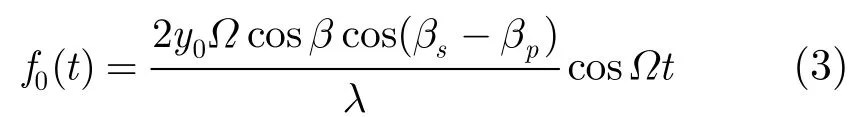
锥体弹头的散射中心除锥顶外,其它散射中心是雷达视线和目标对称轴形成的平面与底部平面边缘的交点[15],即图1中P1, P2点。它们的运动规律与目标上理想散射点的进动规律并不相同,属于滑动散射点。经t时刻后滑动散射点的微多普勒形式为[14]
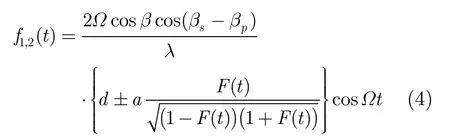
2.2 诱饵微多普勒
图2为锥体诱饵的摆动模型。参考坐标系O-XYZ与雷达坐标系平行,目标在雷达坐标系中的方位角和俯仰角分别为0, β;弹体坐标系O-xyz以目标对称轴为y轴,初始时刻y轴在参考坐标系中的偏航角、俯仰角和横滚角分别为0, βs, 0;雷达视线(LOS)在参考坐标系下的单位方向矢量为;给定方向矢量OC,诱饵以O点为中心在OC与Oy所确定的平面yOC内摆动,摆动角的变化规律为θ(t )=θssinωst 。
设诱饵上一散射点P(位于XOY平面)在弹体坐标系中的初始位置矢量rp=(xP0,yP0,0)T,在参考坐标系中矢量OP=RirP, Ri为表征诱饵初始姿态的Euler旋转矩阵;t时刻P点在参考坐标系中的位置矢量为r(t)=R(t)rP。R(t)为t时刻的Euler旋转矩阵,此时弹体坐标系在参考坐标系中的偏航角、俯仰角和横滚角分别为0, βs(t ), 0,其中βs(t)=βs-θssinωst。
则t时刻P点的径向距离为
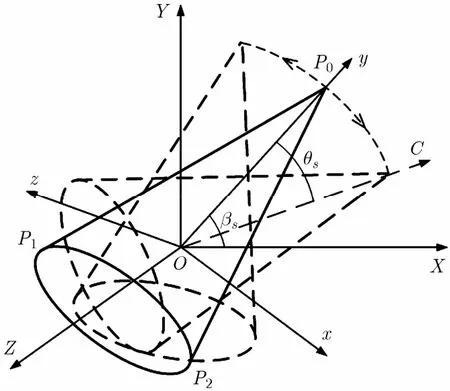
图2 锥体诱饵的摆动模型
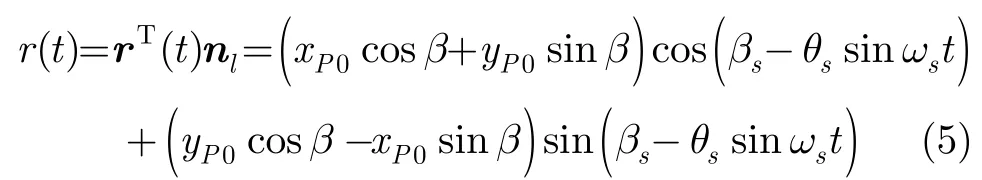
可以得到P点的微多普勒为

由于在摆动模型下,锥体诱饵不存在相对雷达的滑动散射点,故其上的等效散射中心(P0, P1, P2)均满足以上微多普勒形式。
3 基于TFD-Radon变换的群目标平动补偿
假设雷达发射波长为λ的单频信号,接收到的群目标的基频回波信号为
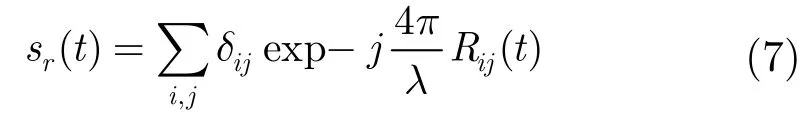
其中δij为群目标中第i个目标上第j个散射点的散射系数, Rij(t)为t时刻该点与雷达的径向距离。
弹道目标中段运动比较平稳,平动距离可近似为二阶多项式:

其中R0,v,a分别为目标群t时刻的径向距离、速度和加速度,rij(t)为该点的微动距离。

微多普勒为信号相位的一阶导数,因此群目标微多普勒可表示为
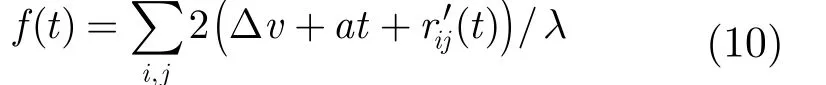
由式(10)可以看到群目标时频域由多个目标的多个散射点的微多普勒叠加而成,由于各瞬时频率相互影响,使得精确估计每个瞬时频率较为困难。但平动导致群目标微动曲线整体上呈线性分布,且线性程度由平动参数vΔ和a决定。考虑群目标时频域的分布特点,本文采用Radon变换进行平动补偿。
Radon变换[16]是一种通过积分计算图像在某个方向投影的图像特征提取方法。2R中连续2维函数(,)gxy的Radon变换为

式(11)中,D为积分图像平面,ρ为坐标原点到直线的距离,δ为dirac-delta函数,g(x,y)为点(x,y)的强度。当(ρ,θ)给定时,式(11)表示了g(x,y)在直线ρ=xcosθ+y sinθ上的线积分。
对群目标时频图进行Radon变换,时频面多普勒的线性分布将映射成(,)ρθ平面上的一个亮点,通过检测亮点的峰值位置就可以估计目标的平动参数。
因为群目标时频图是由多条服从同一线性分布的曲线叠加而成,并不是严格的一条直线,这会导致在变换域上对应的亮点散焦,从而影响平动参数估计的精度。为此本文利用最小熵准则和高斯函数拟合的方法估计平动参数。定义熵:

4 基于周期相关性的群目标分离
经过平动补偿后,群目标时频图将聚集在零频附近,此时就可提取目标微多普勒进而分离群目标。这里采用信号隐状态估计的有效方法Viterbi算法[10]来估计瞬时频率,瞬时频率估计路径最小化的表达式为

利用Viterbi算法可以依次抽取时频图中的各条微动曲线。为分离不同目标,下面对群目标微多普勒周期性进行分析。
对于弹头,由式(3),式(4)可知,锥顶散射点微多普勒服从周期为2π/Ω的正弦变化,即f0(t)=f0(t+2π/Ω);底面滑动散射点的微多普勒变化形式复杂,但同样满足f1,2(t)=f1,2(t+2π/Ω)。由式(6)可知,诱饵上不同散射点微多普勒形式不同,但有同样的周期性,即f(t)=f(t+2π/ωs)。通过以上分析可以得出结论:同一目标不同散射点微多普勒之间存在周期相关性,并且这种周期性是由目标整体的微动周期决定;而不同目标各散射点之间不存这种相关性。因此可以利用群目标的这一特性将不同目标进行分离。
综上,设计弹道群目标的分离算法流程为:
(1)利用雷达测量值对群目标回波进行预补偿,得到预补偿回波信号sr(t);
(2)对sr(t)进行时频变换,获得群目标的时频图g(t,f);
(3)对g(t,f)进行Radon变换,得到2维平面函数R(ρ,θ);
(5)对平动补偿后的回波再次进行时频变换,利用Viterbi算法依次抽取时频图中的各条微动曲线;
(6) 对各条微动曲线作FFT,分析其频谱低频成分确定各微动曲线的周期,最后利用目标周期的相关性,对群目标进行分离。
5 仿真实验
为验证本文方法的有效性,进行以下仿真实验。
设导弹关机点高度为250 km,关机点速度为4.55 km/s,在地心直角坐标中的速度方向单位矢量为[-0.5,3/2,0]。弹头在200 s时释放诱饵,设目标群由一个锥体弹头和两个等比例锥体诱饵组成,锥体直径为3 m,底面半径为1 m,质心在轴线距底面1 m处。弹头和诱饵在同一个雷达波束内,且平动速度相同。弹头进动频率为1 Hz,进动角为10°;诱饵1摆动频率为1.5 Hz,幅度为20°;诱饵2摆动频率为2 Hz,幅度为25°。
图3仿真了导弹在地心直角坐标系下的弹道轨迹,从关机点到再入点共用时约1000 s。选择200~205 s作为观测时段,图4仿真了观测时段内弹头和诱饵锥顶散射点的径向速度变化,从中可以看到:(1)微动使得散射点速度发生规律性变化,不同散射点的速度变化规律存在差异;(2)在观测时段内所有散射点速度曲线随时间作同方向的偏移,并且近似为线性规律。
设置雷达工作频率为3 GHz,重复频率为1000 Hz,仿真群目标回波。对预补偿后的回波利用Gabor变换进行时频分析,得到群目标的时频图如图5所示。
可以直观地看到,群目标时频图由5条不同变化规律的微多普勒曲线叠加而成,这是由于雷达的观测视角使得弹头和诱饵各有1个散射点被遮挡。同时诱饵2的底面滑动散射点由于散射强度较弱,经时频变换后在时频图上几乎不可见。
为说明本文补偿方法对处理群目标的优势,首先应用文献[9]的方法提取图5中最强点的微多普勒,结果如图6所示。从图6中可以看到,由于不同目标散射点微多普勒的相互影响,使得用文献[9]的方法提取的微多普勒已不能反映目标的平动规律,即该方法对群目标的平动补偿是失效的。
下面应用本文的补偿方法对群目标时频图进行Radon变换,结果如图7所示。

图3 地心直角坐标系下中段弹道轨迹

图4 弹头、诱饵锥顶散射点径向速度

图5 预补偿后回波时频变换结果

图6 文献[9]方法提取的最强点微多普勒

图7 群目标时频图Radon变换
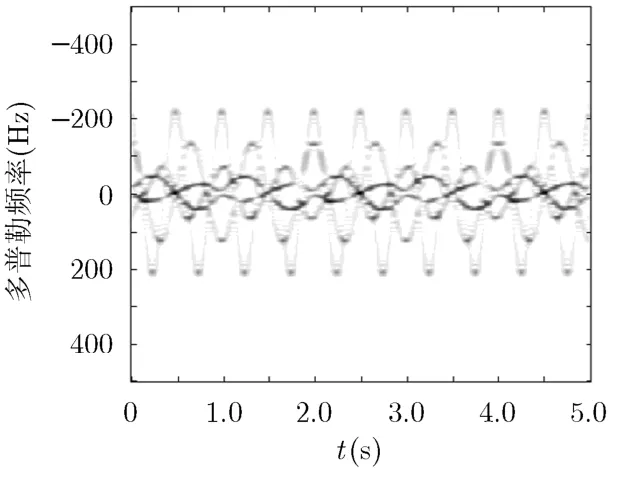
图8 补偿后回波时频变换结果
利用Viterbi算法从以上时频图中依次抽取5条曲线,如图9所示,可以看到抽取的曲线基本能够反映多普勒的变化规律。为了平滑曲线,利用二阶Fourier样条对曲线进行拟合,结果如图10所示。
对平滑后的曲线进行FFT,剔除零频干扰后结果如图11所示。从图11中可以看到,曲线1,曲线2均在f1=1 Hz处出现峰值,说明其对应的散射点微多普勒曲线具有相同的周期1/f1,因此可以将其划归一类目标1;同样,曲线3,曲线4在f2≈1.5 Hz处出现峰值,说明其对应的散射点微多普勒曲线周期为1/f2,因此将其划归目标2;对于曲线5在f3≈2 Hz处出现峰值,说明其对应的散射点微多普勒曲线周期均为1/f3,因此将其划归目标3。综上,可以得出结论:在群目标中共有3个目标,并且其微动主周期分别为1/f1, 1/f2和1/f3。该结论与设置的仿真条件–弹头进动频率1 Hz,诱饵1摆动频率1.5 Hz,诱饵2摆动频率2 Hz相吻合,说明了结果的正确性。
6 结束语
群目标时频图是多个微动分量的叠加,想要从中提取单一分量来进行平动补偿比较困难。本文采用的TFD-Radon补偿方法检测的是整体的平动趋势,而不用提取单一分量,因此较为容易实现。仿真验证了高信噪比时本文方法具有良好的平动补偿与分离效果。
在低信噪比的条件下,由于Radon变换检测的是时频图的整体线性特性,受噪声影响小,因此在低信噪比时也能很好地实现平动补偿;而Viterbi算法进行多分量抽取时,要求各分量具有良好的连续性,如果受到强噪声的影响,可能抽取效果不理想,进而影响群目标的分离。这里设想一种思路:利用整体特征对噪声不敏感的优点,考虑如果能够利用时频图的某种整体特性,如时间上的周期相关性,通过某种方法提取这种周期特征,就可以实现不同微动周期目标在低信噪比条件下的分离。

图9 Viterbi算法抽取的微多普勒曲线

图10 平滑后的微多普勒曲线
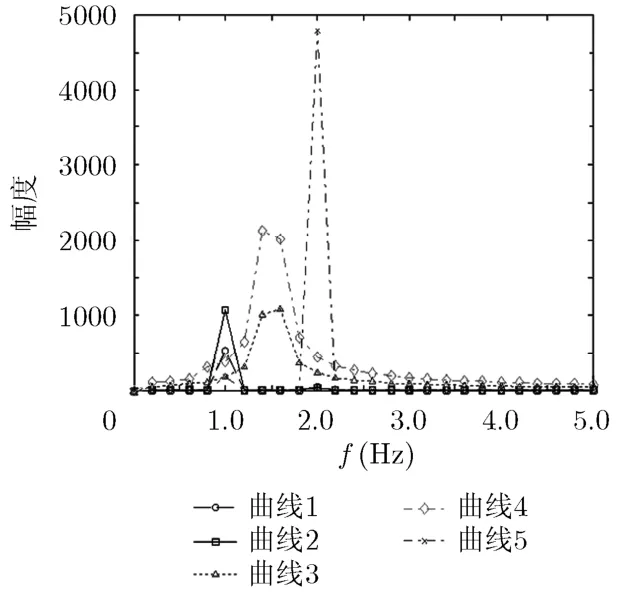
图11 平滑后曲线的FFT结果
[1] Chen V C, Li F Y, Ho S S, et al.. Analysis of micro-Doppler signatures[J]. IEE Proceedings on Radar, Sonar and Navigation, 2003, 150(4): 271-276.
[2] 李彦兵, 杜兰, 刘宏伟, 等. 基于微多普勒效应和多级小波分解的轮式履带式车辆分类研究[J]. 电子与信息学报, 2013, 35(4): 896-900.
Li Yan-bing, Du Lan, Liu Hong-wei, et al.. Study on classification of wheeled and tracked vehicles based on micro-Doppler effect and multilevel wavelet decomposition[J].Journal of Electronics & Information Technology, 2013, 35(4): 896-900.
[3] 韩勋, 杜兰, 刘宏伟, 等. 基于时频分布的空间锥体目标微动形式分类[J]. 系统工程与电子技术, 2013, 35(4): 684-691.
Han Xun, Du Lan, Liu Hong-wei, et al.. Classification of micro-motion form of space cone-shaped objects based on time-frequency distribution[J]. Systems Engineering and Electronics, 2013, 35(4): 684-691.
[4] 邵长宇, 杜兰, 李飞, 等. 基于多目标跟踪的空间锥体目标微多普勒频率提取方法[J]. 电子与信息学报, 2012, 34(12): 2972-2977.
Shao Chang-yu, Du Lan, Li Fei, et al.. Micro-doppler extraction from space cone target based on multiple target tracking[J]. Journal of Electronics & Information Technology, 2012, 34(12): 2972-2977.
[5] 罗迎, 柏又青, 张群, 等. 弹道目标平动补偿与微多普勒特征提取方法[J]. 电子与信息学报, 2012, 34(3): 602-608.
Luo Ying, Bai You-qing, Zhang Qun, et al.. Translational motion compensation and micro-Doppler feature extraction of ballistic targets[J]. Journal of Electronics & Information Technology, 2012, 34(3): 602-608.
[6] Luo Ying, Zhang Qun, Qiu Cheng-wei, et al.. Micro-Doppler effect analysis and feature extraction in ISAR imaging with stepped-frequency chirp signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2087-2098.
[7] 李飞, 纠博, 绍长宇, 等. 目标微动参数估计的曲线跟踪算法[J]. 电波科学学报, 2013, 28(2): 278-284.
Li Fei, Jiu Bo, Shao Chang-yu, et al.. Curve tracking based parameter estimation of micro-motion[J]. Chinese Journal of Radio Science, 2013, 28(2): 278-284.
[8] 黄小红, 贺夏, 辛玉林, 等. 基于时频特征的低分辨雷达微动多目标分辨方法[J]. 电子与信息学报, 2010, 32(10): 2342-2347.
Huang Xiao-hong, He Xia, Xin Yu-lin, et al.. Resolving multiple targets with Micro-motions based on time-frequency feature with low-resolution radar[J]. Journal of Electronics & Information Technology, 2010, 32(10): 2342-2347.
[9] 关永胜, 左群声, 刘宏伟. 高噪声环境下微动多目标分辨[J].电子与信息学报, 2010, 32(11): 2630-2634.
Guan Yong-sheng, Zuo Qun-sheng, and Liu Hong-wei. Micro-motion targets resolution in a high noise environment [J]. Journal of Electronics & Information Technology, 2010, 32(11): 2630-2634.
[10] 杨有春, 童宁宁, 冯存前, 等. 利用最强散射点信息的平动补偿与微多普勒提取[J]. 西安电子科技大学学报(自然科学版), 2012, 39(6): 147-153.
Yang You-chun, Tong Ning-ning, Feng Cun-qian, et al.. Translation compensation and micro-doppler extraction by using the information on the strongest scatter[J]. Journal of Xidian University, 2012, 39(6): 147-153.
[11] 魏少明, 王俊, 孙进平, 等. 弹道中段目标平动径向速度估计的状态空间法[J]. 电子与信息学报, 2013, 35(2): 413-418.
Wei Shao-ming, Wang Jun, Sun Jin-ping, et al.. A state space method for estimating the translational radial velocity of ballistic targets[J]. Journal of Electronics & Information Technology, 2013, 35(2): 413-418.
[12] Camp W W, Mayhan J T, and O’Donnell R M. Wideband radar for ballistic missile defense and range doppler imaging of satellites[J]. Lincoln Laboratory Journal, 2000, 12(2): 267-280.
[13] 朱丰, 张群, 梁必帅, 等. 频谱稀疏OFD-LFM弹头自旋微动特征重构方法[J]. 电子科技大学学报, 2013, 42(3): 369-374.
Zhu Feng, Zhang Qun, Liang Bi-shuai, et al.. Reconstruction method of spinning micro motion signature of missile with sparse frequency OFD-LFM signal[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(3): 369-374.
[14] Ma Liang, Liu Jin, Wang Tao, et al.. Micro-Doppler characteristics of sliding-type scattering center on rotationally symmetric target[J]. SCIENCE CHINA Information Sciences, 2011, 54(9): 1957-1967.
[15] 姚辉伟, 魏玺章, 徐少坤, 等. 弹道中段进动目标非理想散射中心微动特性研究[J]. 电子学报, 2012, 40(9): 1844-1851.
Yao Hui-wei, Wei Xi-zhang, Xu Shao-kun, et al.. Micro-motion characteristics of non-ideal scattering centers of midcourse targets with precession[J]. Acta Electronica Sinica, 2012, 40(9): 1844-1851.
[16] 陈广锋. 基于Radon变换的目标主体信号与微动信号的分离[J]. 科学技术与工程, 2013, 13(20): 5811-5814.
Chen Guang-feng. The separation of main body signal and micro-motion signal based on radon transformation[J]. Science Technology and Engineering, 2013, 13(20): 5811-5814.
胡晓伟: 男,1987年生,博士生,研究方向为雷达成像与识别.
童宁宁: 女,1963年生,教授,博士生导师,研究方向为综合电子战和多基地雷达信号处理.
董会旭: 男,1987年生,博士生,研究方向为雷达成像技术.
初洪帅: 男,1989年生,助理工程师,研究方向为雷达成像技术.
Translation Compensation and Resolution of Multi-ballistic Targets in Midcourse
Hu Xiao-wei①Tong Ning-ning①Dong Hui-xu①Chu Hong-shuai②
①(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)
②(Unit 95920 of PLA, Cangzhou 253801, China)
Time-frequency image of multi-ballistic targets is composed of micro-Doppler of multi-targets with multi-scattering centers, which makes the methods for single target invalid. Firstly, micro-Doppler of precessing missile and swinging decoy is analyzed. Considering midcourse ballistic targets’ characteristics that the motion is stable and the acceleration is approximately a constant in short time, Radon transform is applied to the detection of linear degree of the micro-Doppler, then motional parameters are estimated based on minimum entropy criteria and Gauss fitting. After compensating translation, Viterbi algorithm is used to extract micro-Doppler from the time-frequency image, with which multi-targets can be resolved according to the principle that scattering centers on one target are with the same micro-Doppler cycles, but those on different targets are not. Finally, Simulations verify the effectiveness of the proposed method.
Ballistic targets; Micro-Doppler; Translation compensation; Radon transform; Multi-targets resolution
TN957.51
A
1009-5896(2015)02-0291-06
10.11999/JEIT140494
2014-04-15收到,2014-07-21改回
国家自然科学基金(61372166)资助课题
*通信作者:胡晓伟 601237134@qq.com

