考虑弹性支撑的索力估算

徐霞飞，张平乐

考虑弹性支撑的索力估算

徐霞飞，张平乐

(湖南省武靖高速公路建设开发有限公司，湖南邵阳422400)

本文利用D’Alembert原理，对索在弹性支撑条件下的自由振动频率方程和索力的解析表达式进行了推导,并与有限元结果进行了比较．结果表明，利用振动法测索力时，考虑索弹性支撑条件，可运用本文给出的索力公式进行索力估算．

弹性支撑条件；频率；振动法；索力

目前，振动法是索力估算中采用最广泛的方法[1-3]．而现今几乎所有索力是假定索两端的边界约束为理想的固支或简支条件下采用梁理论或弦理论而求得[4-5]．但索的实际边界并不是理想的固支或简支，索力的估算精度会受实际边界条件的影响[6]．本文利用D’Alembert原理，推导出了索在弹性支撑下的自由振动频率方程和索力的解析表达式，并与有限元结果进行了比较．

1 索的基本方程及其求解

1.1索的基本方程

不考虑索本身的抗弯刚度影响，索的自由振动微分方程可以由D’Alembert原理推导得出[7]

式中T为索力；(,)u x t为索的横向位移函数；x为纵向坐标；()m x为索的单位长度的质量；t为时间．

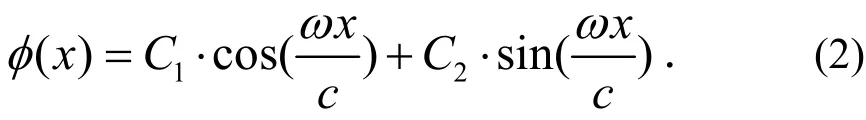
方程(1)为线性微分方程，索的振型函数可采用分离变量法求得式中w为索的自振频率；1C-4C为根据初始条件和边界条件可确定的待定系数．

1.2弹性支撑条件下的自由振动频率方程

结合索的实际边界约束条件，不考虑索的抗弯刚度的影响，运用弦理论，建立如图1的力学模型，其边界条件满足

式中1K¢、3K¢为索两端的竖向支承刚度．

图1 索在弹性支撑条件下的弦模型

引入两个无量纲参数1k¢、3k¢，其中

式中1k¢、3k¢在0-¥之间取值，取两端点值时，表示不同的特殊支撑刚度．

将式(2)、(4)代入式(3)得

因为1C、2C不可能同时为零，故式(5)的系数行列式的值一定等于零，即

展开式(6)化简得

式中

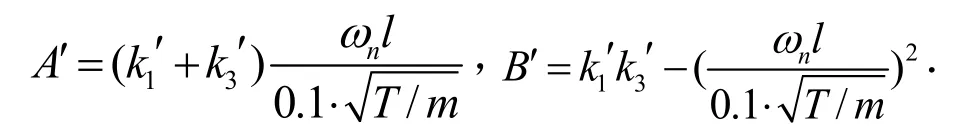
式(7)为索在弹性支撑条件下的自由振动特征频率方程，此特征方程为一无法直接求解的超越方程，但可以通过迭代的方法求解．

近一步将式(7)简化得

式中

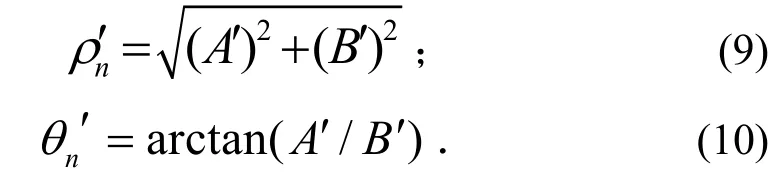
n表示所求索的频率的阶数．

由于A¢、B¢不可能同时等于零，则一定有

这样以下函数可以被定义：

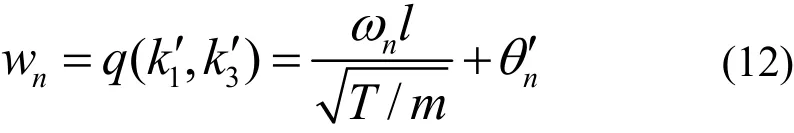
2.1特征频率方程的数值分析

首先假定不同的边界支撑条件，求解无量纲特征频率方程，将其结果代入上述(12)中，就可得到此函数的各阶函数值．

2 自由振动特征频率方程数值分析

(1)当0£k1¢£78.000 0且0£k3¢£78.000 0时，使无量纲参数k1¢、k3¢分别取下列几组不同值：k1¢=0、0£k3¢£78.000 0；k1¢=78.000 0、0£k3¢£78.000 0；0£k1¢=k3¢£78.000 0；则方程(12)的前三阶值的柱状图如图2所示．

图2 不同支撑刚度下函数nw前三阶值的柱状图

由图2可知：当0£k1¢£78.000 0且0£k3¢£78.000 0时，对于第一、第二阶频率，式(12)没有统一的函数值；但对于第三阶频率，w3的值都接近于2p．

(2)当78.000 0£k1¢且78.000 0£k3¢时，使无量纲参数k1¢、k3¢分别取下列几组不同值：k1¢=78.000 0、78.000 0£k3¢£1 000.000 0；k1¢=1 000.000 0、78.000 0£k3¢£1 000.000 0；78.000 0£k1¢=k3¢£1 000.000 0．则方程(12)的前三阶值的柱状图如图3所示．

图3 不同边界刚度下函数nw前三阶值的柱状图

由图3可知：当1k¢³78.000 0且3k¢³78.000 0时，对于第二、第三阶频率，式(12)没有统一的函数值；而对于第一阶频率，1w的值都接近似等于p．

综上所述：在讨论范围内，对于第一阶频率，函数1w的值都近似等于p，那么可假设得对于第三阶频率，函数3w的值都近似等于2p，那么可假设得

2.2特征频率方程的解

索在考虑边界约束条件影响时，由上述数值分析所得结论可知，其自振频率可按下式计算：

(1)当1k¢³78.000 0且3k¢³78.000 0时，对于第一阶频率，由

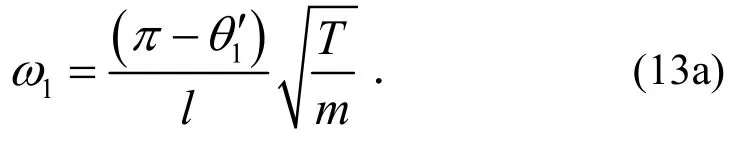
(2)当0£k1¢£78.000 0且0£k3¢£78.000 0时，对于第三阶频率，由可知

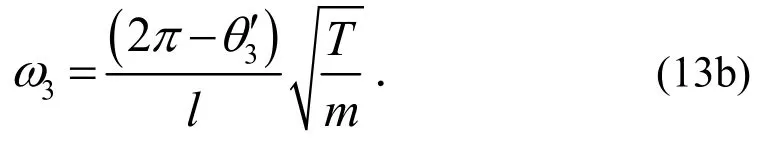
式中1w、3w分别表示索的第一、第三阶频率；其它符号同前．

式(13)为索的频率表达式，其解需要通过迭代才能求得．首先由已知的边界条件1K¢、3K¢和索力T的值，先假定一近似的初始频率1w或3w，然后代入式(10)求得1q¢或3q¢，再代入公式(13)求得1w或3w，如果前后两次频率之差小于容许误差，则迭代停止，否则，继续循环迭代，至之满足所需的精度为止．

3 弹性支撑条件下的索力公式

从式(13)可变形得索的索力估算公式(14)．l

采用第一阶频率进行索力估算时

(k1¢>78.000 0且k3¢>78.000 0)；

l采用第三阶频率进行索力估算时

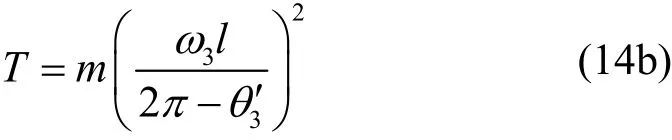
(01k¢££78.000 0且03k¢

££78.000 0)．式中1w、3w分别表示索的第一、第三阶实测频率；其它符号同前．

上述两式为采用索的第一阶和第三阶频率运用弦理论求得的考虑弹性支撑条件的索力估算的一般表达式．式(14)是迭代表达式，通过已知的边界条件1K¢、3K¢和实测频率1w或3w，先假定设计索力为索力的初值0T，然后代入式(10)求得1q¢或3q¢，再代入索力估算公式(14)求得索力T，如果前后两次索力之差小于容许误差，则迭代停止，否则，继续循环迭代，至之满足所需的精度为止．

本文给出的索力公式最关键的是正确测量出索的第一阶或第三阶频率，关于索的频率的测试可参见文献[8-9]．

4 索力公式验证

现任取一根索，其索的物理参数见表1所示．

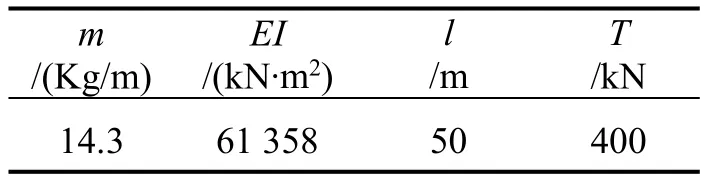
表1 索的物理参数

考虑此索受不同弹性支撑条件的约束，通过有限元计算出此索在相应弹性支撑条件下的各阶频率，将本文公式(14)与真实索力计算结果比较见表2．

表2 索力计算值的比较(kN)

表中1K¢、3K¢、为支撑刚度，偏差为本文公式与真实索力之差的偏差，由上表可知，采用本文公式计算索在弹性支撑条件下的索力具有足够的精度．

4 结论

本文利用D’Alembert原理，对索在弹性支撑条件下的自由振动频率方程和索力的解析表达式进行了推导,并与有限元结果进行了比较．结果表明，考虑索的弹性支撑条件时，可运用本文索力公式进行索力估算．

[1]Russell J C,Lardner TJ.Experimental determination of frequenciesandtensionforelasticcables[J].Journalof Engineering Mechanics,ASCE,1998,124(10):1067-1072.

[2]Kroneberger Stanton K J,Hartsough B R.A monitor for indirect measurementofcablevibrationfrequencyandtension[J]. Transaction of theASCE,1992,35(3):341-346.

[3]Casas J R.A combined method for measuring cable forces:the Cable Stayed Alamillo Bridge,Spain[J].Structural Engineering International,1994,4(3):235-240.

[4]董建华.中、下承式拱桥吊索的模态分析与张力测定[D].郑州大学硕士学位论文,2004.

[5]Zui H,Shinke T,Namita Y.Practical formulas for estimation of cable tension by vibration method[J].Journal of Structural Engineering,ASCE,1996,122(6):651-656.

[6]方志,张智勇.斜拉桥的索力测试[J].中国公路学报,1997, 10(1):51-58.

[7]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社, 2003.

[8]陈刚,任伟新.基于环境振动的斜拉桥拉索基频识别[J].地震工程与工程振动,2003,23(3):100-106.

[9]陈刚.振动法测索力与实用公式[D].福州大学硕士学位论文, 2004.

(责任编校：陈智全)

Estimation of Cable Tension under Elastic Support Conditions

XU Xia-fei,ZHANG Ping-lei
(Hunan Wu Jing Highway Construction and Development Co.,Ltd.,Shaoyang,Hunan 422400,China)

In this paper,according to D’Alembert principle,the natural frequency equation and the explicit expression of the cable tension with elastic support conditions are deduced,and compared with finite element results.The results show that the tension of cable measurement by vibration method considering the elastic support conditions of cable,the formula to cable tension is given in this paperand it can be used to calculate the tension of cable.

elastic support conditions;frequency;the vibration method;cable tension

U443.38

A

10.3969/j.issn.1672-7304.2015.01.005

1672–7304(2015)01–0019–04

2014-12-13

徐霞飞(1979-)，男，湖南汉寿人，硕士研究生。主要从事索结构研究、桥梁隧道施工管理．