平面轨迹机构的静态综合可靠性分析

李 奇, 张均富

(西华大学机械工程学院，四川 成都 610039)

·机电工程·

平面轨迹机构的静态综合可靠性分析

李 奇, 张均富*

(西华大学机械工程学院，四川 成都 610039)

传统的机构运动可靠性研究多以各分量运动误差来建立机构运动的可靠性分析模型，进而获得各分量误差落在允许误差范围内的概率。为获得各分量误差的综合效应，将机构运动在每一坐标分量上的失效看作一种失效模式，基于多失效模式提出轨迹机构的综合运动可靠性分析模型。在各运动分量的相关性分析的基础上，采用二维正态分布导出各运动分量的联合概率密度，最后采用数值积分方法求解机构运动综合可靠度。通过数值实例对该模型的有效性和精度进行验证，其结果表明，这一模型能够反映机构在整个运动区间上某指定点处整体失效情况。

运动可靠度;轨迹机构;多失效模式

轨迹再现机构的设计是机构综合问题的重要内容。近年来，学者们特别关注轨迹机构的综合模型的建立和其算法的求解[1]， 旨在提高机构的运动精度。在确定性条件下，现有机构综合模型及其求解方法是十分有效的，但在真实机构系统中不确定性是固存的，如尺寸公差、运动副间隙、构件材料与弹性变形等。这些不确定性使机构的真实运动偏离期望运动轨迹，造成机构的运动精度降低、可靠性下降。为提高轨迹生成的精度，应综合考虑不确定性因素对机构运动的影响。

机构系统中存在的不确定性常看作随机不确定性。机构运动可靠性理论就是应用概率统计理论研究这些随机不确定性问题的方法和理论。轨迹机构的运动可靠性问题已被广泛的研究[2-8]，现有方法多数是基于机构输出点的各运动分量误差(欧氏误差)模型提出机构的运动可靠性分析模型。该模型分别求解机构在各运动分量上再现期望轨迹的概率，难以体现机构在运动区间上某指定点处机构的整体失效情况，即机构在该点的综合可靠度。Zhang等[5]将这种综合可靠度定义为轨迹机构的系统可靠度，但没考虑各分量之间的相关性。Huang等[6]采用结构工程领域的系统可靠度分析的矩阵法对轨迹机构系统可靠度的求解进行研究，但得到的可靠度是机构运动可靠度的上下限。在现有文献中，机构运动可靠度分为点可靠度和时变可靠度[7]。点可靠度研究机构在某时间点处的运动误差落在许用误差范围内的概率，而时变可靠度研究机构在整个指定运动区间上的运动误差不超过许用误差的概率。前者为静态可靠度，后者为动态可靠度[9]。本文将轨迹机构输出点的每个分量误差超出允许误差限看作一种失效模式，以多失效模式建立轨迹型机构的可靠性分析模型，并应用该模型研究求解机构在指定时间点处的静态综合可靠度问题。

1 机构运动可靠性模型

图1为一平面四杆轨迹机构，构件AB为机构的输入曲柄，θ为曲柄AB相对机架AD的转角。连杆BC与构件BP固连且夹角为β。φ为机架AD与坐标系x轴的夹角。L1、L2、L3、L4、L5分别为机架AD、曲柄AB、连杆BC、摇杆CD、构件BP的杆件长度。

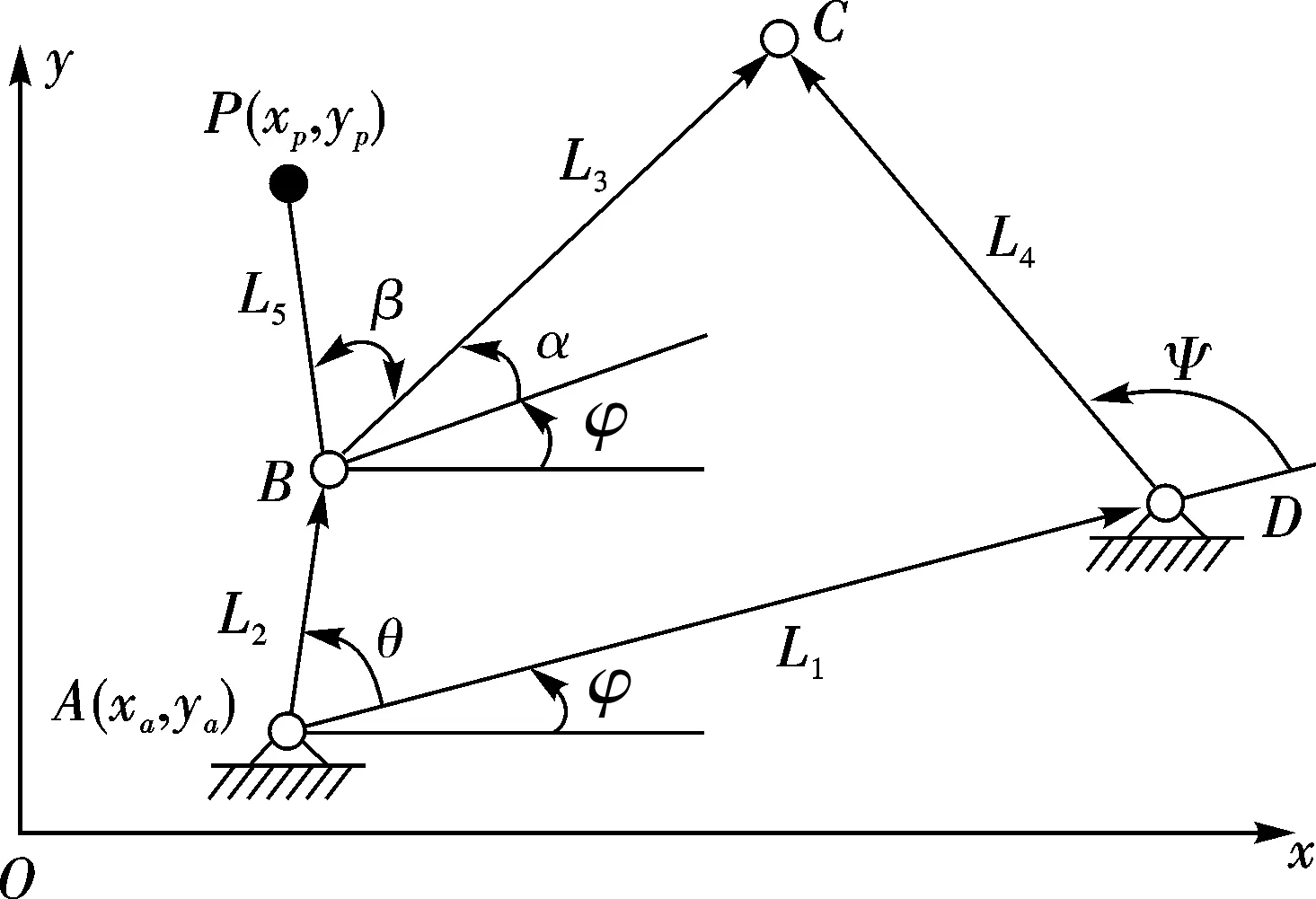
图1 平面四杆轨迹机构

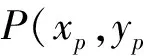
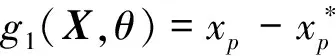
(1)

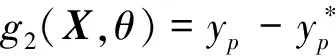
(2)

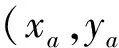
考虑机构系统中的随机性，即各尺寸参数的制造公差和机构的安装误差，则X为随机向量。传统研究按各误差分量形式定义机构的运动可靠性模型，即:

1)在x方向，机构在曲柄转角θ处的可靠度R1(θ)为

(3)

2)在y方向，机构在曲柄转角θ处的可靠度R2(θ)为

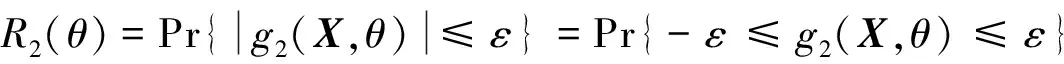
(4)

式中，ε为机构的运动误差限。

上述可靠性模型仅能反映机构运动误差分量落在允许误差范围内的概率。在机构的不确定性(概率)综合时，人们更多地关注机构在曲柄转角θ处各误差的综合效应，即机构的运动误差分量同时落在允许误差范围内的概率。为此，可将各运动分量的失效看作一种失效模式，基于多失效模式定义机构运动可靠性模型，为

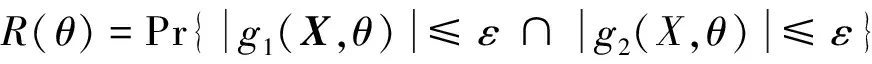
(5)

式(5)中，由于同时考虑了机构运动在坐标x、y方向上的误差，因此称其为机构在曲柄转角θ处的综合可靠度。

2 机构运动可靠性分析

2.1各分量可靠性分析

假定各随机变量服从正态分布，即X～N(μX,σX)，且假定σX相对于μX非常小，则式(3)(4)定义的运动可靠度可由一次二阶矩方法(FOSM)高精度求解，即

(6)

对应的机构运动精度失效概率为

pfi(θ)=1-Ri(θ)。

(7)

式中，μi(X,θ)、σi(X,θ)(i=1,2)分别表示机构运动误差函数gi(X,θ)的均值和均方差。

根据FOSM 方法，μi(X,θ)、σi(X,θ)可由运动误差函数gi(X,θ)在X的均值处线性展开获得,用泰勒公式线性化gi(X,θ)可得

(8)

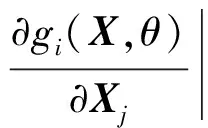
作变换Xj=μXj+σXj·Uj，其中Ui～N(0,1)，于是，式(8)可改写为

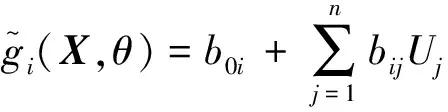
(9)

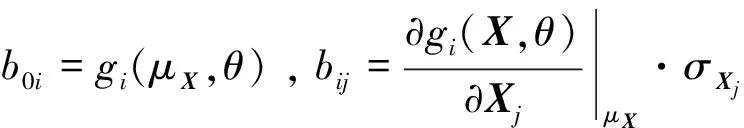
μi(X,θ)=b0i；

(10)

σi(X,θ)=‖bi‖。

(11)

式中bi=[bi1,bi2,…,bin]。

2.2综合可靠性分析

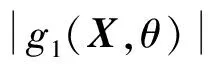
σ12(X,θ)=E[(g1(X,θ)-μg1(X,θ))(g2(X,

θ)-μg2(X,θ))]。

(12)

将式(9)带入式(12)得到

σ12(X,θ)=b1·b2。

(13)

式中，b1=[b11,b12,…,b1n]，b2=[b21,b22,…,b2n]。

由此写出g1(X,θ)与g2(X,θ)的相关系数

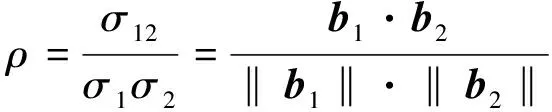
(14)

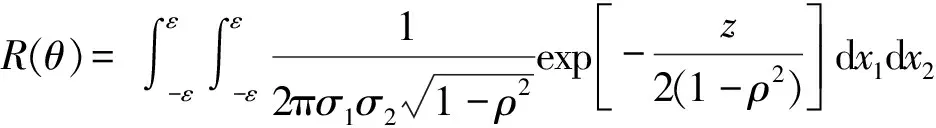
(15)

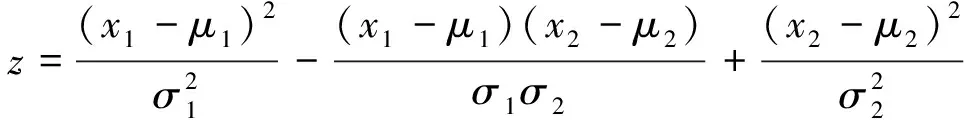
3 实例分析

以图1所示平面四杆机构为例再现期望轨迹，如表1所示。为简化，将机架杆1的方位角φ、输出杆5与连杆3的夹角β、铰链点A的坐标处理为确定性参数，机构杆长尺寸作为随机变量，即X=(L1,…,L5)。各尺寸变量均服从正态分布，其均指为μX=(79.516 1,9.724 0,45.842 5,51.432 8，8.728 9)，变异系数C=0.01，确定性变量φ=5.596 9 rad，β=-0.345 2 rad，铰链A的坐标(xa,ya)=(2.021 1,13.216 6)。机构运动输出允许的误差限ε=0.07。

由图1知，机构输出点P的轨迹坐标为：

(16)

连杆3的转角α可由机构环路方程式求解。机构环路方程式为：

(17)

根据式(17)，连杆转角α为

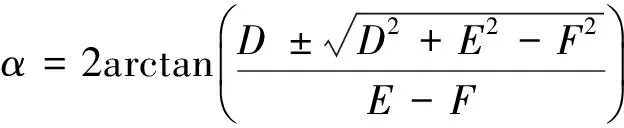
(18)

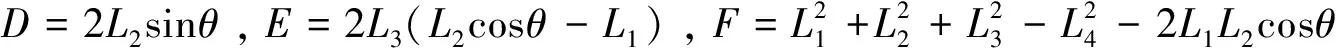
机构运动可靠度的求解流程如下。

1)根据式(16)～(18)对机构进行运动学分析，获得机构的实际输出轨迹。

2)根据式(16)和(17)，应用直接线性化方法可以得到误差传递系数bi(i=1,2)，进而获得gi(X,θ)的均值、均方差，以及g1(X,θ)与g2(X,θ)的相关系数。

3)根据式(6)和(7)求解机构各运动输出分量的可靠度或失效概率。

4)根据式(15)求解曲柄转角θ处的机构运动综合可靠度。

结合上述流程与方法，对实例进行分析得到机构的运动可靠度，如表2所示。为验证前述方法的精度，将蒙特卡洛方法(MCS)的计算结果作为精确值(其仿真次数为108)与本文方法进行比较。可以看出，各分量失效概率和综合失效概率与蒙特卡洛结果非常接近，由此验证了前述近似计算方法的有效性和精确性。

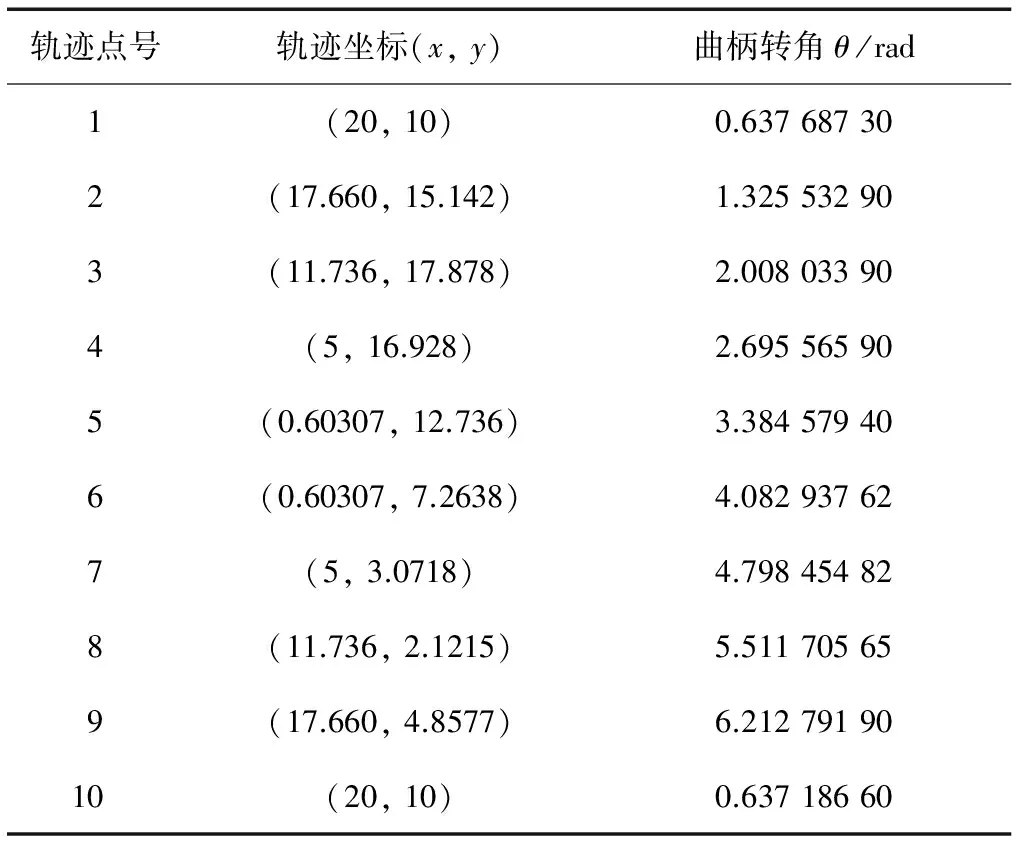
表1 机构期望再现轨迹

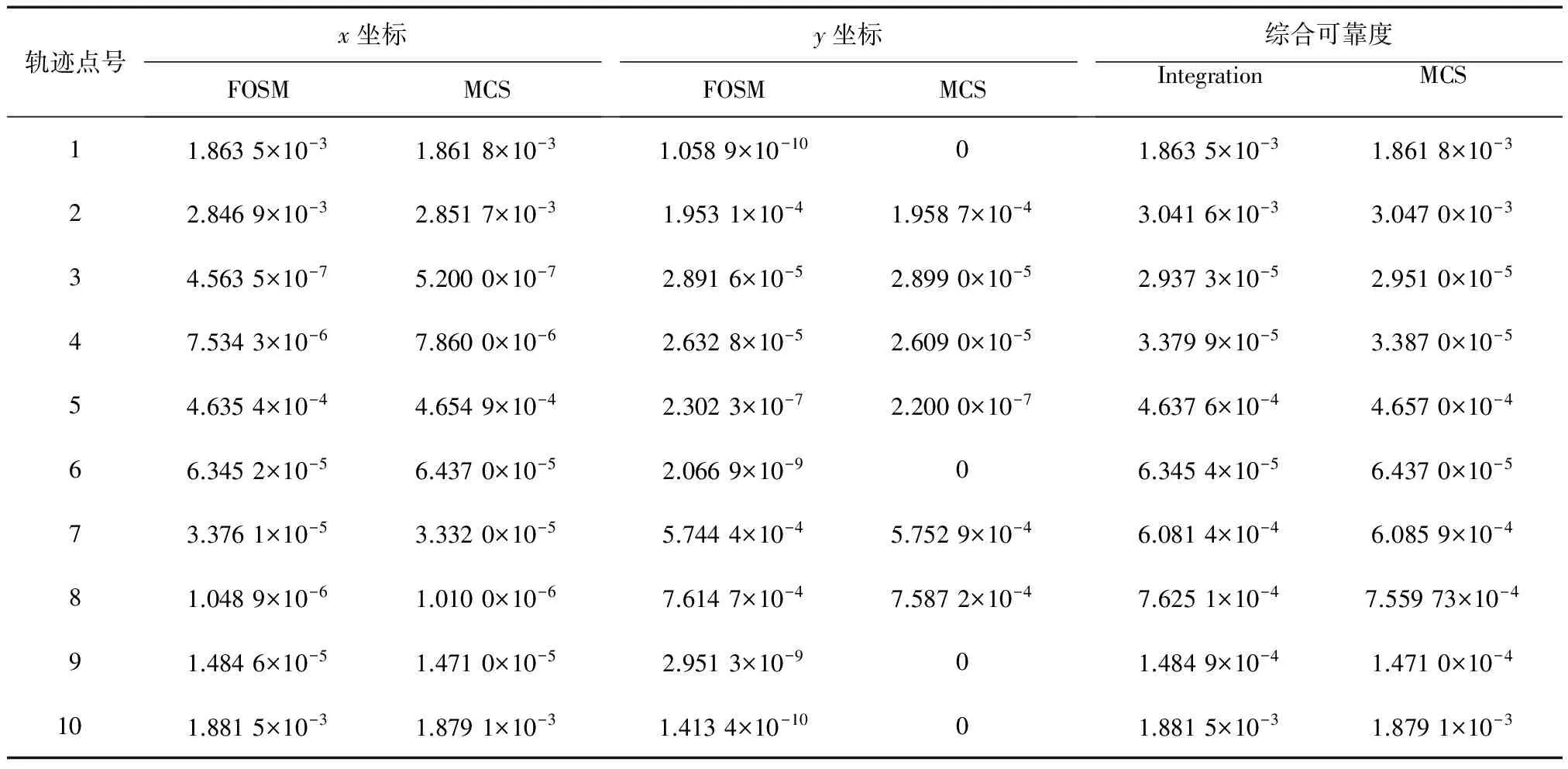
表2 机构的运动可靠度

4 结论

现有平面轨迹机构的不确定性研究多以机构各坐标分量上的运动误差为基础建立各运动分量可靠性分析模型。该模型不能很好地反映机构的整体运动失效情况。本文将机构在每一坐标分量上的运动看作一种失效模式，基于多失效模式提出轨迹机构的综合运动可靠性分析模型。在各运动分量的相关性分析基础上，采用二维正态分布导出了各运动分量的联合概率密度，最后采用数值积分方法求解机构运动综合可靠度。数值实例分析结果表明，本文所提出的基于各分量联合概率密度的数值积分法的求解结果非常接近蒙特卡洛方法的结果，而且该方法具有较高求解精度和较小的计算代价(与蒙特卡洛方法相比，在每个时间点上本方法仅调用1次机构分析程序，而蒙特卡洛方法调用108次)。此外，所提出的可靠性分析模型能够反映机构在整个运动区间上某指定点处整体失效情况，或者说反映了机构在某指定点能够再现期望轨迹的整体概率和能力。本文提出的可靠性分析模型及求解算法适用于轨迹机构运动可靠性分析，能全面、直观地反映机构的整体运动状况和再现轨迹的精度。

[1]Sanjay B Matekar, Gunesh R Gogate. Optimum Synthesis of Path Generating Four-bar Mechanisms using Differential Evolution and a Modified Error Function[J]. Mechanism and Machine Theory, 2012, 52(6):158-179.

[2]Liu T S, Wang J D. A Reliability Approach to Evaluating Robot Accuracy Performance[J].Mechanism and Machine Theory, 1994, 29(1): 83-94.

[3]Shi Z X. Synthesis of Mechanical Error in Spatial Linkages Based on Reliability Concept[J].Mech Mach Theory, 1997, 32(2): 255-259.

[4]Bhatti P K , Rao S S . Reliability Analysis of Robot Manipulators[J].Journal of Mechanisms, Transmissions, and Automation in Design, 1998, 110:175-181.

[5]Zhang Y, Huang X, Zhang X, et al. System Reliability Analysis for Kinematic Performance of Planar Mechanisms[J].Chinese Science Bulletin, 2009, 54(14): 2464-2469.

[6]Huang Xianzhen, Zhang Yimin. Probabilistic Approach to System Reliability of Mechanism with Correlated Failure Models[J].Mathematical Problems in Engineering，2012, ID 465853, 11 pages.

[7]张均富,龙进.不确定性下平面四杆转向机构的运动精度分析[J].西华大学学报:自然科学版,2011,30(3):17-20.

[8]张均富,梁丽,宋玉忠，等.平行直动推杆传动强度可靠性设计[J].西华大学学报:自然科学版,2005,24(3):58-59.

[9]Zhang J,Du X. Time-dependent Reliability Analysis for Function Generator Mechanisms[J].Journal of Mechanical Design, 2010, 133 (3): 031005- 031014.

(编校：饶莉)

StaticCompositeReliabilityofPlanarPathMechanisms

LI Qi, ZHANG Jun-fu*

(SchoolofMechanicalEngineering,XihuaUniversity,Chengdu610039China)

In traditional probabilistic mechanism analysis, reliability analysis model of path generating mechanisms is set up with motion error of each coordinate.Because these kinds of mechanisms have multiple motion output components. The probability that a mechanism realizes its desired motion within a specified error is then calculated. In this work, each component of motion is taken as a failure mode and the kinematic reliability analysis model of path generating mechanisms is proposed with multiple failure modes in order to obtain the comprehensive effect of component errors. Based on statistical correlation analysis of failure events, the joint probability density function of each motion error is obtained by using two-dimensional normal distribution. The kinematic reliability is then calculated with the numerical integration method. The method is demonstrated by the analysis of a four-bar path generating mechanism.This model can provide a global failure of probability at a specified point during the motion interval.

kinematic reliability; path mechanisms; multiple failure modes

2014-06-24

国家自然科学基金资助项目(51275425)；教育部“春晖计划”资助项目(z2011081)。

：张均富(1972—)，男，教授，博士，主要研究方向为机构概率设计、机器人机构学。

TH112;TH115

：A

：1673-159X(2015)03-0017-04

10.3969/j.issn.1673-159X.2015.03.004

*