简单图的子图及其性质研究

周丽霞

(无锡城市职业技术学院 会计系，江苏 无锡 214000)

简单图的子图及其性质研究

周丽霞

(无锡城市职业技术学院 会计系，江苏 无锡 214000)

给出图论中关于子图的定义,并得到子图的一些性质。通过定理阐述子图与其导出子图的同构性、子图与哈密尔顿图的关系,并证明和举例。

图论;子图;同构;哈密尔顿图

本文给出了子图的定义,并研究了子图的一些性质和它与其导出子图的一些关系。本文所引用的定义及符号详见文献[1],文章所涉及的图均为无端点图。

在图论中,自环是两端连接着同一端点的边。既不含平行边又不含自环的图称为简单图[1]。给定1个简单图

G=(V,E),我们可以定义它的子图H,即取G的边集E作为H的顶点集,对H的边集W作如下规定:若G中任一点v在G中只关联边x,y,则令无序对(x,y)∈W,若v在G中关联边x1，…，xn(n>2,n为正整数),则在x1,…,xn中任选出2条边xi,xj,令无序对(xi,xj)∈W。若V′是V的1个非空子集,以V′为顶点集,以两端点均在V′中的边的全体为边集所组成的子图,称为G的由V′导出的子图,简称为G的导出子图[2]。

依定义可知,G的顶点集和边集与H的边集和顶点集是一一对应的。

1 子图的性质

由子图H的定义可知,图G的子图H不唯一(见图1)且有以下性质。

定理1图G=(V,E)的子图(指标号图)H的个数为

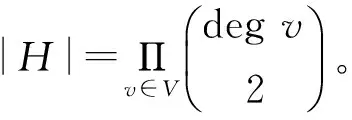
(1)

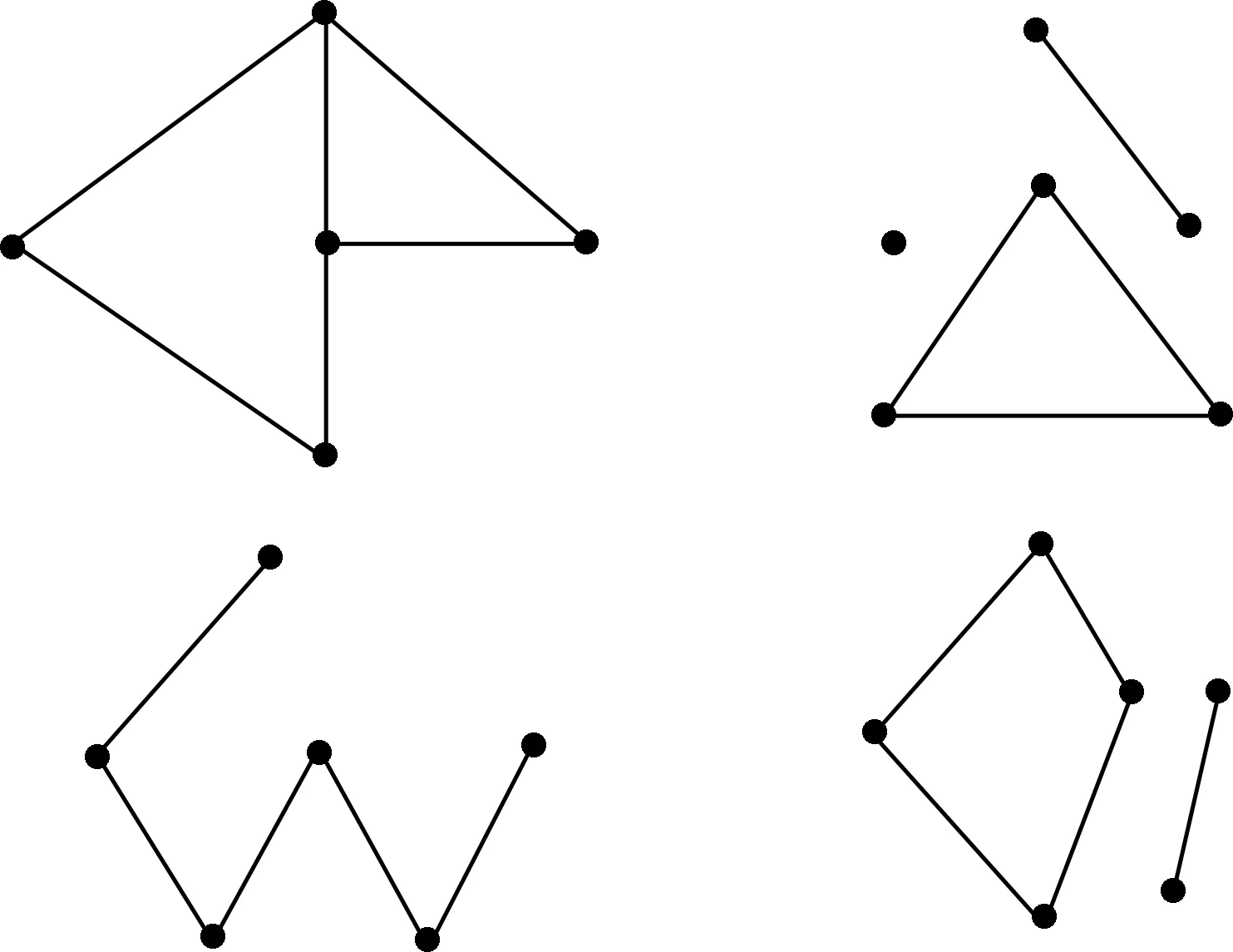
图1 图G及其3个子图

设G=(V，E)是没有孤立点的图，其边数为m，由于每条边都有两种选择，即包含于或不包含于某个子图，如果子图每条边都包含就是图G，如果每条边都不包含，就是空图，故必有简单图G中所有不同的生成子图(包括G和空图)的个数是2m。

事实上,当图包含某边时,也就意味着包含了与该边关联的2个顶点,故不同的子集个数为

一个图是子图,它要满足什么样的条件呢?

定理2一个图Q=(U,W)是子图当且仅当它满足:

1) degu≤2,∀u∈U;

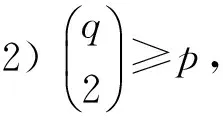
若一条途径有正的长且起点和终点相同,则称之为途径为闭的,闭途径也称为回路。若一条闭迹的起点和内部顶点互不相同,则称之为圈。下面利用圈的概念和性质来证明定理2。

证明必要性。若Q是子图,由定义可知,在子图中相关联的顶点、边在其导出子图中对应的边、顶点也相关联。对∀u∈U,若u关联3条或3条以上的边,则u在其导出子图中对应的边就要关联3个或3个以上的顶点，矛盾,故u最多关联2条边，即

degu≤2,

∀u∈U,

又因为Q的顶点数与边数对应其导出子图的边数和顶点数,故有

其中

p=|U|,

q=|W|。

充分性。若Q满足条件1),则它的每一个分支只可能是1个圈、1条道路或者孤立点。现构造如下图:考察Q的线图[3]L,它由一些圈、道路、孤立点组成。令L中的端点与它中间1个与此端点无线连的点联线,令L中的孤立点与它中间的2个与此孤立点无线连的点联线,由条件2)可知，此联法是可行的。这样,我们得到1个图G′(见图2)。

图2 子图及其构造图

对于Q中每一个孤立点,在G′中找出一对不相邻的点,在它们中间加1条线,并令这条线与这个孤立点对应,由条件2)可知,这种做法是可行的。如此得到1个图G。

从上面的构造步骤中,我们不难从它的对应关系中反过来构造1个与Q同构的G的子图,故Q是子图。

由此,我们证明了定理2的充要性,并用图2进行了直观的验证,1个图Q=(U,W)是子图所必备的条件。

2 子图与其导出子图的同构性

两个无向单纯图G1=(V1，E1)，G2=(V2，E2)，若这两个图的顶点间有一一对应关系，且在这种对应关系下保持“相邻”的关系不变，则这两个图称为是同构的，两个图同构时，将相对应的点取相同的顺序，则这两个图的相邻矩阵实际上是一样的。同构的图研究的是顶点之间的联系，在图论中是一样的图。

上面给出了子图和其导出子图的定义,根据图的同构[4]的定义得到定理3。

定理31个图G与它的1个子图同构当且仅当它是一些圈的并。

证明充分性。由于连通图同构于它的线图当且仅当它是1个圈,于是对于1个(不必连通的)图要同构,G是2度正则的。由此可见,1个图G与它的1个子图同构,则它是一些圈的并。

必要性。若图G与它的1个子图同构,图G中所有的点的度≥2,而它的子图中所有点的度≤2,故必然是一些圈的并。

证毕。

下面通过反例说明两个图在它们的所有不同构的子图中存在一一对应的关系,且对应的子图是同构的,它们本身并不一定同构。图3中两个图G1,G2的所有的子图(见图4)的集合是相同的，但它们本身并不同构。

通过反例,我们可以验证图和子图同构的前提条件。

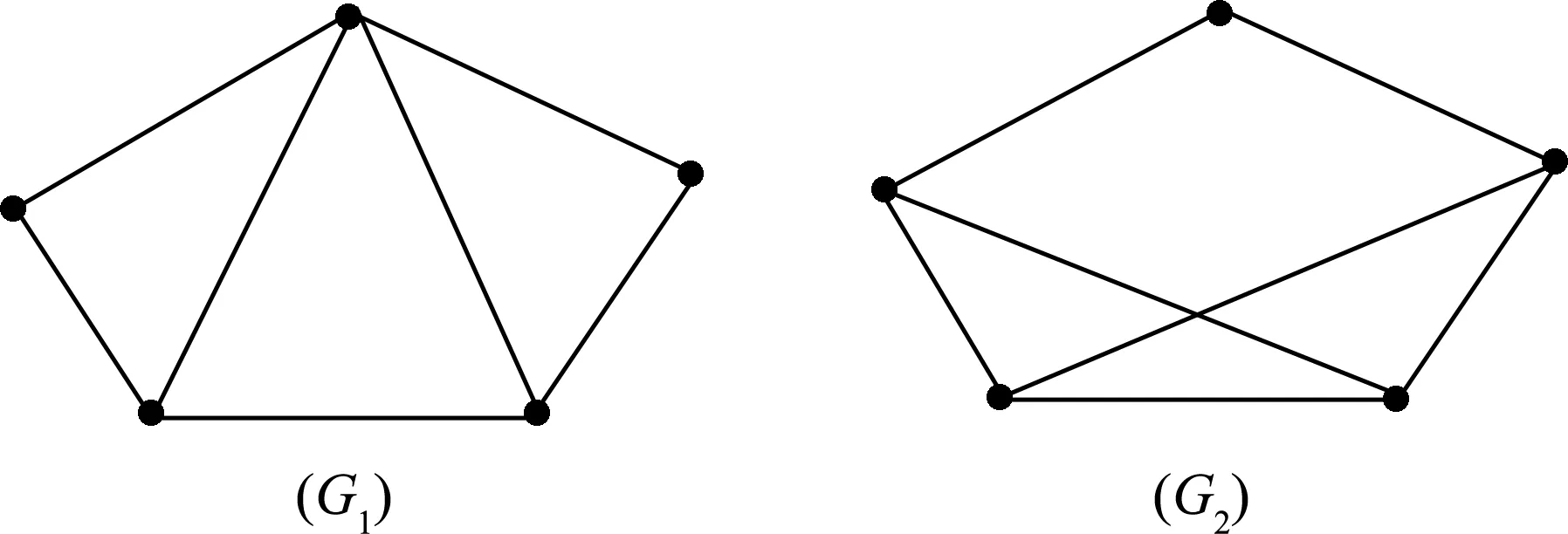
图3 不同构的图

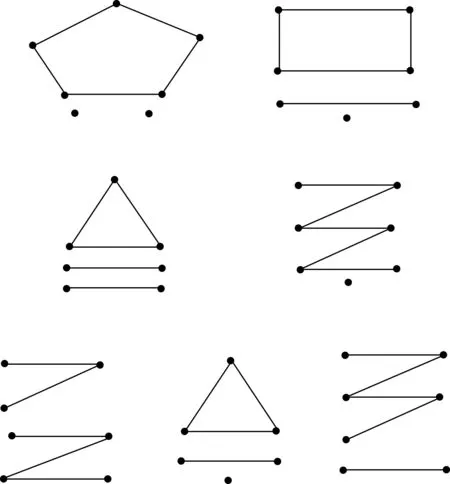
图4 G1,G2的子图集

3 子图与哈密尔顿图的关系

经过图G中每个点仅有一次路(圈)称为G的哈密尔顿路(圈)，存在哈密尔顿圈的图称为哈密尔顿图，简称H图，哈密尔顿路也简称为H路。下面就子图和哈密尔顿图的关系给出引理，进而得出定理4。

引理对每个子图的每个圈[5],它的导出子图G-v中必有1个长度相等的圈与之对应。

证明由定义可知，在H中相应的边邻接,则在G中对应的顶点也邻接。故对H中圈上的每条边,G中有1个顶点与之对应,边邻接对应顶点邻接,则G中有1个长度相等的圈与它对应。

对于连通图G,若G中存在经过每条边的闭迹(即Euler闭迹),则称G为Euler图。

定理41个图G是哈密尔顿图当且仅当它的子图集{H}中有1个是欧拉图。

证明充分性。若{H}中有1个是欧拉图,则只有含所有边的单圈情形,由引理1可知,G中有1个长度相等的圈与之对应,而子图的边集和其导出子图的点集是一一对应的。故此圈含G中所有的顶点,则G是哈密尔顿图。

必要性。若G是哈密尔顿图,则它至少含有1个哈密尔顿圈[6]。我们来构造1个图P′,令G中哈密尔顿圈上的顶点集和边集交换仍得到1个圈,令此圈上的所有边组成P′的边集,对G中除哈密尔顿圈上的边外的每一条线,令P′中1个孤立点与之对应,这些孤立点加上新构成的圈上的那些顶点组成P′的顶点集,则P′是G的1个子图且为欧拉图。

证毕。

与欧拉图的情形相反，到目前为止，哈密尔顿图仍然有很多尚未解决的问题，包括哈密尔顿图的非平凡充要条件问题。关于H图的研究仍是当前图论中比较活跃的领域。希望将来，通过算法和编程的应用更好更快地解决图论中的若干难题。

[1] 李慰萱.图论[M].长沙:湖南科学技术出版社,1980:9-24.

[2] 哈拉里F.图论[M].李慰萱,译.上海:上海科学技术出版社,2008:75-98.

[3] 张先迪,李正良.图论及其应用[M].北京:高等教育出版社,2005:1-20.

[4] 李修睦.图论导引[M].武汉:华中工学院出版社,1982:203-244.

[5] 宁万涛.图中的度、边和圈[D].兰州：兰州大学,2011:15-34.

[6] 张建高.一类路图的哈密尔顿圈[J].重庆建筑工程学院学报,1991(3):1-6.

〔责任编辑：卢 蕊〕

Researchonsubgraphofsimplegraphanditsproperties

ZHOU Li-xia

(Accounting Department,Wuxi City College of Vocational Technology,Wuxi 214000,China)

This paper gives the definition of subgraph in graph theory,and obtains some properties of subgraph. This paper expounds the subgraph amd the isomorphism induced by the subgraph,and the relationship between subgraph and Hamilton graph. The proof and examples are shown.

graph theory; subgraph; isomorphism; Hamiltonian graph

2015-03-11

周丽霞(1976—),女,江苏常熟人,讲师,硕士,主要从事高职数学教学和统计研究。

O158

：C

：1008-8148(2015)03-0066-03