速度拖引干扰和杂波背景下脉冲多普勒雷达目标跟踪算法

李迎春王国宏 关成斌 孙殿星

(海军航空工程学院信息融合研究所 烟台 264001)

速度拖引干扰和杂波背景下脉冲多普勒雷达目标跟踪算法

李迎春*王国宏 关成斌 孙殿星

(海军航空工程学院信息融合研究所 烟台 264001)

针对在速度拖引干扰和杂波背景下脉冲多普勒(PD)雷达无法精确跟踪目标的问题，该文提出基于双模型(DM)和幅度信息(AI)的目标跟踪算法。分别建立基于位置、幅度量测的跟踪模型和基于位置、速度、幅度量测的跟踪模型。两个模型均使用基于幅度信息的概率数据互联(AI-PDA)尽可能地降低杂波的影响，然后使用常规方法进行滤波估计。若没有速度拖引干扰，则两个模型估计具有位置和速度上的相关性；若存在干扰，由于速度量测是虚假的，则两个模型估计不具有相关性。据此，进行卡方检验(chi-square test)，分析影响检验结果的因素，进而确定最终的估计结果。仿真验证了该算法的有效性。

雷达；目标跟踪；速度拖引干扰；双模型；幅度信息；卡方检验

1 引言

具备测速功能的脉冲多普勒(Pulse Doppler, PD)雷达因具有较强的杂波抑制能力和较高的跟踪精度而广泛应用于目标探测与跟踪[1]。为了削弱PD雷达的优势，目标往往实施速度欺骗干扰，通过发射速度欺骗信号，使PD雷达无法获得目标的真实速度量测[2]。速度拖引干扰是速度欺骗干扰的一种样式，其干扰信号的多普勒频移相对于真实目标的多普勒频移逐渐减小或增大，而功率却大于真实目标的回波信号功率，使雷达频率跟踪环路自动跟踪虚假的多普勒频率[3]。由于雷达载体具有运动速度，具有扩展多普勒频率谱的杂波会进入数据处理单元，且欺骗干扰常常伴随着噪声干扰或箔条干扰等，雷达无法有效抑制大量杂波。有规律变化的虚假速度量测和较多杂波造成雷达无法精确跟踪目标，跟踪航迹逐渐偏离目标航迹，最终目标跟踪丢失。

针对速度拖引干扰采取的有效反电子对抗措施(Electronic Counter-CounterMeasures, ECCM)主要基于雷达信号处理技术和雷达数据处理技术。基于雷达信号处理技术的ECCM主要有脉冲分集[4,5]、干扰信号相位量化差异[6,7]、自适应线性预测滤波[8]、干扰信号谐波分量调频率匹配检测[9]和多域联合处理[10]等。然而，高速发展的数字射频存储(DigitalRadio Frequency Memory, DRFM)等技术使虚假信号与雷达发射信号相干，使两种信号在波形、频率和相位调制方式、电磁散射特性等方面相差无几[11−13]，先进信号处理技术不可能完全剔除逼真度很高的虚假信息，虚假信息不可避免地进入雷达数据处理单元。基于雷达数据处理技术的ECCM主要是基于虚假速度量测信息与跟踪航迹的估计速度不匹配的原则，通过比较两个速度值的不同而鉴别出干扰[14,15]，即速度比较法。对于无杂波和目标匀速运动的情况，这种ECCM是有效的。然而，为了摆脱雷达跟踪，目标会做不同程度的机动，其速度是不断变化的，并且速度拖引干扰下的虚假速度量测进行有规律地递增或递减，造成跟踪航迹的估计速度随虚假速度量测发生变化。因此，用速度比较方法对抗目标机动和杂波条件下的速度拖引干扰的效果并不是很明显。

根据以上分析，针对速度拖引干扰和杂波背景下PD雷达目标跟踪问题，本文提出了基于双模型(Double Models, DM)和幅度信息(Amplitude Information, AI)的目标跟踪算法。算法建立了基于不同量测集的跟踪模型，两个模型均使用基于AI的概率数据互联(Probabilistic Data Association, PDA)进行数据关联，降低杂波的影响，然后利用匀加速(Constant Acceleration, CA)目标动态模型和基于量测转换的卡尔曼滤波(Converted Measurement Kalman Filtering, CMKF)算法进行滤波估计，分别得到不同的目标状态估计，对两个估计结果进行卡方检验和模型滤波发散程度比较，选择最终的目标状态估计。经仿真验证，在速度拖引干扰和杂波背景下该算法能稳定跟踪目标，航迹丢失率较低。

2 基于DM-AI的目标跟踪算法

2.1 双模型的建立

对于普通雷达，用于目标跟踪的量测数据主要是空间位置量测，而对于PD雷达，可用的量测数据不仅有目标空间位置量测，还有目标径向速度量测。若没有速度拖引干扰，雷达可以单纯利用空间位置量测进行目标跟踪，也可以利用空间位置加径向速度量测实现精度更高的目标跟踪；若存在速度拖引干扰，在有杂波和目标机动的情况下，雷达无法及时识别出干扰，仍会将虚假的径向速度量测用于目标跟踪，径向速度量测使跟踪滤波结果偏离目标真实状态。但是，速度拖引干扰只是产生了虚假的速度信息，雷达获得的目标空间位置量测仍是真实的，雷达利用空间位置量测仍能跟踪目标。

为此，依据不同的量测集合分别建立两个跟踪模型：基于空间位置、幅度量测的跟踪模型M1和基于空间位置、幅度、径向速度量测的跟踪模型M2。双模型结构如图1所示。

图1 双模型结构图

模型M1和M2各自独立地进行数据关联和循环滤波，分别获得目标状态估计向量1(k|k)和2(k|k)及相应的估计误差协方差P1(k|k)和P2(k|k)。若雷达没有受到速度拖引干扰，则1(k|k)和2(k|k)都是对目标状态的正确估计，两者具有相关性，其中由于径向速度量测参与滤波，2(k|k)的估计精度更高；若雷达受到速度拖引干扰，径向速度量测是虚假的，2(k|k)偏离了目标真实状态，则1(k|k)和2(k|k)不具有相关性。根据以上原则可制定模型选择规则，确定最后的目标状态输出。

2.2 数据关联和滤波估计

PD雷达具有抑制固定杂波的能力，然而在复杂环境下，源于自然环境的运动杂波会不可避免地进入雷达数据处理单元，而且干扰方在实施欺骗干扰的同时往往进行噪声干扰或箔条干扰，雷达载机和干扰机、箔条具有相对运动，导致干扰产生的杂波多普勒频率扩展，从而造成大量杂波进入雷达数据处理单元。为了降低杂波对模型估计的影响，需要对量测进行正确的数据关联，典型的关联方法是PDA。

传统PDA中互联概率的计算只是利用了杂波和目标量测在位置信息上的不同。杂波和目标量测的另一不同之处是从统计意义上目标回波的幅度均值高于杂波的幅度均值。据此，文献[16]提出了AI-PDA，本文将其应用于速度拖引干扰和杂波背景下的数据关联，以降低杂波对目标跟踪的不良影响。下面只给出双模型结构中模型M1基于AI-PDA的数据关联和滤波估计结果，模型M2的数据关联和滤波估计结果可同理得到，具体步骤见文献[16]。

k时刻落入相关波门内所有量测中第i个量测的互联概率为

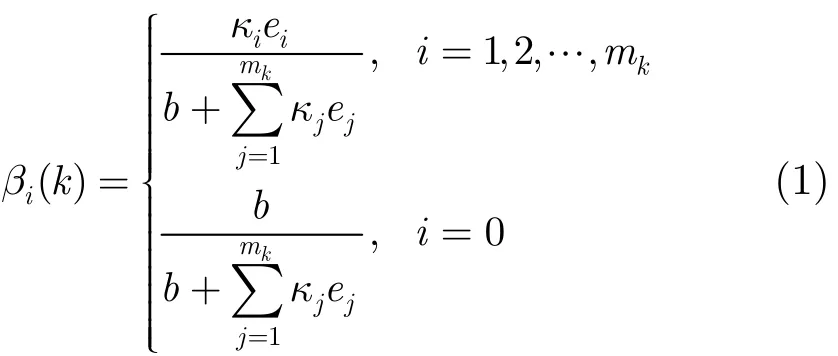
其中，β0(k)表示没有量测源于目标的概率，b=λ |2πSi(k)|1/2(1−PDPG)/PD,ei=exp[−0.5(k)S(k ) vi(k)],PD为目标检测概率，PG为门概率，vi(k)和Si(k)分别为第i个量测对应的新息和新息协方差，λ为杂波的空间密度，κi为幅度似然比，可由幅度条件概率密度的比值得到[16]

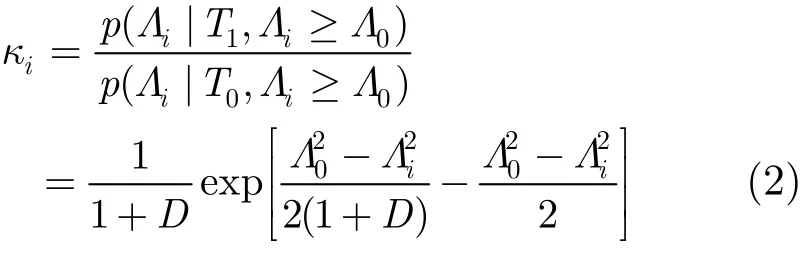
其中，iΛ为第i个量测对应的信号幅度，Λ0为信号检测器门限，T1表示该量测是目标量测，T0表示该量测是杂波，D为目标信号功率的均值，可使用α估计器进行估计。

k时刻模型M1的目标状态估计为

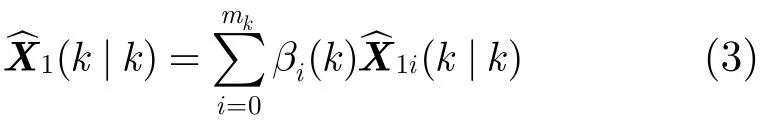
如果相关波门内没有量测，即事件θ0(k)成立，则用预测值替代估计值，即

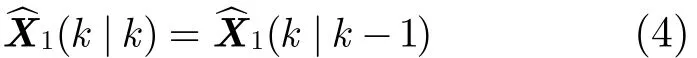
与估计值相对应的估计误差协方差为

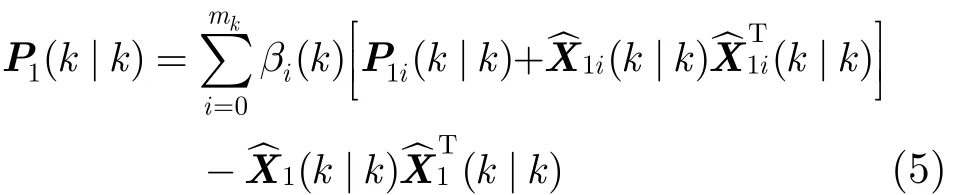
其中，P1i(k|k)为模型M1中第i个量测对应的估计误差协方差。

同理，可得模型M2的目标状态估计ˆ2(k|k) X和对应的估计误差协方差P2(k|k)。

2.3 模型选择

设k时刻目标的状态为X(k)，根据上一节可得到模型M1估计出的目标状态为1(k|k)，其对应的估计误差协方差为P1(k|k)，模型M2估计出的目标状态为2(k|k)，其对应的估计误差协方差为P2(k|k)。

如果雷达没有受到速度拖引干扰，则空间位置量测和径向速度量测都是真实的，可近似认为

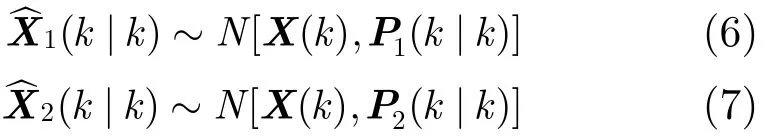
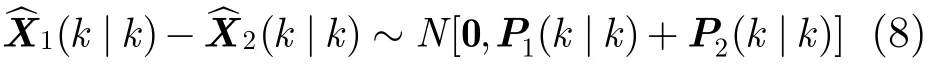
其中，0表示零向量，N[A,B]表示以A为均值，以B为协方差的多元正态分布。

如果雷达受到速度拖引干扰，则径向速度量测是虚假的，而空间位置量测是真实的，可近似认为

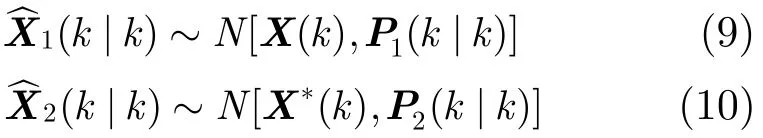
其中，X∗(k)是不等于X(k)的不确定向量。进而可得

根据以上分析，建立的假设为

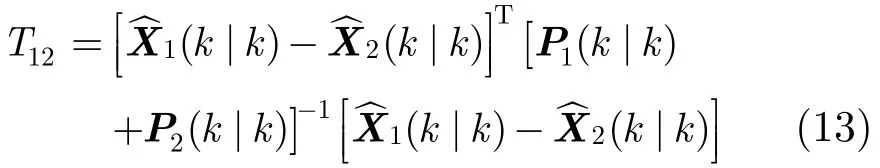
构造的检验统计量为

利用T12对式(12)中的假设进行检验，其单侧拒绝域为

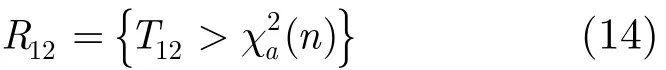
在k时刻，对模型M1和模型M2的估计结果进行上述检验。

若T12＜(n)，接受假设H0，则认为两个模型估计结果差异较小，此时没有速度拖引干扰，两个模型均能对目标状态进行正确估计，而模型M2的估计精度更高，最终的目标状态估计值取模型M2的结果，即

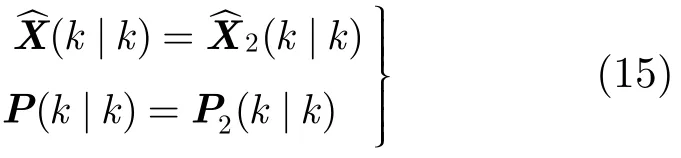
若T12＞(n)，接受假设H1，则认为两个模型估计的结果差异较大，而造成这种差异的原因主要有

(1)速度拖引干扰使模型M2滤波发散或估计误差增大；

(2)目标机动使两个模型滤波出现不同程度的发散或其中某个模型的估计误差增大。

在实际应用中，模型的估计误差是无法确定的，只能通过判断模型的发散程度来确定选取哪一个模型的估计结果。假设目标状态估计误差协方差阵的第(1,1), (3,3), (5,5)个元素分别是目标x轴，y轴，z轴位置估计误差的方差，则构建的控制量为

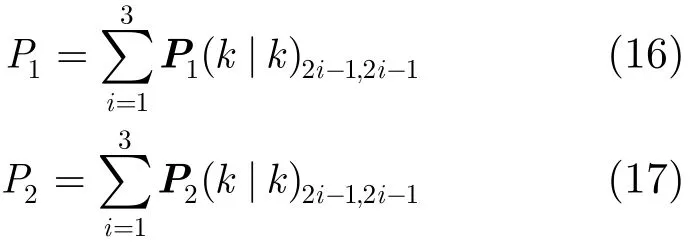
若T12＞(n)且P1＞P2，则认为模型M1发散程度高，最终的目标状态估计取模型M2的结果，即式(15)。

若T12＞(n)且P1＜P2，则认为模型M2的发散程度高，最终的目标状态估计值取模型M1的结果，即

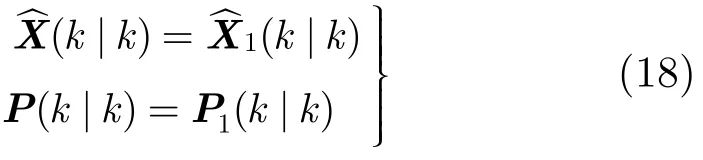
模型选择规则的框图如图2所示。

3 仿真与分析

3.1 仿真背景

以一部机载PD雷达和一架携带自卫式欺骗干扰机的飞行目标为仿真背景，建立统一的直角坐标系。雷达载机匀速直线运动，初始位置为(0 km, 0 km, 6 km)，速度为(150 m/s, 0 m/s, 0 m/s)，雷达扫描周期为0.1 s，测距误差为100 m，测方位角误差和测俯仰角误差均为0.1°，测速误差为5 m/s，恒虚警率为Pfa=0.001。目标初始位置为(60 km, 50 km, 3 km)，初始速度为(-200 m/s, 100 m/s, 0 m/s)，目标匀速飞行10 s后做转弯机动，加速度为(20 m/s2, 20 m/s2, 0 m/s2)，机动持续10 s，然后改匀速飞行10 s，再做加速度为(-20 m/s2, -20 m/s2, 0 m/s2)的转弯机动，机动持续10 s，最后保持匀速飞行，整个飞行过程持续60 s，过程噪声的方差为100。

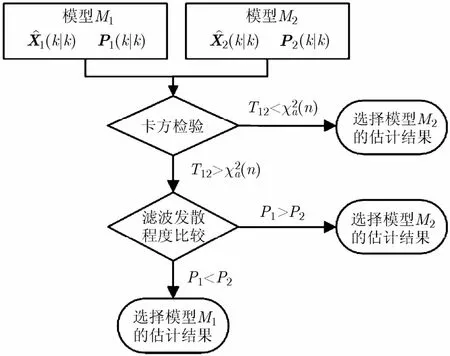
图2 模型选择规则框图

3.2 仿真实验1

本实验的目的是验证在没有速度拖引干扰的杂波环境下，基于DM-AI的目标跟踪算法能稳定跟踪目标，幅度信息能有效克服杂波的影响，提高目标跟踪精度。设杂波密度λ=2×10−5个/m3，加入杂波的方法见文献[18]，目标信噪比均值为10 dB。蒙特卡洛仿真次数为100次，分别得到本文算法和基于空间位置加径向速度量测而不带幅度信息的PDACA-CMKF的目标位置均方根误差，如图3所示。

从图3可以看出，由于目标机动和杂波的影响，PDA-CA-CMKF的跟踪精度出现了较大波动，而本文算法的跟踪性能较为稳定，跟踪精度高于PDACA-CMKF，也即证明了幅度信息能显著提高杂波环境下目标跟踪性能。在双模型结构中，模型M1运用的算法是基于空间位置量测的AI-PDA-CACMKF，模型M2运用的算法是基于空间位置和速度量测的AI-PDA-CA-CMKF。

进行单次仿真，分别得到双模型结构中模型M1和模型M2及双模型结构(即本文所提的基于DM-AI的跟踪模型)滤波的位置均方根误差，如图4所示。

图4表明，模型M2的滤波误差要小于模型M1，双模型结构的滤波误差与模型M2几乎相同，从而证明了在无速度拖引干扰的情况下，本文所提的基于DM-AI的跟踪算法能自动选择精度更高的模型M2进行滤波。

3.3 仿真实验2

本实验的目的是验证在速度拖引干扰和杂波背景下，本文算法能有效地抑制虚假速度量测对目标跟踪的不良影响，防止滤波发散，能稳定跟踪目标。以指向雷达的方向为正，设目标在第10 s开始施放20 m/s2的径向速度拖引干扰，持续10 s，在第30 s开始施放-20 m/s2的径向速度拖引干扰，同样持续10 s。显著性水平取a=0.005，其它条件与实验1相同。通过仿真，分别得到本文算法、基于空间位置和速度量测且带幅度信息的AI-PDA-CA-CMKF的位置均方根误差，如图5所示。

图5表明，在无速度拖引干扰时，本文算法的跟踪误差与带幅度信息和速度量测的AI-PDA-CACMKF相当，而出现速度拖引干扰后，本文算法的跟踪误差明显小于带幅度信息和速度量测的AIPDA-CA-CMKF。

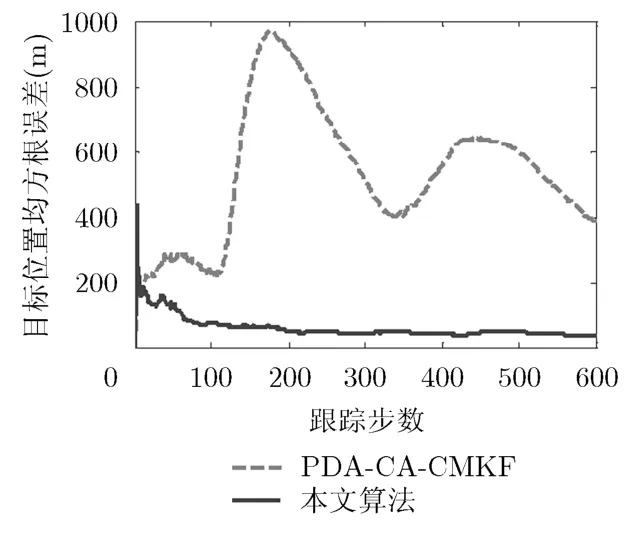
图3 两种算法的目标位置均方根误差比较

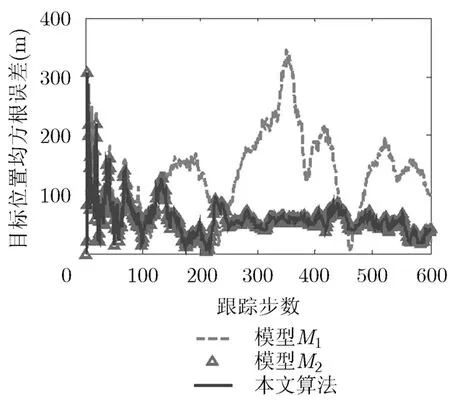
图4 模型M1，模型M2和双模型结构的目标位置均方根误差比较

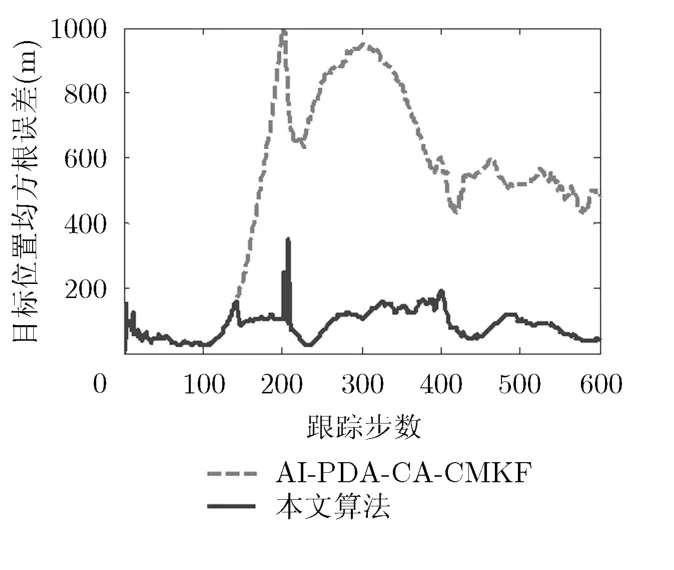
图5 两种算法的目标位置均方根误差比较

进行单次仿真，分别得到双模型结构中模型M1和模型M2及双模型结构滤波的位置均方根误差，如图6所示。

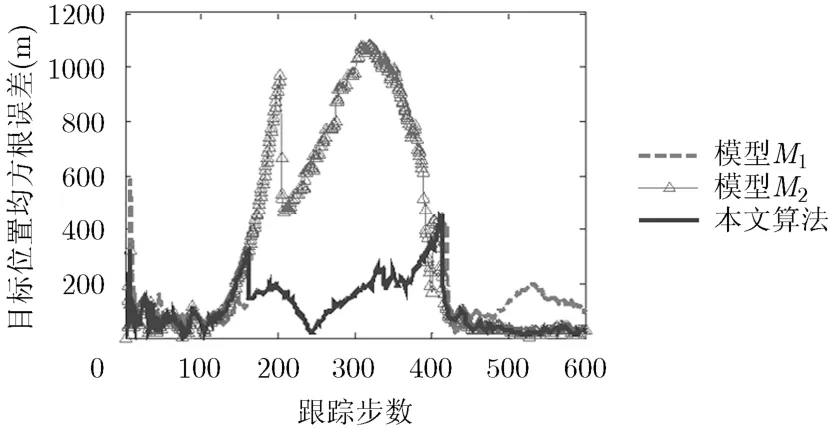
图6 模型M1，模型M2和双模型结构的目标位置均方根误差比较

图6表明，在速度拖引干扰的情况下，模型M2的滤波误差明显大于模型M1，双模型结构自动选择误差较小的模型M1进行滤波，而当速度拖引干扰结束后，模型M2的滤波误差逐渐减小至模型M1的滤波误差以下，双模型结构自动选择误差较小的模型M2进行滤波，从而证明了双模型结构具有较强的自适应性。

3.4 仿真实验3

为了进一步分析本文算法的性能，对不同杂波密度的情况进行了仿真，在航迹丢失率和时效方面与经典的速度比较法进行对比。在目标跟踪过程中，以相关波门内没有目标量测或没有量测源于目标的互联概率β0≥0.9连续超过3次作为航迹丢失的标志。设置杂波密度分别为λ=1×10−6个/m3和1×10−5个/m3，目标信噪比的均值为10 dB。速度比较法先利用基于空间位置和速度量测的CA-EKF进行跟踪，估计出航迹速度，然后进行航迹估计速度和量测速度的检验比较，显著性水平取a=0.005，当检验结果为不存在速度拖引干扰时进行下一时刻滤波更新，而检验结果为存在速度拖引干扰时采用空间位置量测进行二次滤波。其它仿真条件同仿真实验1和实验2。仿真使用的计算机为：Intel Dual-Core E6500 2.93 GHz CPU和2GB RAM。仿真结果如表1所示。

由表1可知，当杂波密度一定，无速度拖引干扰时，本文算法和速度比较法的航迹丢失率相当，在时耗上本文算法高于速度比较法约50%；存在速度拖引干扰时，本文算法的航迹丢失率明显低于速度比较法，而在时耗上本文算法也低于速度比较法约20%。这是因为，在无速度拖引干扰时，本文算法是用双模型进行滤波的，而速度比较法用的是单模型，存在速度拖引干扰时，速度比较法也需要进行二次滤波。随着杂波密度的增大，两种算法的航迹丢失率和时耗均有增加，而速度比较法的时耗增加幅度更大，这是因为速度比较法不仅在滤波时受杂波影响，而且在进行速度检验比较时所有杂波也要参与运算，而本文算法只在滤波时受杂波影响，进行模型选择时只有两个模型的滤波结果参与运算。

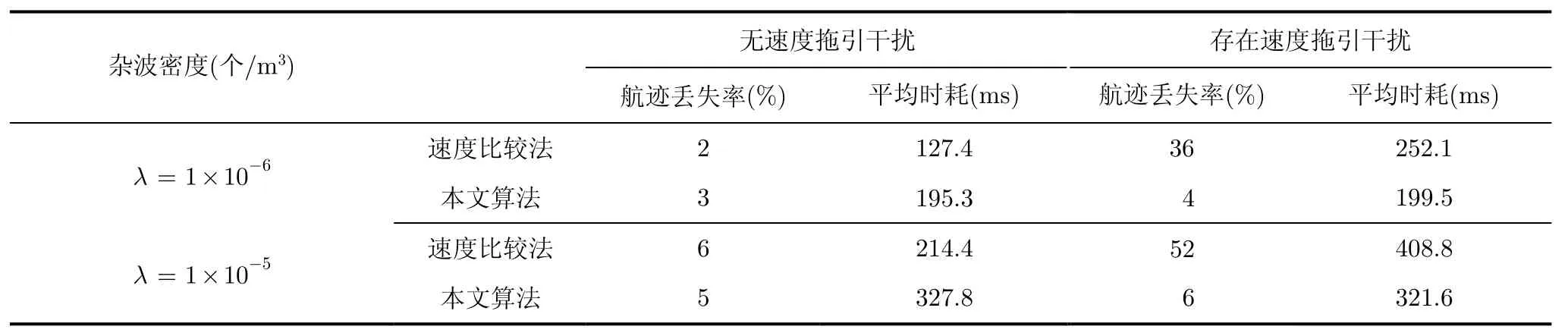
表1 本文算法和速度比较法分别在航迹丢失率和平均时耗方面的对比

4 结束语

本文针对速度拖引干扰和杂波背景下PD雷达无法稳定跟踪目标的问题，提出了基于DM-AI的目标跟踪算法。该算法运用基于幅度信息的PDA，克服了大量杂波对目标跟踪的不良影响。算法建立了基于不同量测集合的双模型，构建了用于选择模型输出的检验统计量，通过卡方检验灵活控制选择最终的目标状态估计，实现了在无速度拖引干扰时其跟踪精度与带速度量测的目标跟踪算法的跟踪精度相当，在速度拖引干扰和杂波背景下能对目标稳定跟踪，算法具有较强的自适应能力。仿真结果验证了该算法的有效性。

[1] 王小谟, 张光义. 雷达与探测[M]. 第2版, 北京: 国防工业出版社, 2008: 114-120.

Wang Xiao-mo and Zhang Guang-yi. Radar and Detection [M]. Second Edtion, Beijing: National Defence Industry Press, 2008: 114-120.

[2] Butt F A and Jalil M. An overview of electronic warfare in radar systems[C]. Proceedings of the IEEE International Conference on Technological Advances in Electrical, Electronics and Computer Engineering, Konya, Turkey, 2013: 213-217.

[3] Bar-Shalom Y and Blair W D. Multitarget-Multisensor Tracking Applications and Advances .Volume Ⅲ[M].Boston, London: Artech House, 2000: 395-458.

[4] Akhtar J. Orthogonal block coded ECCM schemes against repeat radar jammers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1218-1226.

[5] Zhang Jing-dong, Zhu Dai-yin, and Gong Zhang. New antivelocity deception jamming technique using pulses with adaptive initial phases[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290-1300.

[6] Greco M, Gini F, and Farina A. Radar detection and classification of jamming signals belong to a cone class[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 1984-1993.

[7] Bandiera F, Farina A, Orlando D, et al.. Detection algorithms to discriminate between radar targets and ECM signals[J]. IEEE Transactions on Signal Processing, 2010, 58(12): 5984-5993.

[8] 陈建春, 耿富录. 基于线性预测滤波的抗速度欺骗干扰技术[J]. 系统工程与电子技术, 2002, 24(2): 22-24.

Chen Jian-chun and Geng Fu-lu. Anti-velocity deception jamming technique based on linear prediction error filtering[J]. Systems Engineering and Electronics, 2002, 24(2): 22-24.

[9] 卢云龙, 李明, 闫琰. 一种利用调频率匹配的DRFM欺骗干扰检测方法[J]. 西安电子科技大学学报, 2014, 41(5): 77-84.

Lu Yun-long, Li Ming, and Yan Yan. Method for detecting DRFM deception jamming based on LFM rate matching[J]. Journal of XiDian University, 2014, 41(5): 77-84.

[10] Tian Xiao and Tang Bin. Spectrum texture features based radar deception jamming recognition using joint frequency-slow time processing[J]. Journal of Information & Computational Science, 2013, 9(13): 5181-5188.

[11] Berger S D. Digital radio frequency memory linear range gate stealer spectrum[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(2): 725-735.

[12] Tian Xiao. Radar deceptive jamming detection based on goodness-of-fit testing[J]. Journal of Information & Computational Science, 2012, 9(13): 3839-3847.

[13] 赵博, 周峰, 保铮. 基于电磁散射模型的ISAR空中目标欺骗干扰方法[J]. 电子与信息学报, 2014, 36(1): 194-201.

Zhao Bo, Zhou Feng, and Bao Zheng. Deception jamming for ISAR aerial target based on electromagnetic scattering model[J]. Journal of Electronics & Information Technology, 2014, 36(1): 194-201.

[14] 贲德. 机载脉冲多普勒(PD)雷达的工作特点及抗干扰措施[J].现代雷达, 2000(4): 1-6.

Ben De. The property of airborne pulsed Doppler radar and the methods of counter countermeasures[J]. Modern Radar, 2000(4): 1-6.

[15] 李淑华, 黄晓刚, 刘平. 复杂电磁环境下雷达抗干扰技术研究[J]. 现代雷达, 2013, 35(4): 1-9.

Li Shu-hua, Huang Xiao-gang, and Liu Ping. A study on radar anti-jamming technology under complex electromagnetic environment[J]. Modern Radar, 2013, 35(4): 1-9.

[16] Lerro D and Bar-Shalom Y. Interacting multiple model tracking with target amplitude feature[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(2): 494-509.

[17] Bar-Shalom Y and Fortmann T E. Tracking and Data Association[M]. Salt Lake City: Academic Press, 1988: 297-298.

[18] 何友, 修建娟, 关欣, 等. 雷达数据处理及应用[M]. 第3版,北京: 电子工业出版社, 2013: 147-155.

He You, Xiu Jian-juan, Guan Xin, et al.. Radar Data Processing with Applications[M]. Third Edtion, Beijing: Publishing House of Electronics Industry, 2013: 147-155.

李迎春： 男，1988年生，博士生，研究方向为雷达抗干扰技术、多传感器融合技术.

王国宏： 男，1963年生，博士生导师，教授，研究方向为多源信息融合、雷达组网、微弱目标跟踪、系统误差配准等.

关成斌： 男，1979年生，硕士，讲师，研究方向为信息融合、目标跟踪、传感器管理.

孙殿星： 男，1983年生，博士生，研究方向为雷达组网、信息融合技术等.

Algorithm for Target Tracking with Pulse Doppler Radar in the Presence of Velocity Gate Pull off/in Jamming and Clutter Environment

Li Ying-chun Wang Guo-hong Guan Cheng-bin Sun Dian-xing
(Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China)

Considering the problem that Pulse Doppler (PD) radar is not able to track target precisely in the presence of velocity gate pull-off/in jamming and clutter environment, an algorithm for target tracking is proposed which is based on the Double Models (DM) and the Amplitude Information (AI). The algorithm establishes two tracking models: one model is based on the position and amplitude measurements, the other is based on the position, velocity, and amplitude measurements. The two models both use Probabilistic Data Association based on AI (AI-PDA) to reduce the influence of clutter as much as possible, then carry out filtering and estimating using the conventional method. If there is no velocity gate pull off/in jamming, the estimations of two models are related on position and velocity; if there is jamming, the estimations are not related. Accordingly, the chi-square test is carried out and the final estimation result is determined after analysis. The simulation results prove the effectiveness of the algorithm.

Radar; Target tracking; Velocity gate pull-off/in jamming; Double Models (DM); Amplitude Information (AI); Chi-square test

TN953

： A

：1009-5896(2015)04-0989-06

10.11999/JEIT140856

2014-06-26收到，2014-12-04改回

国家自然科学基金(61179018, 61102165)和“泰山学者”建设工程专项经费资助课题

*通信作者：李迎春 344759609@qq.com