基于人工蜂群PID的永磁同步电机调速系统
蔡超,周武能,2
(1.东华大学信息科学与技术学院,上海201620;2.数字化纺织服装技术教育部工程研究中心,上海201620)
永磁同步电机(PMSM)以其体积小,转矩脉动小,功率密度高等优点,广泛应用于工业机器人、数控机床、航空航天等领域[1]。矢量控制策略的应用使得永磁同步电机控制性能进一步提高,矢量控制系统常采用PID 控制器进行调节,PID控制器具有算法简单,鲁棒性好,可靠性高等优点,已经广泛应用于工业过程控制[2]。目前,过程控制中仍有84%采用纯PID 调节器,若包含改进型则超过90%。
人工智能技术的出现为PID控制器的参数自整定开辟了一条新路,目前已经出现了基于知识推理的专家PID 控制、基于模糊逻辑的智能PID控制、基于连接机制的神经网络PID控制、基于遗传算法的PID控制[3]。这些控制策略或要求对被控对象和控制规律有全面的先验知识,或要求搜索空间为具有连续导数的光滑空间,具有一定的应用局限性。
人工蜂群算法(ABC)是一种最新发展的模拟蜜蜂群体寻找优良蜜源的仿生智能进化算法。它由土耳其学者Karaboga 于2005 年提出,与粒子群算法、遗传算法等智能算法相比,该算法的突出优点是在每次迭代过程中都进行全局和局部搜索,不易陷入局部最优,且易收敛[4]。Karaboga 等已经成功将人工蜂群算法应用于神经网络训练[5],无人机航路规划[6],任务调度优化[7],图像处理[8]等领域。鉴于该算法的应用不断取得成功,本文将人工蜂群算法与PID控制器相结合,并应用到PMSM速度环调节器中,以使PMSM交流伺服系统获得更好的控制性能。
1 永磁同步电机的数学模型
PMSM 的定子和普通电励磁三相同步电机的定子相似,在建模分析时常做以下假设:定子和转子磁动势所产生的磁场沿定子内圆正弦分布;不计铁心涡流与磁滞损耗;忽略定子铁心饱和;转子上没有阻尼绕组。在d-q旋转坐标系下,建立永磁同步电机数学模型,其定子电压方程为
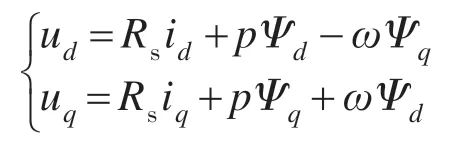
磁链方程为
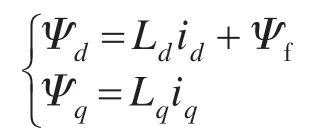
式中:ud,uq为定子电压d,q轴分量;id,iq为定子电流d,q 轴分量;ω为转子角速度;p为电机的极对数;Rs为定子绕组电阻;Ψd,Ψq为定子磁链d,q 轴分量;Ld,Lq为定子直轴、交轴电感;Ψf为永磁体与定子交链的磁链。
电磁转矩方程

机械运动方程
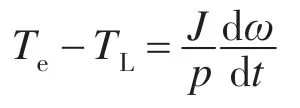
式中:Te为电磁转矩;TL为负载转矩;J 为转动惯量。
2 永磁交流伺服系统结构
交流伺服系统以永磁同步电机为被控对象,通过矢量控制方法对电流进行解耦,应用电压空间矢量技术(SVPWM)生成脉宽调制波,输出到逆变器进而驱动电机运转。控制系统采用电流环内环,速度环外环的双闭环控制方式。为了提高速度调节性能,增强系统鲁棒性,外环即速度环改由人工蜂群优化PID 控制器代替传统PID,良好的速度外环可以抑制系统干扰和补偿内环扰动。采用id*=0控制方式的永磁同步电机矢量控制系统结构如图1所示。

图1 永磁同步电机控制系统结构Fig.1 Diagram of PMSM control system
3 人工蜂群优化PID控制器
3.1 人工蜂群优化算法
人工蜂群算法的思想来源于昆虫王国中蜜蜂的觅食行为,蜜蜂同具体的蜜源联系在一起,蜜源即为解空间内的所有可能解。将蜜蜂种群分为3种类型,即引领蜂、跟随蜂、侦查蜂,这3种角色之间具有特定的转变机制。蜂群对蜜源的搜索过程为:1)引领蜂和具体的蜜源联系在一起,其发现蜜源,并通过摇摆舞分享蜜源信息;2)跟随蜂根据引领蜂所分享的信息选择一个蜜源,并在其附近进行采蜜,寻找新蜜源,若搜索到更高适应度的蜜源,则跟随蜂转变为引领蜂;3)引领蜂在其前次搜索到的蜜源邻域附近进行多次搜索,当多次搜索仍未找到更高适应度的蜜源时,则放弃该蜜源,转变为侦查蜂,随机搜索新蜜源,当其搜索到高适应度的蜜源时又转变为引领蜂[9]。
假设求解问题的空间维度为D,蜜蜂种群代数为n,蜜蜂总数为NA,其中引领蜂规模为NG,跟随蜂规模为NF,一般取NG=NF,在搜索开始阶段,随机生成NA个蜜源,即初始解(X1,X2’···,XNA),且
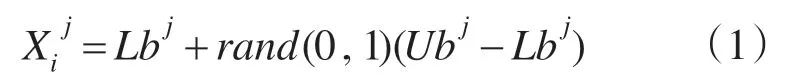
式中:Ub,Lb分别为搜索空间的上下限;j为被优化参数组成的D 维解向量的某个分量,j ∈{1’2’···,D}。
再计算各个解的适应度,将排名前NG的解作为初始代引领蜂种群X(0),对于第n代的引领蜂Xi(n),i ∈{1’2’···,NG},在蜜源i位置进行邻域搜索,即
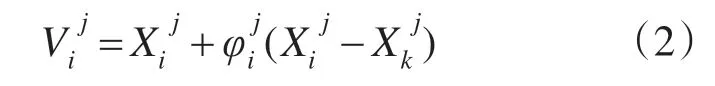
其中j 是在[1’D]内的一个随机整数,表示引领蜂随机选择某一维进行搜索,k ∈{1’2’···,NG},k随机生成且k ≠j,φji 为[-1’1]之间的随机数,且须保证生成的V在解空间内,采用贪婪选择法在蜜源Vi和Xi中选取较优适应度的蜜源保留至下一代种群,当所有引领蜂完成式(2)的搜索后将蜜源信息共享,接着,各跟随蜂按照引领蜂种群适应度值选择一个引领蜂,并同样对其邻域进行搜索,选择概率为

式中:f(Xi)为第i个蜜源的适应度值。
若某只引领蜂在其周围搜索次数times 达到一定阈值Limit仍未找到更优解,则放弃该蜜源,对应的引领蜂转变为侦查蜂,同时重新初始化该引领蜂对应的蜜源,即

3.2 ABC-PID控制器设计
ABC-PID控制器的结构如图2所示,控制器主要分为2 个部分:一部分为ABC 算法,如虚线框内所示,另一部分为传统PID 控制器。两者通过适应度函数结合起来。

图2 ABC-PID控制器结构Fig.2 Diagram of ABC-PID controller
将待优化参数Kp,Ki和Kd的某一组值看作一个蜜源,将这3个参数的取值范围看作蜂群的搜索空间,利用蜂群算法的搜索机制寻找最优控制参数,而评价参数是否最优须由适应度函数来确定,适应度函数即用来评价蜜源质量的好坏。本设计中评价参数是否最优是根据在该参数下PMSM调速系统的速度响应情况而定的,为了让控制器对PMSM具备优秀的调速性能,即能够快速地跟踪给定速度并且无超调,本文选取伺服控制系统设计中最常用也是最直观的指标,即时间乘以误差绝对值积分(ITAE)作为评价函数[10],其表达式为

式中:t为时间;e(t)为速度误差。
此外,为了避免超调,引入超调惩罚项βMp,从而使评价函数转变为
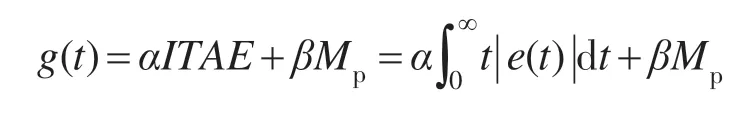
式中:α,β为惩罚权值;Mp为系统超调量。
参数寻优的目的是使评价函数g(t)最小,而人工蜂群算法在搜索时总是向更高适应度的方向进行,因此,取适应度函数为评价函数的倒数,即

从而引导蜜蜂种群搜索最优参数组合,使得整个调速系统取得良好的动静态性能。
3.3 算法实现步骤
采用人工蜂群算法优化PMSM 调速系统的具体实现步骤如下:
1)初始化蜂群种群规模NA,设定最大迭代次数Cycle和最大搜索阈值Limit,并确定3个控制参数Kp,Ki和Kd的取值范围;
2)迭代次数n=1,按式(1)初始化蜜源Xi,对每个蜜源,采用罗斯-霍尔维茨准则判断闭环系统稳定性,并根据式(5)计算其适应度值,同时将蜜蜂分为引领蜂和跟随蜂;
3)每只引领蜂在原蜜源附近采蜜,按式(2)寻找新蜜源,并按贪婪选择机制进行更新;
4)由式(3)计算引领蜂搜索到的蜜源被跟随的概率;
5)跟随蜂按照与引领蜂相同的方式进行搜索,并按贪婪选择法保留更优蜜源;
6)若某只引领蜂搜索次数达Limit仍未找到更高适应度的蜜源,则放弃该蜜源,转变为侦查蜂,并按式(4)重新产生一个新蜜源;
7)记录最优解及其适应度值,n=n+1,跳转至步骤2,重复运行,直至最大迭代次数Cycle,并输出PID控制器最优参数及最优适应度值。
4 实验及结果分析
为验证算法的可行性,根据图1 在Matlab/Simulink 环境中搭建PMSM 双闭环调速系统模型,并用ABC-PID控制器取代传统PID控制器施加到矢量控制的速度环中。永磁同步电机参数为:额定功率P=1.5 kW;额定转矩Tn=10 N·m;定子电阻R=0.4 Ω;定子电感L=0.85 mH;极对数p=4;转动惯量J=9 kg·cm2。
算法参数设置为:蜂群进化代数Cycle=50;解空间维度D=3;蜂群规模NA=20;搜索阈值Limit=80;适应度函数中的惩罚权值分别取α=5,β=1。给定电机转速800 r/min进行动态仿真,经过50代进化后,人工蜂群算法收敛并搜索到控制器最优参数为Kp=10.886 1,Ki=81.529 2,Kd=0.006 5,其最优适应度值为95.24,其中ITAE=0.001 6,Mp=0.25%。
对比本文提出的ABC-PID 控制器和传统PID 控制器,对两种方法所得到的电机速度响应结果进行比较。
图3 为给定转速800 r/min 时PMSM 阶跃速度响应情况,从图3 中可以看出,ABC-PID 控制器调节时间ts(Δ=0.02)更短,为0.002 9 s,且几乎无超调,稳态误差也很小,其稳态误差为1 r/min,而传统PID控制器超调量较大,且调节时间较长,不能及时准确地达到阶跃给定信号。

图3 阶跃速度给定PMSM速度响应Fig.3 Speed response of PMSM with step speed desired
为了进一步验证所提方法对速度参数的变化是否敏感,给定电机转速为-1 000 r/min 和+1 000 r/min 之间突变的方波信号,其周期为0.1 s。图4a和图4b分别为ABC-PID控制和传统PID 控制下PMSM 的速度响应结果,由图4 中波形可以看出,给定转速突变时ABC-PID 控制器仍能快速地跟踪给定信号,几乎无超调,而传统PID 控制器要经过较长时间才能恢复到给定,且超调量较大,无法快速准确地跟随给定信号。

图4 10 Hz方波速度给定时PMSM速度响应Fig.4 Speed response of PMSM with 10 Hz square speed desired
5 结论
本文设计了基于人工蜂群算法的PID 控制器,将其替代传统PID控制器应用在PMSM控制系统的速度环中,该系统采用矢量控制策略,电流环仍为传统PI 调节器。为了实现对给定速度快速且无超调地跟踪,设计了相应的适应度函数,将被优化参数看作蜜源,充分利用人工蜂群算法特有的角色转变机制和寻优机制搜索最优控制器参数,较好地解决了永磁同步电机高性能的速度控制问题。相比传统PID 控制器,人工蜂群PID参数自整定控制器具有更好的动态性能和静态性能,是一种行之有效的控制方案。
[1]刘贤兴,卜言柱,胡育文,等.基于精确线性化解耦的永磁同步电机空间矢量调制系统[J]. 中国电机工程学报,2007,27(30):55-59.
[2]王强,钱敏,陈军,等.改进型免疫算法PID设计及在调速系统中的应用[J].电气传动,2009,39(2):56-60.
[3]任志斌,谢阳萍,肖宇连.基于粒子群算法的永磁同步电机控制系统研制[J].微电机,2013,46(12):39-41.
[4]HU C L,SUN T Y.Reliable Multi-goal Route Planning for Vehicle Using Skeletonization and Genetic Algorithms[C]//Proc 2008 CACS International Automatic Control Conference,2008:159-163.
[5]Karaboga D,Akay B,Ozturk C.Artificial Bee Colony Optimization Algorithm for Training Feed Forward Neural Networks[C]// Proceeding of Modeling Decisions for Artificial Intelligence Conference,2007:318-319.
[6]刘敏,邹杰,冯星,等.人工蜂群算法的无人机航路规划与平滑[J].智能系统学报,2011,6(4):344-349.
[7]王浩,汤再江,范锐.蜂群算法在装备维修任务调度中的应用[J].计算机工程,2010,36(7):242-245.
[8]Duan H B,XU C F,Xing Z H.A Hybrid Artificial Bee Colony Optimization and Quantum Evolutionary Algorithm for Continuous Optimization Problems[J]. International Journal of Neural Systems,2010,20(1):39-50.
[9]段海滨,张祥银,徐春芳.仿生智能计算[M].北京:科学出版社,2011.
[10]史婷娜,张典林,夏长亮,等.基于遗传整定的永磁交流伺服系统模糊免疫PID 控制器[J].电工技术学报,2008,23(7):45-49.

