基于小波的局部放电信号去噪算法研究
姚勇 马杰 刘璐璐
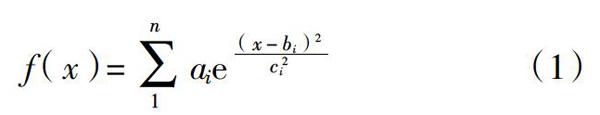

摘要:针对因脉冲型信号和放电信号的时域频域特征非常相近导致抑制脉冲型非常困难的情况,提出一个基于小波的干扰抑制方法。该方法可以在随机脉冲信号、手机信号和白噪声等干扰信号和局部信号耦合的情况下,分离出局放信号,从而对局部放电测量提供有效的数据和有利的保障,并通过仿真和现场试验共同验证提出算法的有效性。
关键词:超高压输电线路;小波变换;多尺度信号分析;局部放电识别;时频分析
文献标志码:A 文章编号:1674-5124(2015)01-0037-03
0引言
局部放电(partial discharge,PD)是引发气体绝缘组合电器(gas insulated switchgear,GIS)故障的重要因素之一;因此,必须对GIS中PD进行监测和分析,得到典型的局部放电类型,从而避免事故的发生。典型的测试流程分为去噪、多源信号分离、特征提取和特征识别等阶段。噪声、干扰的消除是有效识别GIS局部放电类型、监测GIS故障的前提。主要的外部干扰由3部分组成:1)周期性干扰,来自无线通信信号、雷达信号和电力线载波通信系统等;2)随机脉冲型干扰,来自随机的开关操作、雷电或者发动机;3)白噪声,源于设备本身的热噪声。
通常这些外部干扰会带来错误的指示,从而降低PD监测的可信度;这个问题也引起了人们广泛的关注并提出了许多解决方案,如窄带信号监测技术和脉冲捕获电路。但是,这些模拟电路的手段往往比较复杂并且需要较高的适应性。由于现场情况复杂,需要测试人员根据具体情况不断调节参数,降低了局放监测系统的可操作性。另一方面,随着数字技术的兴起,滤波技术逐渐转向数字域,对PD信号的数字滤波也引起了人们广泛的关注,如平滑滤波方法、FFF门限方法圈、数字滤波器方法(无限冲击响应(IIR)和有限冲击响应(FIR))、适应滤波器等。然而,上述方案主要用于消除正弦型窄带干扰信号,对于脉冲型信号并不适用。即使针对有周期特性的方波信号,如无线通信干扰信号(手机),这些方法虽然能够从一定程度上抑制信号的能量,但是残留的高频谐波分量往往带来巨大的误差。
在上述外部干扰中,周期性窄带干扰可以在频域中被识别出来,周期性脉冲型干扰从一定程度上可以在时域识别并且消除(主要由于时间的周期性和持续时间的稳定性);但是,随机的脉冲型干扰和白噪声就需要时域频域的联合分析。小波分析是强有力的时频分析工具,并且在干扰消除方面应用广泛。本文提出了利用小波消除各种类型干扰的方法,从而提取出有效的PD信号;并通过仿真和现场应用共同验证了该方案的有效性。
1基于小波的除噪方案
传统的基于小波的除噪方案首先计算一个给定信号的DWT系数,然后通过一个预设的门限传递给DWT,最后根据修改的DWT系数进行反向小波变换重构,这个方法通常叫做硬或者软门限。然而,许多文献已经证实,这种方案很难在PD除噪过程中应用,主要因为很难仅仅通过检查DWT系数来给定门限的值。
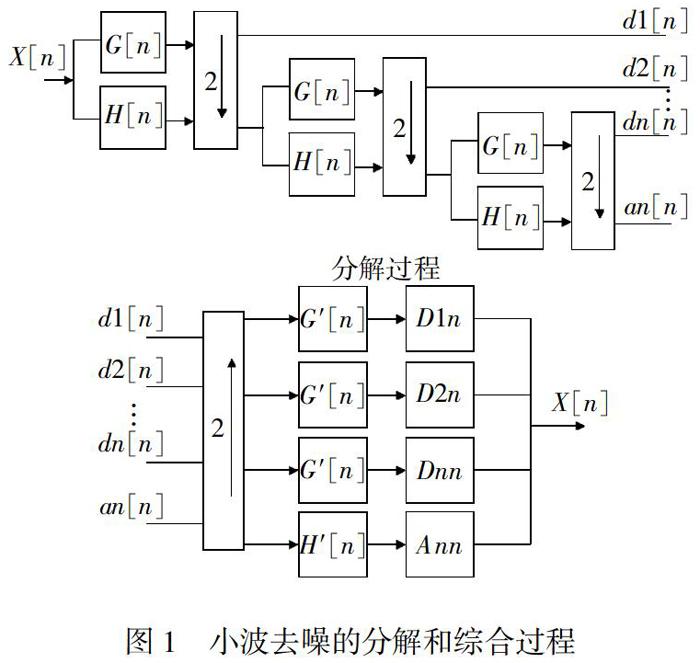
本文提出的方案通过时域和频域的联合分析来抑制干扰,具有低处理时间和更好的重构特性。干扰抑制分为两个阶段。首先,输入信号通过多尺度分析分解为一定层次的近似和细节部分;一旦母小波给定,分解和重构过程仅仅通过母小波的平移和伸缩操作;分解和重构层次数目的选择可以通过简单的尝试错误方法或者通过采用频率信息。每个分解成分遵循奈奎斯特采样定理。图1为分析和综合的方法。
一旦计算出了近似和细节的重构时域部分,开始进入第2阶段,识别这些成分相应的干扰部分。这一阶段主要根据已知PD的带宽信息来排除干扰信号。最终,通过消除所有识别的干扰成分得以获取去噪后的信号。综上,基于小波的去噪方案总结如下:
1)选择一个母小波,将输入信号(PD和干扰混合的信号)分解为M层次,同时产生DWT系数。
2)不同于其他方法,在本方案中,这些DWT系数重构成M层次时域序列,每个长度都等于原始的信号长度,每一个这样的层次,相当于一段非重叠的频段。将这些M层次进行加和就得到了原始的信号,如此获得输入信号的联合时频表达。
3)根据采样频率和分解的层次,定位PD信号,从而滤除不必要的干扰。
2仿真验证
首先对上述算法进行仿真验证。仿真软件采用Matlab,小波信号采用高斯函数拟合的方法,函数表达式为式中n为脉冲极值的个数,一般n=3~5。
本文取n=4并且具体系数根据文献选择,这样得到的仿真脉冲信号如图2所示。
背景噪声采用白噪声生成函数产生,干扰信号由多个正弦谐波加和产生。在1000个采样点中,模拟频率为1 000,800,720,660,500,450,300,200MHz的正弦信号的加和。PD信号的采用点数为25,也就是频率最小的信号周期为PD信号持续时间的8倍。PD信号在1000个采样点中随机出现10次。这样输入信号的波形如图3所示。
滤波后的波形如图4所示,通过滤波前后可以比较本算法的效能。另外,对算法的有效性进行了定量分析。
去噪过程中,在滤除噪声成分的同时,和干扰相近的PD信号也会受到一定程度的影响。为了评价这种影响,需要定义如下指标:
信噪比说明了去噪操作的性能,定义为式中:X(i)——原始的参考信号;
Y(i)——去噪信号;
N——采样点数。
正的SNR说明信号的能量大于噪声,反之,噪声的能量大于信号。
但是在实际处理中,原始参考信号往往很难得到,所以一般看噪声降低的程度:式中Z(i)为噪声加PD信号。
PD脉冲幅值的衰减比例:式中:X——PD信号峰值;
Y——去噪之后恢复信号的峰值。
在仿真中,由于模拟了PD脉冲信号,所以衰减比例得以计算。
另外,为了比较去噪信号和原始信号相比额外的失真,需要计算输入信号和去噪之后信号的相关系数,定义为式中X(i)为输入信号(1,…,N),表示去噪之后的信号(1,…,N)。相关系数的范围为-(N-1)~(N+1),表示两个信号的相似程度,也反映了去噪之后波形的失真情况。
总之,只有当SNR比较高,幅值的衰减比较少,并且波形的失真最小时,才能说该去噪方案有效。值得一提的是,这里面考虑了边界的影响和相位平移。
计算得本方案的SNR为50.2dB,相关系数为0.99,并且提升的SNR为99.86 dB。这样无论定性和定量都说明了本方案的有效性。
3现场验证
将传感器依次放置在GIS盘式绝缘子处或电缆接头处,观测是否有局部放电脉冲信号,并对其进行测量。模拟典型的沿面放电,并且在测试中加入人为的手机信号干扰。在放电类型识别中提取相位相关特征,这里以相位一放电量为例。统计了1s,也就是50个周期的放电信号,统计出相位一放电量二维图。图5是没有进行干扰消除的相位一放电量二维图,可以看出手机干扰信号和PD统计信号完全混合在一起。由于手机干扰信号能量比较强,噪声信噪比非常小,在这种情况下,虽然通过肉眼大致可以识别放电类型,但是对于在线系统,误差非常大,只有20.1%沿面放电的可能。经过去噪之后的结果如图6,可以看出手机干扰基本被消除,经模式识别之后,沿面放电的可能性比例达到了92.3%。
4结束语
本文利用小波变换对局放监测过程中干扰信号进行了时频分析,根据PD信号的特征,提取出有用的信号,并进行重构。该方案可以滤除大部分类型的干扰,这对放电类型的诊断具有很大帮助。采用Matlab仿真和现场试验分别验证了该算法的有效性。

