LDG方法基本思想

王建珍

（长治学院 数学系，山西 长治 046011）

LDG方法基本思想

王建珍

（长治学院 数学系，山西 长治 046011）

文章阐述了一维非线性双曲问题LDG方法的基本思想，给出单元熵不等式和L2-稳定性的证明，最后给出了基函数的具体求解步骤。

LDG方法；双曲方程；基函数；稳定性

1 引言

局部不连续伽辽金 （Local discontinuous Galerkin）方法，简称LDG方法，是一种间断有限元方法.

间断有限元方法最早可以追溯到1973年Reed和Hill关于中子输运方程的论文[1]，特别是80年代以来，出现了各种各样的间断有限元方法.近年来发展的间断Galerkin有限元方法[2][3][4]，特别是90年代以来，以Cockburn和Chi-Wang Shu为代表提出的Rung-Kutta DG方法[5]，特别引人注目，在许多应用上显示了前所未有的效能.

间断有限元方法既保持了有限元方法和FVM的优点，又克服了其不足，特别是易于处理复杂的边界和边值问题.同时DG方法具有灵活处理间断的能力，克服了一般有限元方法不适宜于间断问题的缺点.DG方法精度的提高可以通过适当选取基函数，即提高单元插值多项式的次数来实现.对于含有高阶空间导数的方程，DG方法不能被直接应用，这是因为解空间是由不连续的分段多项式组成.也就是说，近似解仅在时间上是间断的，在空间中却不是，空间离散是用连续有限元的标准DG方法.LDG方法却不同，它是用间断有限元方法进行空间离散[5]，因而LDG方法也是对DG方法的发展.

首先LDG方法是Cockburn和Shu应用于非定常对流-扩散方程中，后来这个方法又被成功地推广到一般地含有三阶导数的Kdv型方程及含有四阶和五阶导数的偏微分方程[5]中.

LDG方法的主要思想是将原来带有高阶导数非定常的偏微分方程引进辅助变量重写成一个一阶方程，然后通过RKDG方法进行离散.对于近似解的导数，引进这些局部辅助变量是表面的，在具体问题中很容易被消除.

LDG方法成功的关键因素是单元接触面处的数值流设计，所有数值流设计必须保证数值流的稳定性和局部相容性.

2 一般的一维非线性双曲问题LDG方法的基本思想：

最简单的DG方法被设计是为了去解决最简单的一次双曲问题.为说明思想，首先研究一般的一维非线性简单模型：

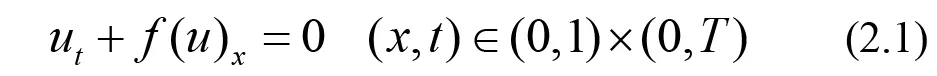
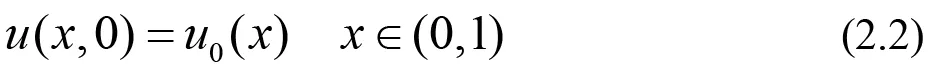
带有周期边界条件

我们进行空间离散,对于区间(0,1)任取分割

如果我们用任意光滑检验函数v(x)乘以 (2,1)和(2,2)，并在Ij上积分，进行简单的正常分部积分后得到：

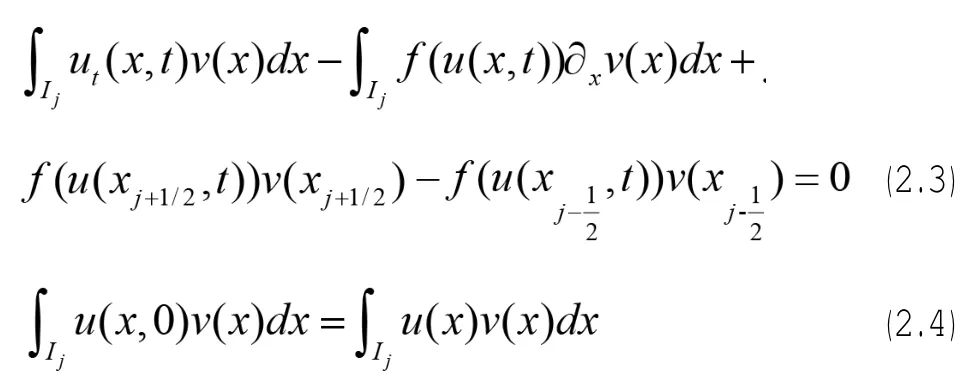
这正是DG方法的起点，接下来，设

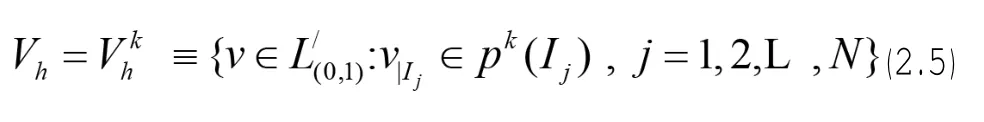
其中，Pk(I)表示I上最多K次多项式空间.我们用最多K次分段多项式uh和vh分别代替解u(x,t)和检验函数v(x,t)，即uh,vh∈Vh,当(2.3)中u和v被uh和vh代替时，式中的在点取值的最后两项中，近似解uh和检验函数vh在这些边界点处是间断的，将要用一种迎风结构处理这些项.所以在分界点处，uh采用迎风的单值数值流vh在处以IJ内部取值，即：

vh在处仍从Ij的内部取值分别为

若在(2.7)中取vh为常数，不妨取vh=1，(2.7)变为：

可以看出，当基函数取为常数时，DG方法可还原为有限体积方法，即一阶的DG方法相当于一阶的有限体积方法.

剩下的工作也仅是数值流h的选择.首先要求选择是稳定的，更重要地想要成为所谓的单调格式，从而达到高精度而保持稳定性和收敛性质.

我们从K=0情况入手，也就是uh是分段常数函数时，DG空间离散产生的一种单调格式.

并且要求(2.6)中的h(a,b)满足：

1o)它是局部满足Lipschitz连续，并且和f(u)相容，即h(u,u)=f(u)

2o)它对第一个变量是不增函数

3o)它对第二个变量是不减函数

这样的h(a,b)就定义为一个单调格式.常用的单调格式有：

⑴Godunov流：

⑵The Engquist-Osher流：

⑶The Lax-Friedrichs流：

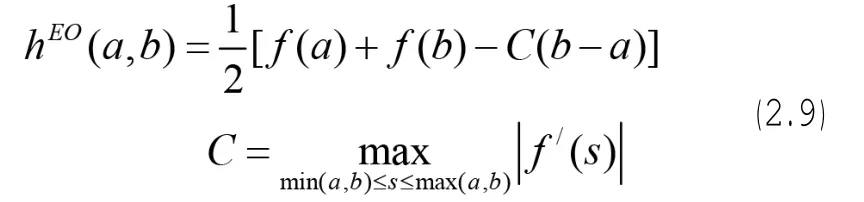
⑷The Local Lax_Friedrichs流：

⑸带有“熵固定”的Roe流：

我们能容易使用数值流hG.因为它是产生人工粘性最小的数值流.局部Lax-Friedrichs流比hG流产生更多人工粘性，但他们的性能非常相似.如果f很复杂时，通常用hLF流.然而，数值经验告诉我们，当逼近的多项式次数K增加时，数值流的选择不影响逼近的特性.

定理2.1（单元熵不等式）对于数值格式(2.7) -(2.9)，我们有熵不等式:

其中

证明：在(2.7)中取vh=uh有

则上式可化为:

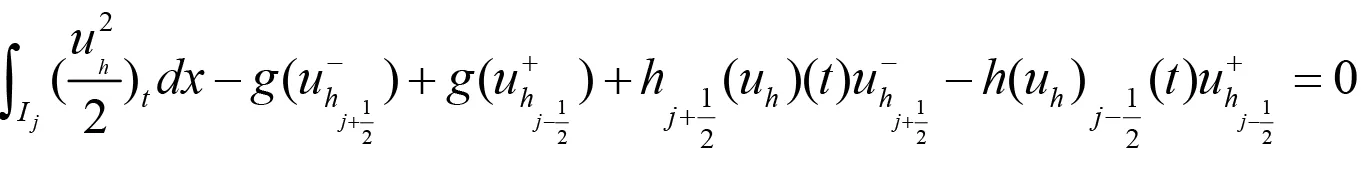
由于

定义

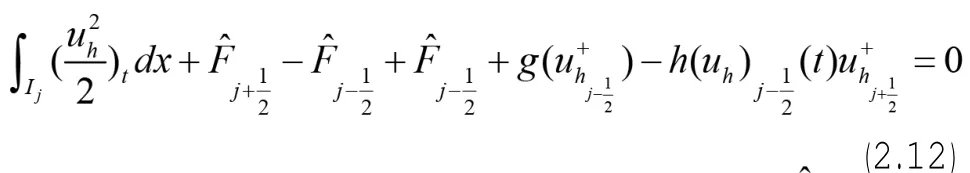
i)如果利用h(a,b)单调性f(↑,↓)，可知

再回到(2.12)就可以得到熵不等式：

将上式中j=1,2,…N相加，易得L2稳定性.

定理2.2 (L2-稳定性)对于格式(2.7)-(2.9)有,即∀T＞0有

3 基函数及具体求解步骤：

由于Vh中的函数可以出现间断，不同单元上的基函数可以相互无关，因此需要在每个小IJ上取局部基函数.如果我们选择Legendre多项式PJ作为局部基函数，可以利用他们的L2正交性，即：

和性质Pl(1)=1,Pl(-1)=(-1)1,进行讨论.

令φl(x)=Pl(2(x-xj)/Δj) x∈Ij近似解uh可以表示为

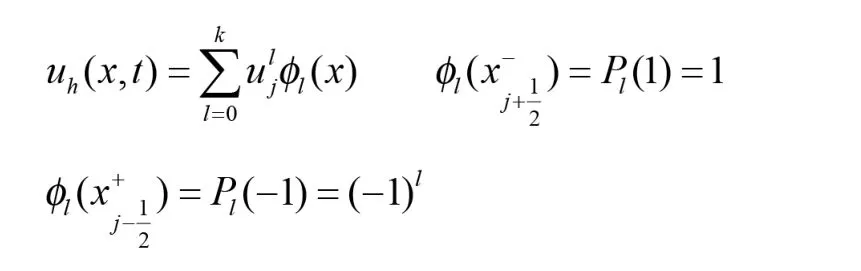
对于弱形式(2.7)和(2.8)，取vh(x)=φl(x);可得下列简单形式：

∀j=1,2,L,N和l=0,L,K

进一步可化为：

是简单的对角矩阵.

从而，可以给出这种间断有限元方法的具体计算步骤：

(3)计算

注意：如果我们选择不同的局部基函数，所形成的质量矩阵能为一个全矩阵，但它永远是k+1阶方阵[6].

以上是对LDG方法的思想、稳定性、线性情况的误差估计和离散方法进行了分析和讨论，对于多维情况可以使用相应的手段进行.

［1］Reed w H and Hill T R.Trangular mesh methods for the Newtron transport equation.［M］LA Report,1973.

［2］Erirsson K,Johnson C and Thomenn V.Time discretization of parabolic problem by the discontinuous Galerkin method.RAIRO.［J］Anal Unmer 1985,（19）:912-928.

［3］Hulme B L.One-step piecewise polynormial Galerkin methods for initial value problems.Math comp,1972,（26）:415-426.

［4］Jamet P.calerkin-type approximation which are discontinuous in time for parabolic equation in a variable domain.［J］SLAM J Numer Anal,1978,（46）:1-26.

［5］CockburnB,HouSandshuC W.TVB Runge-kutta local projection discontinuous Galerkin finite eiement method for scalar conservation laws IV;The multidimensional case.［J］Math comp,1990,（54）:545-581.

［6］刘儒勋，舒其望著.计算流体力学的若干新方法.［M］.北京：科学出版社，2004.160-161.

（责任编辑 赵巨涛）

O241.8

A

1673-2015（2015）02-0004-04

2014—11—23

王建珍（1962—）女，山西太原人，副教授，主要从事高等数学教学与研究。