石灰处理软土路基深度与土基当量回弹模量关系研究
马士宾,孙敬福,袁文瑞,陈奕
(河北工业大学土木工程学院,天津 300401)
石灰处理软土路基深度与土基当量回弹模量关系研究
马士宾,孙敬福,袁文瑞,陈奕
(河北工业大学土木工程学院,天津 300401)
在室内外试验基础上,针对现行规范换算方法不适用于低模量比石灰土路基情况,根据弹性层状体系理论以及弯沉等效原则,采用KENPAVE和Minitab软件回归出了精度和可靠性较高的换算公式.并通过此公式分析了石灰处理软土路基深度与土基当量回弹模量间的关系.分析结果表明,随石灰处理深度的增加,路基顶当量回弹模量值也在增大,而且增大幅度明显;在达到相同当量回弹模量设计目标时,粘性土的处理深度要大于砂性土的处理深度,而且处理深度相差也非常明显.最后通过实例说明本文当量回弹模量换算公式可用来代替规范中换算公式计算低模量比当量回弹模量值.为软土路基设计与施工提供指导.
粘性土;砂性土;路基;模量;含水量;压实度
目前,利用石灰处理软土路基以提高土基回弹模量是工程中经常采用的技术措施[1],同时也取得了不错的效果.但是,由于软土含水量、土质特性、石灰掺量、石灰处理路基深度等因素对土基回弹模量都有很大影响[2-3],到目前为止,还没有关于石灰处理软土路基深度与土基回弹模量之间关系的研究,造成在实际工程中石灰处理软土路基盲目性和随意性很大.比如在设计施工时,不考虑原状软土路基回弹模量与设计目标值的大小,就按经验随便选择一个处理深度来改良软土,结果造成处理深度过小路基顶回弹模量达不到要求,路面结构容易损坏;处理深度过大时,又造成经济上的浪费.
因此,针对具体的路基特征,研究石灰处理软土路基深度和土基回弹模量之间的关系,确定合理的石灰处理土基深度值来指导设计和施工就显得尤为重要[4].为此,本文以天津软土地基为例,通过室内外试验,深入研究石灰处理软土路基深度对土基回弹模量的影响,这对于完善设计规范、确保道路工程质量和节约工程建设成本都具有十分重要的现实意义.
1 试验分析
1.1 原材料分析
本文试验所用土样和石灰均取自天津市河北区与北辰区的两处城市道路施工现场.消石灰按《公路工程无机结合料稳定材料试验规程》(JTG E51-2009)中T0813-1994的规定进行检查[5],其等级为Ⅱ级钙质消石灰,部分指标见表1.土样的取土深度为0.3~1m,土质分为2种:河北区土样为粘性土,对其分别进行了基本物理力学性质试验,结果如表2和表3所示.
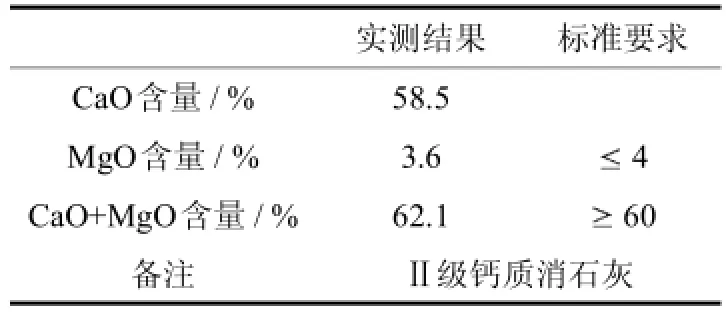
表1 石灰技术指标Tab.1Lime technical index

表2 粘性土物理力学性质Tab.2The physical and mechanical properties of cohesive soil

表3 砂性土物理力学性质Tab.3The physical and mechanical properties of sand soil
1.2 试验方案及过程
软土天然含水量均较大,施工时很难将含水量控制到最佳含水量附近[6].因此,为符合实际,本试验选则2个含水量,分别为20%和25%,高于其最佳含水量,并在此基础上分别加入8%、10%、12%的石灰,同时按90%、93%和96%来控制压实度进行试验.
试验过程严格按照《公路工程无机结合料稳定材料试验规程》(JTG E51-2009),对石灰土最大干密度、最佳含水量、抗压回弹模量方面进行试验.
1.3 试验结果分析
石灰能显著提高软土的抗压回弹模量.素粘性土试样7 d抗压回弹模量为14.3~18.5 MPa,粘性土石灰稳定土试样的7 d抗压回弹模量为36.2~95.4 MPa;砂性土素土试样的7 d抗压回弹模量为15.7~20.3 MPa,砂性土石灰稳定土试样的7 d抗压回弹模量为41.9~100.2 MPa.石灰土模量仍比较低,大概在30~100 MPa之间.
2 路基当量回弹模量换算方法分析
2.1 现行规范换算方法存在的问题
现行的当量回弹模量换算方法,是按双层弹性体系理论解的回归公式确定均质体的当量回弹模量[7-8],换算公式如下

2.2 基于石灰处理软土路基的当量回弹模量换算公式回归分析
这里运用KENPAVE软件计算弯沉值.在计算过程中,圆形均布荷载作用直径为30 cm,接地压强为700 kPa,双层结构计算参数如图1所示.
选取图1中的路面结构参数,计算出不同处理厚度和不同模量下的表面弯沉值,然后采用弹性层状体系理论,按弯沉等效原则计算出各种结构参数下路基顶部当量回弹模量Et,计算结果如表4所示.

其中:l0和lt分别是均质半无限空间体模量E0和Et对所对应的弯沉值.
应用Minitab统计分析软件对各种结构组合下的一系列数据进行回归分析,从而得到相应的因变量与自变量之间的换算回归公式.
参考规范中计算公式的形式,假设

则根据层状体系地基的计算结果进行回归分析可以得到
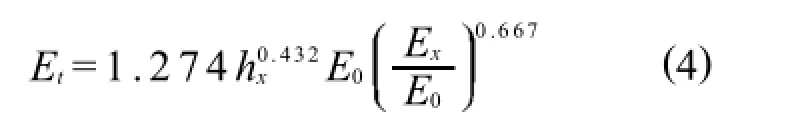
式(3)和式(4)中:Ex为石灰稳定土回弹模量,MPa;hx为石灰稳定土厚度,m;E0为土基回弹模量,MPa;Et为路基顶当量回弹模量,MPa.
该回归公式的R2=0.976,说明该公式回归相关性非常好.
本文为验证拟合公式(4)的精度与可靠性,选取了图1中双层结构计算参数进行分析,并分别与规范解和弹性层状体系理论解进行了比较.本文拟合公式相比于规范公式(1),其计算结果更接近于弹性层状理论解,误差相对减小很多.这说明将双层结构按等效弯沉原则转化为当量单层结构来确定软土路基均质体的当量回弹模量是可行的.

图1 双层结构计算参数Fig.1Structure calculation parameters
3 石灰处理软土路基深度与土基回弹模量关系分析
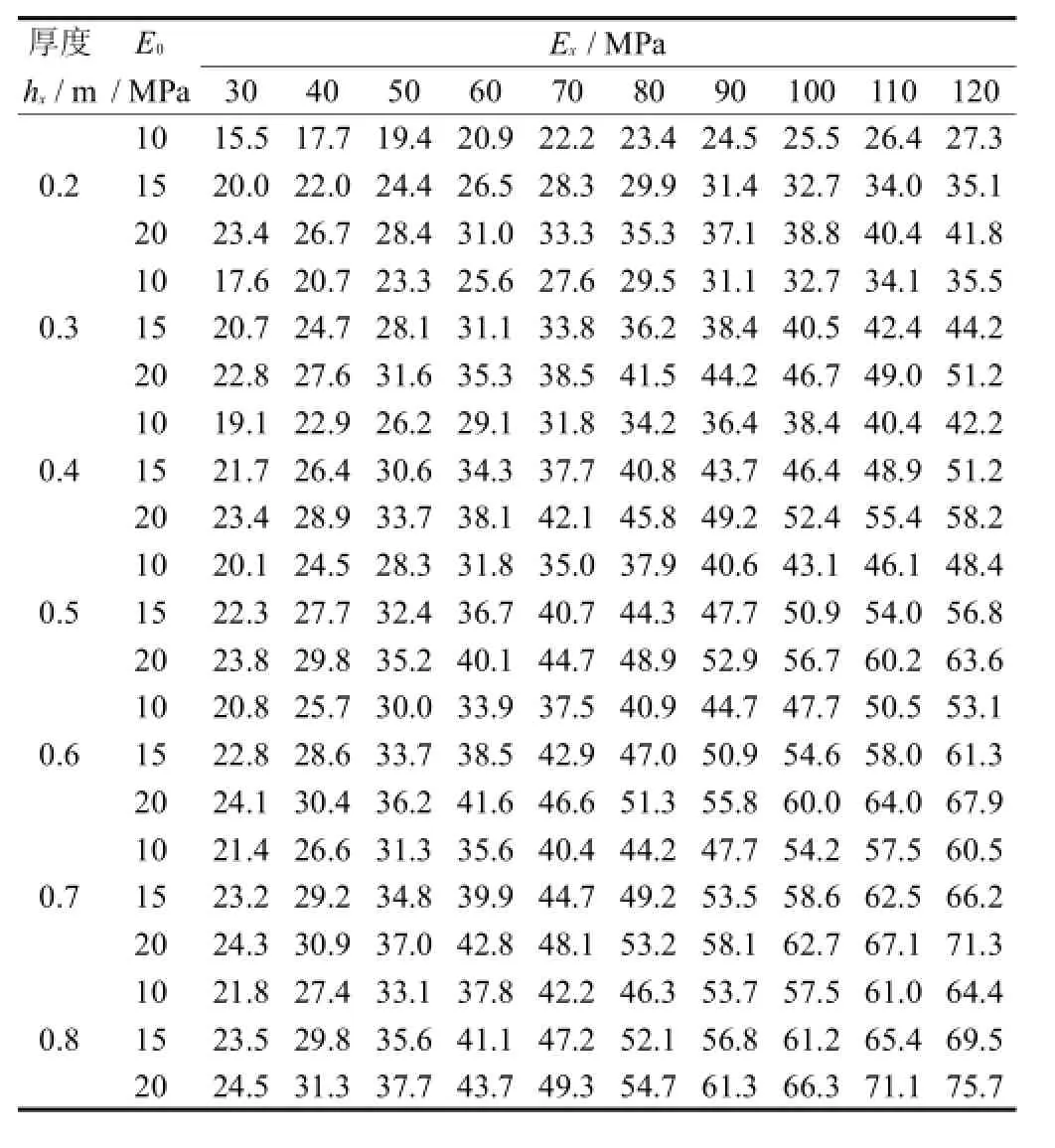
表4 路基顶当量回弹模量Et计算结果Tab.4Calculation results of the soil base equivalent resilience modulus
3.1 石灰处理软土路基深度对土基回弹模量影响分析
根据试验结果,通过拟合得到的路基顶当量回弹模量计算公式(4),可以分别计算出粘性土和砂性土在不同处理深度时的路基顶当量回弹模量值,其不同处理深度下回弹模量值比较如下图2至5所示(图中T表示石灰含量,K表示压实度).

图2 粘性土20%含水量不同处理深度下回弹模量值比较Fig.2Comparing processing depth with rebound modulus of cohesive soil of 20%water content

图3 粘性土25%含水量不同处理深度下回弹模量值比较Fig.3Comparing processing depth with rebound modulus of cohesive soil of 25%water content

图4 砂性土20%含水量不同处理深度下回弹模量值比较Fig.4Comparing processing depth with rebound modulus of sandy soil of 20%water content
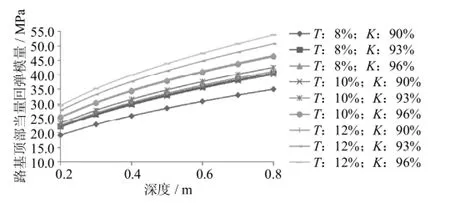
图5 砂性土25%含水量不同处理深度下回弹模量值比较Fig.5Comparing processing depth with rebound modulus of sandy soil of 25%water content
由图2~图5可知,随石灰处理深度的增加,路基顶当量回弹模量值也在增大,而且增大幅度明显,从0.2m加大到0.8m,当量回弹模量值可以增大一倍左右;随石灰剂量或者压实度增大,路基顶当量回弹模量值也在增大.对比相同含水量、石灰含量及压实度情况下,处理相同深度,砂性石灰土路基顶当量回弹模量值要大于粘性石灰土,其原因就是在同一含水量、石灰含量和压实度情况下,砂性土试样回弹模量值要比粘性土大.
3.2 土质特性对石灰处理软土深度的影响分析
根据回归得到的当量回弹模量计算公式(4),可推导出石灰处理软土深度与目标回弹模量值之间关系式

式中:hx为石灰稳定土厚度,m;Et为路基顶当量回弹模量目标值,MPa;E0为土基回弹模量,MPa;Ex为石灰稳定土回弹模量,MPa.
现行《城市道路路基设计规范》(CJJ194-2013)规定,快速路和主干路路基回弹模量值应大于30MPa,次干路和支路路基回弹模量值应大于20 MPa.因此,本文选择30 MPa和20 MPa分别作为快速路和主干路及次干路和支路的路基顶当量回弹模量设计目标值,计算石灰处理软土深度,并对比分析不同土质对石灰处理深度的影响.表5~表8为粘性土和砂性土在不同含水量下达到回弹模量设计值的石灰土处理深度(表中T表示石灰含量,K表示压实度).

表5 粘性土20%含水量下石灰处理深度Tab.5The lime treatment depth under 20% water content of cohesive soil
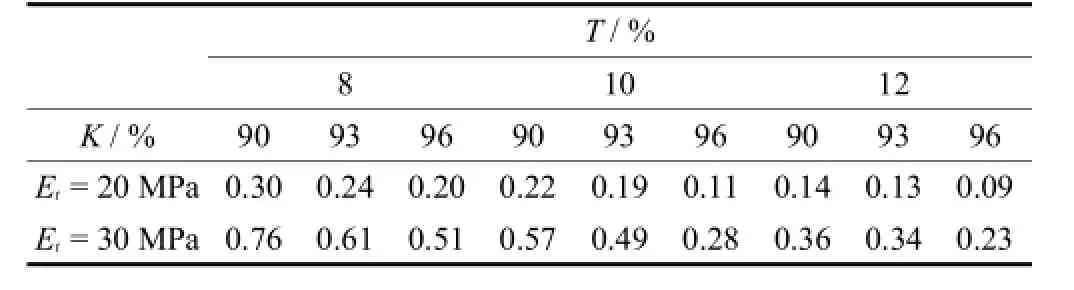
表6 粘性土25%含水量下石灰处理深度Tab.6The lime treatment depth under 25% water content of cohesive soil
由表5~表6可以看出,粘性土20%含水量时,达到20 MPa设计值需要的处理深度在0.05~0.19 m之间,达到30 MPa设计值需要处理0.14~0.47 m;25%含水量时,达到20 MPa设计值需要的处理深度在0.09~0.30 m之间,达到30 MPa设计值需要处理0.23~0.76 m,说明石灰含量和压实度对粘性土处理深度的影响非常大.对不同的回弹模量设计值,虽然只增大了10 MPa,但是处理深度基本上都要增大一倍以上.
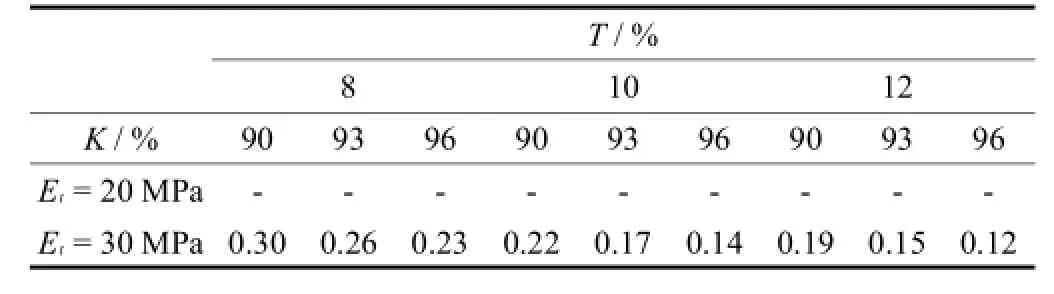
表7 砂性土20%含水量石灰处理深度Tab.7The lime treatment depth under 20%water content of sandy soil

表8 砂性土25%含水量下石灰处理深度Tab.8The lime treatment depth under 25%water content of sandy soil
由表7~表8可知,砂性土20%含水量时,其本身的抗压回弹模量已达到20.3 MPa,以此不需要掺加石灰加固,达到30 MPa设计值需要的处理深度在0.12~0.3 m之间;25%含水量时,达到20 MPa设计值需要的处理深度在0.08~0.22 m之间,达到30 MPa设计值需要处理0.21~0.56 m.说明石灰含量和压实度对砂性土处理深度的影响也非常大.对不同的回弹模量设计值,虽然也只增大了10 MPa,但是处理深度同样都要增大一倍左右.
此外,对比分析粘性土和砂性土两种土质在相同的含水量、石灰含量和压实度情况下,达到相同的当量回弹模量设计目标值所需的石灰处理深度.可以看出,不管是达到20MPa还是30MPa,粘性土的处理深度都大于砂性土的处理深度,而且处理深度相差也非常明显.根据试验结果可知,其主要是砂性土经同样处理后,强度增长幅度要大于粘性土.
4 实例验证
为对比理论计算得到的路基顶当量回弹模量与实际工程中实测路基顶当量回弹模量值,本文结合天津市北辰区某道路工程的施工进度,在其处理路基土层时对路槽顶面和每层石灰土顶面的弯沉进行了检测.通过室外试验,测得原状软土路基的回弹模量为10.1 MPa.根据检测结果以及弯沉等效原则(公式2),可以反算得到每层石灰土顶面的回弹模量值.
室内试验测得该软土在10%石灰含量、96%压实度时的回弹模量值为58 MPa,再结合本文回归得到的换算公式(4),可计算得出每层石灰土顶面的当量回弹模量值,见表9.
由表9可以看出,本文回归得到的公式所计算的当量回弹模量值与经弯沉检测反算得到的回弹模量值非常接近,误差很小.说明本文的当量回弹模量换算公式具有很好的精度与可靠性,可以用来代替规范中的公式来计算低模量比的当量回弹模量值.
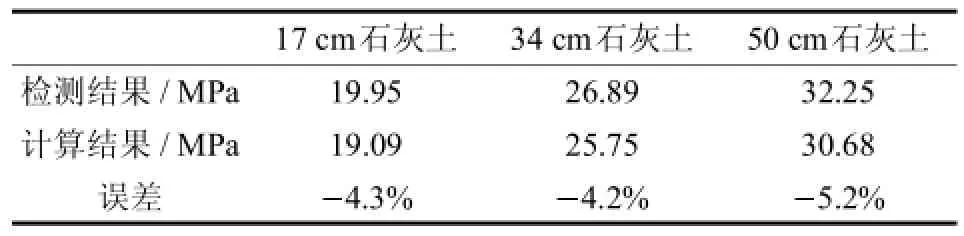
表9 回弹模量计算结果与检测结果对比Tab.9Comparison of calculated results with the test results of resilience modulus
5 总结
1)针对当前规范中当量回弹模量换算公式不适用于低模量比的石灰土路基情况,本文按弹性层状体系理论及弯沉等效原则,通过KENPAVE和Minitab软件,回归出一个荷载作用半径为15cm的换算公式.回归出的新公式适用于石灰土与原状软土模量比小于8且石灰处理厚度大于20cm的精度与可靠性均较高的路基顶当量回弹模量换算.最后通过施工现场实测弯沉与模量验证了回归公式.
2)随石灰处理深度的增加,路基顶当量回弹模量值也在增大,且增大幅度明显,从0.2 m加大到0.8m,当量回弹模量值可以增大一倍左右;随石灰剂量或者压实度增大,路基顶当量回弹模量值也在增大.对比相同含水量、石灰含量和压实度情况下,处理相同深度,砂性土的路基顶当量回弹模量值要大于粘性土.其主要就是在同一含水量、石灰含量和压实度情况下,砂性土试样的回弹模量值比粘性土大.
3)粘性土和砂性土两种土质在相同的含水量、石灰含量和压实度情况下,达到相同当量回弹模量设计目标值,不管是20MPa还是30MPa,粘性土的处理深度都大于砂性土的处理深度,而且处理深度相差也非常明显.主要就是砂性土经同样处理后,强度增长幅度大于粘性土.
[1]黎卿.石灰在软土路基中的应用及施工方法[J].公路交通科技(应用技术版),2014(7):127-129.
[2]KhanBazid,SirajAbdus,KhattakRiazA.Pavementsubgradeimprovement bylime[C]//AdvancedMaterials Research(Vol587),2012:93-96.
[3]谢雪.天津滨海新区软土路基处理方案研究[D].天津:河北工业大学,2010.
[4]袁文瑞,李笑笑.石灰处理软土路基当量回弹模量换算新方法[J].交通标准化,2014(2):83-86.
[5]中华人民共和国交通部.JTG_E51-2009,公路工程无机结合料稳定材料试验规程[S].北京:人民交通出版社,2009.
[6]张平芳.公路工程软土路基处理技术分析[J].交通标准化,2012(14):112-114.
[7]王振辉,蔡良才,顾强康,等.基层顶面当量回弹模量确定方法的修正[J].空军工程大学学报,2009,10(6):23-27.
[8]邱欣,杨青,钱劲松.水网密集区粘土路基当量回弹模量的预估分析[J].土木建筑与环境工程,2011(2):38-44.
[责任编辑 杨屹]
The relation between the depth of lime treating soft soil subgrade and the soil base equivalent resilience modulus
MA Shibin,SUN Jingfu,YUAN Wenrui,CHEN Yi
(School of Civil Engineering,Hebei University of Technology,Tianjin 300401,China)
Faced with the current criterion conversion method is notsuitable for low modulus ratio and based on the indoor and field tests,this paper uses KENPAVE and Minitab software to regress accurate and reliable conversion formula according to the elastic multi-layer theory and principles of displacement equivalence.Then the relation between the depth of lime treating soft soil and the soil base equivalent resilience modulus are analyzed.Analysis showed that the soil base equivalent resilience modulus values can increase significantly with the increase of lime treated subgrade depth.When reaching the same soil base equivalent resilience modulus design value,the processing depth of cohesive soil was higher than the processing depth of sand soil,and processing depth difference was also very obvious.Finally,this paper uses a practical example to illustrate that the equivalent resilience modulus conversion formula can be used to replace the current criterion conversion formula to calculate lime treating soft soil subgrade equivalent resilience modulus of low modulus ratio.This research can provide reference for design and construction of soft soil subgrade.
cohesive soil;sandy soil;subgrade;resilience modulus;water content;compactness
U416.1
A
1007-2373(2015)05-0097-05
10.14081/j.cnki.hgdxb.2015.05.020
2015-04-10
河北省高等学校科学技术研究项目(ZD2014099)
马士宾(1973-),男(汉族),副教授,博士.

