基于运行时间预测的枢纽内多线路协调调度研究

于 滨， 崔 瑶， 蔡婉君， 马 宁

(大连海事大学 交通运输管理学院，辽宁 大连 116026)



基于运行时间预测的枢纽内多线路协调调度研究

于 滨， 崔 瑶， 蔡婉君， 马 宁

(大连海事大学 交通运输管理学院，辽宁 大连 116026)

针对传统调度模型预见性不强的弱点，提出一个基于支持向量机(SVM)的公交车辆到达枢纽时间的预测模型，基于该模型构建以所有乘客节约时间最大为目标的调度模型，动态协调公交车辆从枢纽的发车时间，并基于遗传算法对该模型进行求解。最后，我们以大连市沙河口火车站枢纽为实例，对该模型和算法的可行性进行了检验，结果显示，本文提出的调度方法优于传统调度策略。

交通运输规划与管理；公交动态车辆调度；到达时间预测；SVM模型；遗传算法

0 引言

在换乘枢纽内进行公交车辆动态调度可以最大化地实现不同线路上的车辆的同步到达，进而显著地减少乘客换乘时间，提升公交服务水平。由于实际生活中公交车辆的运营环境十分复杂，存在很多随机干扰因素(如天气变化，交通拥堵以及客流的变化等)，保证静态调度的最优结果十分困难。因此，针对意外情况做出快速且有效地动态调度研究十分重要。另外，实施公交动态调度的一个重要前提就是能够及时、准确地对公交线路上车辆未来的分布状态进行预测，其预测的精度直接关系到调度方案选择的准确性。

在动态调整策略中，滞站调度被广泛应用于公共交通运输领域，因此本文重点研究了滞站策略。Lin指出滞站策略是指公交车辆在站点适当延长发车时间的调度方法，包括基于行车间隔的滞站策略和基于时刻表的滞站策略[1]。Ting 和Schonfeld基于乘客的时间成本，提出了在换乘枢纽进行公交滞站的策略，并采用启发式算法来最优化乘客的等待时间，且用具体数例探讨了不同情况下乘客等待时间的变化情况[2]。Lam提出了一种基于集成仿真模型和服务可靠性评价方法的多响应优化方法来优化公交调度策略，其中，仿真模型是由载客量预测和发车间隔频率波动组成的双马尔科夫模型。最后，他们采用新加坡的实例验证了其提出的方法的可行性[3]。Chowdhury以基于乘客总换乘时间最少为目标，提出了在换乘枢纽进行公交调度的车辆动态调度方法，此外，他们还开发了计算车辆调度时间的算法[4,5]。Dessouky提出了一种公交车辆到站时间预测的方法，并且通过仿真方法对该方法进行检测，结果发现当发车延误很小，行车间隔较大和联通线路较多时，公交到站时间预测的结果准确度很高。此外，他们发现依靠通讯、跟踪和乘客计数的技术手段获取的信息能为公交滞站调度提供更为有效的技术支持[6]。此外，还有一些学者进行了关于公交运营时刻表同步性的研究，如文献[7～9]。本文首先采用支持向量机(SVM)模型挖掘公交运营历史信息的潜在规律，进而预测公交车辆到达枢纽的时间，并以乘客总节约等待时间最多为目标，对枢纽内公交车辆的派遣计划进行了优化。

1 公交车辆运行状态预测方法

公交车辆运行时间预测是进行动态调度的基础，公交运营企业根据车辆运行的特点及实时信息来确定是否需要调度以及调度时间的长短等。由于在对枢纽点的公交车辆进行调度时，需要考虑到来自不同线路换乘的影响，因此，获得其他公交线路上的车辆预计到达换枢纽点的时间对枢纽点公交车辆的最优调度策略十分重要，但在实际中，很多随机因素会干扰公交车的运行，提供准确的公交到达枢纽点的时间预测模型是一项非常具有挑战性的工作。

国外很多学者已经采用神经网络模型或支持向量机模型进行了公交到达时间的等预测，如文献[10～17]。然而，很多研究表明神经网络模型往往难以训练，甚至不稳定，很难得到全局解或唯一解。Vapnik指出SVM模型是一种基于统计学习理论的机器学习方法，能很好的抵制过拟合问题，同时满足对泛化性的要求。近来，SVM模型已成功地应用于交通运输领域，如事件监测、交通模型的识别、行程时间预测等[18,19]。本文采用SVM模型来对两辆连续到达车辆的时间间隔进行预测。如果将枢纽点视为某条线路的一个站点，则基于枢纽点的车辆到达时间预测就可转化为基于单条线路的车辆到达时间预测。因此，本文将详细介绍基于枢纽点的下一车辆到达时间的预测方法。

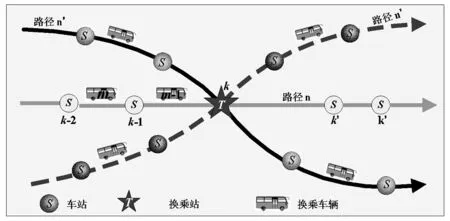
图1 基于枢纽的车辆运行状态图

预测下一辆公交到站时间的基础是当前车辆和下一车辆的到达换乘站的时间间隔，因此根据当前车辆的到达换乘站的时间以及对下一车辆到站时间间隔的预测，就可以计算出下一车辆到达换乘站点的时间。如图1所示，假设有三条线路和一个换乘站点，当线路n上通行的公交车m-1到达换乘站点k时，根据目前的观测数据，可预测出前车m-1(“前车”和“后车”是相对而言的，先到达枢纽的被称为“前车”)和下一辆车m的到站时间间隔。

由于随机干扰因素的存在及不同运行环境的影响，连续车辆到站的时间间隔在运行中是不断变动的。其中，道路交通状况被普遍认为是影响车辆运行的最重要因素之一，且在早晚高峰期间其影响尤其明显。本文采用SVM构建换乘站点下一车辆的到达时间间隔预测模型，采用两类输入变量：最新车辆与上一辆车到站时间间隔和换乘站点周围几条线路上的当前交通状况。同时，为了更加准确地反映出车辆运行情况，当某一车辆到达站点时，对其与之前的车辆到站的时间间隔进行更新。某站点当前车辆的到达时间减去上一辆车到站时间可以得到最新到站时间间隔。

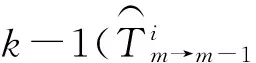
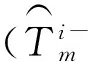
图2 基于SVM的公交车辆运行时间预测模型

2 换乘枢纽调度优化模型

换乘枢纽点的公交动态调度不但与换乘站乘客的等待时间相关，而且还与下游站乘客的等待时间有关。本文所研究的城市公交枢纽站动态调度策略是基于调度策略实施前后总的等待时间差最大化为目标，即通过分析等待时间来决定哪辆车在换乘站点是按照时刻表发车，还是对其进行调度，以等待与其相连的线路上车辆的到达。如果对某车辆进行调度，首先需要计算不进行调度时车辆的发车时间，然后，根据预计正常发车时间后的换乘乘客的等待时间减少，以及由于调度引起的非换乘乘客、下游站点乘客的等待时间的增加来确定车辆的最佳调度时间[20]。下面对动态调度策略主要影响因素进行分析：

模型中所用的字母含义如下：

u、d—上车、下车;A、D—公交到达、离开站点;N—乘客数量;n,n′—公交线路;Δ,Δ′—公交行驶方向;-, + —调度前或调度后的情况;r—乘客到站率，即单位时间内到达的乘客数;h—调度过程中的情况;s—公交车停靠时的情况;^—预测符号;t—换乘;a—非换乘乘客到达站点;w—步行。

在无特殊说明时，所用符号均代表换乘站点k的情况。

2.1 车辆m不进行调度的预计离站时间

如果不将车辆调度产生的影响考虑在内，与车辆m的发车时间的相关因素为：非换乘乘客、在车辆m到达换乘站点前与其相连的线路上换乘乘客的上下车时间。

(1)

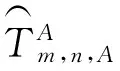
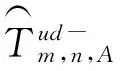
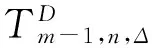
λn,Δ—假设乘客服从均匀分布的情况下，第n条线路上Δ方向上乘坐车辆m的非换乘乘客到站率。

Step 2 计算从线路n′上Δ′方向上的车辆i下车的乘客且准备换乘线路n上Δ方向上车辆m的乘客数，假设这些乘客先于车辆m到达换乘站。

(2)

式中，vi,n′,Δ′—线路n′上Δ′方向上车辆i在到达换乘站点时车上的乘客数；

Pi,n′,Δ′—线路n′上Δ′方向车辆i在换乘站点下车乘客的比例；

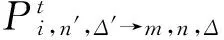
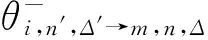
(3)

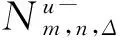
(4)

Step 4 估算线路n上Δ方向的车辆m在换乘站点的预计停靠时间，假设所有乘客在前门上车，后门下车。

(5)

(6)

2.2 车辆m调度期间预计上车乘客量

(7)

同理，在车辆m调度期间，从线路n′上Δ′方向的车辆i下来的乘客准备换乘线路n上Δ方向的车辆m的乘客数按下式计算：

(8)

(9)

则调度时期里乘坐车m的乘客数计算如下：

(10)

2.3 城市公交枢纽动态调度优化模型

本文假设车容量不限，换乘乘客与非换乘乘客的到达规律服从均匀分布，且只在枢纽点k对车辆m进行调度，则进行调度后，

(1)由于车辆m在换乘站点停靠时间延长，在站点k上车的部分乘客能够赶上车辆m，而无需等待车辆m+1，这部分人所节约的时间R1可按下式计算：

(11)

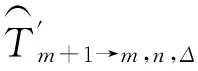
(2)由于车辆m到达下游站点k′的时间延长，在下游站点k′上车的部分乘客能够赶上车m，而无需等待m+1，这部分人所节约的时间R2可按下式计算：

(12)

式中，rk′,n,Δ—线路n上方向Δ下游站点乘客到达率

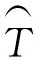
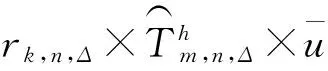
(13)

(3)由于车m在换乘站点调度使车m上原有乘客增加的等待时间C1：

(14)

式中，Nk-1→k,m,n,Δ—车辆m到达换乘站点k前的车内乘客数量

⑷ 由于车m在换乘站点调度引起的下游站点k'未能赶上车m-1且必须等待车m的乘客所增加的等待时间C2：

(15)

由于本动态调度优化模型是以在枢纽点对车辆m进行调度后所减少的等待时间最大为目标，因此，建立线路n上Δ方向的车辆m在换乘站点的动态调度优化模型，如下：

(16)

3 应用遗传算法求解动态调度问题

由于车辆在枢纽的发车时间直接影响到达枢纽的乘客数量，也间接影响后续站点的乘客等待时间，而另一方面，枢纽及后续站点的乘客数量又会影响调度计划的确定。因此，传统的解析算法很难对这类复杂问题进行求解，为了获得可接受的可行解，通常采用启发式算法来进行求解[21～23]，本文采用常用的启发式算法，即遗传算法对其进行了求解，具体求解步骤如下：

Step 1 编码策略。本文中，车辆在枢纽点的滞留时间是决策变量，而每辆车都有在枢纽点被滞留的可能，因此在编码时，枢纽点的所有车辆的滞留时间必须包含在内 (如果车辆不需要在枢纽点被滞留，则设其调度时间为0)。因此，本文采用了一个新型的十进制的编码，如下式所示。

(17)

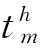
Step 2 选择操作。本文采用轮盘赌的方法从群体中选择出较适宜的用来繁殖下一代的父染色体。为了确保最好的基因能继续保存到下一代，避免遗传算法性能的退化，本文在选择父染色体的同时采用了精英策略，自动将适应值最高的染色体复制到下一代。

Step 3 遗传操作。本文采用了简单的单点交叉和简单变异方法。

Step 4 收敛判断。如果遗传操作得到的结果满足收敛条件或达到最大迭代次数或达到预选设置的个数时，则退出，否则转到选择操作继续搜索[24]。

4 实例研究

4.1 到达时间预测精度

本文选择大连市沙河口火车站作为测试环境，此枢纽衔接6条公交线路。详细的换乘站点和线路如图3和表1所示。为了获得准确车辆出行时间等数据，本文对2012年3～4月工作日的高峰期间此6条线路的所有公交车辆进行了调研，并得到了2万多组的有效数据。本文的SVM的输入参数为车辆在对应路段上的运行速度，因此，需要将收集到的车辆运行时间数据转化为其对应路段上的运行速度，然后，对所得到的数据进行归一化处理。根据SVM模型的特点，将数据分成以训练、交叉验证和检验为目的三个数据集。其中，作为检验的数据占样本量的10%，而将剩下的数据随机分成两组用来训练和交叉检验。本文根据以上搜集的数据进行了该研究路网的公交动态调度优化。

表1 换乘站点的线路信息

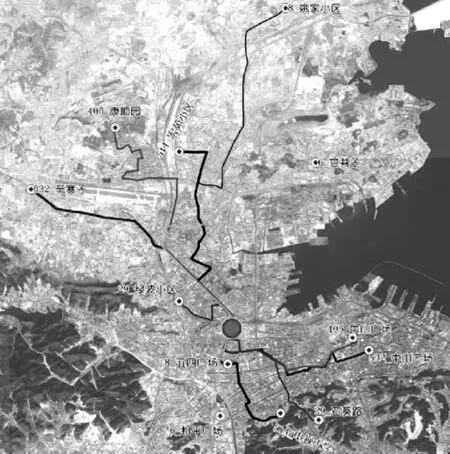
图3 换乘枢纽站及其服务的线路结构图

本文使用SVM来预测公交到达时间，运用径向基函数，由网格搜索得出SVM中的三个参数(C,εandγ)，并将其分别选定为(2-3, 2-5, 1.77)。

在SVM的模型中，由于速度很难直接测量，因此采用路段的长度和行驶的时间计算出的大致速度来替代公交行驶的实际速度，选取的预测精度为每次预测的平均绝对预测误差(MAPE)。MAPE可以表示为：

(18)

其中J为测试样本的数量。

为了检验本文提出的SVM模型的预测效果，本文对基于时刻表的模型(Schedule)、历史数据均值模型(HMP)和SVM采用相同的训练对测试数据进行测试，并对它们的结果进行比较。

在HMP模型中，首先对历史数据中公交车辆的平均速度进行计算，然后计算当前车辆到达换乘站点的时间。即：历史平均模型可以表示为：

(19)

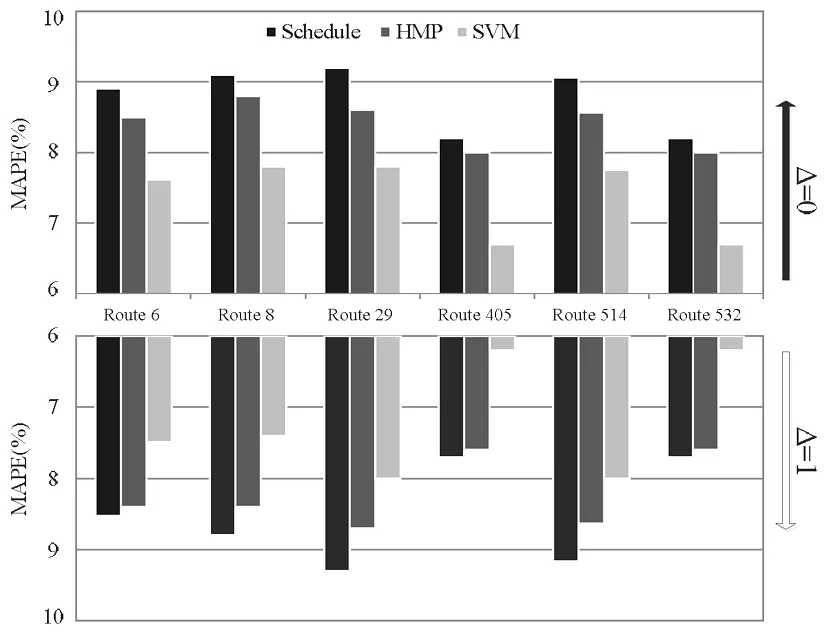
图4 预测性能比较

计算结果表明，Schedule，HMP和SVM三种模型的平均预测误差分别为8.53%，8.22%和7.21%。其中，对于每条线路而言，SVM模型的预测的误差都是最小的。三种模型的预测结果详细比较如图4所示。由于计划的行车间隔是基于一些静态的假设，实际中，一条线路上相邻车辆间不可能存在固定的时间间隔，所以基于时刻表模型的误差比SVM模型的大。与基于时刻表模型预测的结果相比，HMP可以提高预测精度，但其只是基于历史数据的简单统计模型，在此模型里，只包含车辆所在路段的交通状况以及之前的车辆信息，所以历史数据均值预测模型的误差均方根比SVM模型的要大。所以采用HMP不能获得一个比较满意的预测结果。通过比较这三个模型的预测结果，可以发现，基于SVM的模型能够根据枢纽点处相邻车辆时间间隔来达到好的预测结果。

进一步分析结果发现，在基于SVM的模型预测中，线路405和线路532的平均绝对预测误差(6.2%)要比其他线路的小，这是因为基于SVM的模型在预测到达时间间隔时将车辆的速度作为估算当前路段的交通状况，而线路405以及532的设计行车间隔较小，行车速度能够有效地反映交通状况随时间改变的特性。但是，可以看到，尽管线路8的行车间隔大，但其正向到达时间间隔预测的平均绝对预测误差(7.3%)也较小，这主要是因为线路8的正向车辆在到达换乘站点之前是在专用车道上行驶，车辆运行速度受早晚高峰拥挤因素的影响较小。

4.2 动态调度优化模型实例

为了对文中提出的动态车辆调度策略的结果进行检验，本文还讨论了一些相关策略。

策略1 无控制策略(NC)

在无控制策略情况下，车辆在道路正常运行，此策略是一种不会因等待其它相关线路上的乘客才去增加调度时间的方法。

策略2 简单调度策略(SH)

简单滞站策略与基于时刻表的策略有关。在这种策略下，车辆遵循自己的时刻表，且驶离换车站点的时间，不得早于时刻表。

策略3 基于HMP模型的预测到达时间的车辆动态调度策略(D-HMP)

在D-HMP策略中，发车时间取决于HMP模型对到达时间的预测结果。

策略4 基于SVM模型的预测到达时间的动态车辆调度策略(D-SVM)

在D-SVM策略中，发车时间取决于SVM模型对到达时间的预测结果。

本文分别采用上述4种调度策略对高峰时刻枢纽站点处的所有公交车辆进行了调度优化，结果如图5所示。

图5 四种预测方法的性能比较

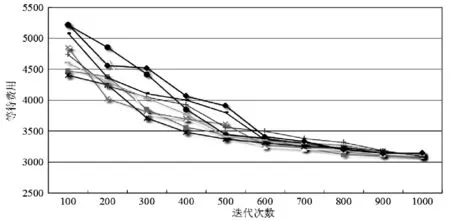
图6 测试结果

从图5可以看到，NC，SH，D-HMP，D-SVM策略的乘客等待时间分别为4778min，4422min，3288min和2997min。在NC策略下，在换乘站点处的乘客所花费的等待时间(4778min)及下游站点的乘客所花费等待时间之和都是最长的，这是因为在NC策略中没有考虑到早到的车辆，从而导致许多乘客没有赶上当前车辆，而不得不花费很长时间等待下一车辆。所以，NC策略造成换乘站点的等待时间长于其他策略的等待时间很多。但是，在NC策略下可以发现下游站点的等待时间为0，这是因为在换车站点时车辆没有增加调度时间，所以在下游站点的乘客则不存在额外的等待时间。而在SH策略下，与NC策略相比，下游站点的等待时间(178min)以及所有乘客的等待时间都较少。并且在SH策略中，无论车辆是否早到，都需要按照时刻表上的规定时间发车，这样的方式使乘客在下游的等待时间增加。不过尽管SH策略在下游的站点产生了额外的等待时间， SH策略仍可以在一定程度上减少换乘乘客错失当前车的几率。但是，在高峰时段只有很少的早到车辆，这使得SH策略不能很好地指引车辆进行换乘线路之间的衔接。D-HMP策略的调度结果比NC和SH策略减少了16.8%和10.1%的乘客等待时间。但D-HMP只是以历史数据作为预测车辆到达时间的依据，不能体现实时的交通状况。相比而言，D-SVM策略调度结果最好，通过计算发现D-SVM策略依次比其他三种策略(NC策略，SH策略，D-HMP策略)减少了24%，17%和8%的乘客等待时间。这是因为，D-SVM策略能较准确地预测换乘线路上车辆的到达时间，可以减少换乘站点的无效调度时间和逐渐减少换乘乘客赶不上当前车辆的情况的发生。显然，D-SVM策略是在换乘站点进行车辆动态调度的有力工具。

最后，本文检验了所提出的算法效率，在相同的参数下对本文的模型连续进行了10次试算，如图6所示。从优化的结果可以看出，乘客的总等待时间随迭代次数增多逐渐下降，运行到一定代数后乘客等待时间几乎不变。进一步发现在前600次迭代计算过程中，乘客等待时间下降比较快，但运行到900次时，乘客的等待时间几乎没有改变，表明算法的收敛性很好。

5 结语

本文针对公交车辆在枢纽的运营调度策略进行了深入研究。由于在枢纽点进行车辆调度不但会使下游站点聚积更多的乘客，而且可能会对相连线路上的换乘乘客的等待时间产生影响，因此，在枢纽点对某辆车进行调度时，需要考虑两个方面等待时间的影响：一方面，确保枢纽点上更多的乘客能赶上这辆车以减少他们的等待时间；另一方面，在枢纽点进行调度可能加大下游站点乘客的等待时间。本文提出了以减少乘客的总等待时间最大化为目标的枢纽动态调度模型。为了更好地预测线路上的车辆运行情况，引入了基于支持向量机的模型来预测预计到达站点时间。根据预计到达时间，动态地对车辆进行调度，可以最大化地减少乘客的总等待时间。

[1] Ling K, Shalaby A. Automated transit headway control via adaptive signal priority[J]. Journal of advanced transportation, 2004, 38(1): 45- 67.

[2] Ting C J, Schonfeld P. Dispatching control at transfer stations in multi-hub transit networks[J]. Journal of Advanced Transportation, 2007, 41(3): 217-243.

[3] Lam S W, Tang L C, Goh T N, Halim T. Multiresponse optimization of dispatch rules for public bus services[J]. Computers & Industrial Engineering, 2009, 56(1): 77- 86.

[4] Chowdhury S M, I-Jy Chien S. Intermodal transit system coordination[J]. Transportation Planning and Technology, 2002, 25(4): 257-287.

[5] Chowdhury M S, Chien S I J. Dynamic vehicle dispatching at the intermodal transfer station[J]. Transportation Research Record: Journal of the Transportation Research Board, 2001, 1753(1): 61- 68.

[6] Dessouky M, Hall R, Zhang L, Singh A. Real-time control of buses for schedule coordination at a terminal[J]. Transportation Research Part A: Policy and Practice, 2003, 37(2): 145-164.

[7] Higgins A, Kozan E, Ferreira L. Optimal scheduling of trains on a single line track[J]. Transportation Research Part B: Methodological, 1996, 30(2): 147-161.

[8] Zhao J, Dessouky M, Bukkapatnam S. Optimal slack time for schedule-based transit operations[J]. Transportation Science, 2006, 40(4): 529-539.

[9] Ting C J, Schonfeld P. Schedule coordination in a multiple hub transit network[J]. Journal of urban planning and development, 2005, 131(2): 112-124.

[10] Ding Y, Chien S. The prediction of bus arrival times with link-based artificial neural networks[C]//Proceedings of the international conference on computational intelligence and neurosciences(CI&N)—intelligent transportation systems. Atlantic City, New Jersey. 2000: 730-739.

[11] Chien S I J, Ding Y, Wei C. Dynamic bus arrival time prediction with artificial neural networks[J]. Journal of Transportation Engineering, 2002, 128(5): 429- 438.

[12] Chen M, Liu X, Xia J, Chien S I. A dynamic bus-arrival time prediction model based on APC data[J]. Computer-Aided Civil and Infrastructure Engineering, 2004, 19(5): 364-376.

[13] Yao B Z, Yang C Y, Yao J B. Tunnel surrounding rock displacement prediction using support vector machine[J]. International Journal of Computational Intelligence Systems, 2010, 3(6): 843- 852.

[14] Yao B Z, Yao J B, Zhang M H. Multi-step-ahead prediction for tunnel surrounding rock displacement using support vector machine[J]. Scientia Iranica, in press. (2013)

[15] Yao B Z, Hu P, Lu X H, Gao J J, Zhang M H. Transit network design based on travel time reliability[J]. Transportation Research Part C, DOI:10.1016/j.trc.2013.12.005, in press.(2013)

[16] Yu B, Yang Z Z, LI S. “Real-time partway deadheading strategy based on transit service reliability assessment”[J]. Transportation Research Part A, 2012, 46(8): 1265-1279.

[17] Yu B, Yang Z Z, Chen K, Yu B. A hybrid model for bus arrival time prediction[J]. Journal of Advanced Transportation, 2010, 44(3): 193-204.

[18] Vapnik V N. An overview of statistical learning theory[J]. Neural Networks, IEEE Transactions on, 1999, 10(5): 988-999.

[19] Vapnik V. The nature of statistical learning theory[M]. springer, 2000.

[20] 姚宝珍,于滨,杨忠振.基于公交车到站时间预测的动态滞站调度模型[J].北京工业大学学报,2011,37(6):869- 875.

[21] Yu B, Yang Z Z. “An ant colony optimization model: the period vehicle routing problem with time windows”[J]. Transportation Research Part E, 2011, 47(2): 166-18.

[22] Yu B, Yang Z Z, JIN P H, Wu Hua S, Yao B Z. Transit route network design using ant colony optimization[J]. Transportation Research Part C, 2012, 22: 58-75.

[23] Yu B, Zhu H B, Cai W J, Ma N, Yao B Z. Two-phase optimization approach to transit hub location the case of dalian[J]. Journal of Transport Geography, 2013, 33: 62-71.

[24] 陈彦如,蒲云.用遗传算法解决固定需求交通平衡分配问题[J].西南交通大学学报,2000,35(1):44- 47.

Multiline Transit Coordination at a Hub Based on Bus-arrival Time Prediction

YU Bin, CUI Yao, CAI Wan-jun, MA Ning

(TransportationManagementCollege,DalianMaritimeUniversity,Dalian116026,China)

Due to the poor prediction of traditional scheduling model, a SVM-based prediction model is put forward to forecast the arrival time of public transport vehicles at the transfer station. Then a scheduling model aimed at reducing the total waiting time of passengers is constructed to dynamically coordinate the departure time at the transfer station. Genetic Algorithm is applied to solve the dynamic scheduling problem in this paper. Finally, this paper verifies the feasibility of the model and algorithm with the data of Shahekou station in Dalian city. And the results show that the scheduling method this paper proposed is superior to the traditional scheduling method.

transportation planning and management; bus dynamic vehicle scheduling; arrival time prediction; SVM(support vector machine)-based model; genetic algorithm

2013- 01- 05

国家自然科学基金青年基金项目(51108053)；教育部新世纪人才支持计划 (NCET-12- 0752)；辽宁省高等学校优秀科技人才支持计划( LJQ2012045)

于滨(1977-)，男，教授。

U492

A

1007-3221(2015)04- 0246- 08