新产品定价决策的影响因素分析

蒋紫艳， 赵 军

(1.上海交通大学 安泰经济与管理学院，上海 200052； 2.宁夏大学 经济管理学院，宁夏 银川 750021)



新产品定价决策的影响因素分析

蒋紫艳1， 赵 军2

(1.上海交通大学 安泰经济与管理学院，上海 200052； 2.宁夏大学 经济管理学院，宁夏 银川 750021)

新产品的成功销售取决于两个重要的因素：一是具有生产特性的工程变量，比如产品的可靠性水平；一是具有市场特征的影响因素，比如价格和保障机制。为了实现收益，制造商必须认真审视价格、产品可靠性和保障机制的选择。因此，本文将价格作为外生变量，将保障机制与可靠性作为决策变量，建立了以最大化为目标的收益模型，分析可靠性与保障机制的最优策略。另外，探讨当不同变量的敏感性参数发生变化时，最优保障机制与产品可靠性的变化规律。最后，通过算例分析收益函数的基本特性，结论显示消费者总是从产品保障机制的信号中判断产品的可靠性水平，这对新产品销售有一定的借鉴意义。

企业管理；定价；确定性线性规划方法；保障机制；可靠性水平

0 引言

新产品的收益管理一直是学者关注和研究的焦点，尤其针对新产品在投入市场时面临的诸多问题，最为关键的是销售[1]。Huang，Liu和Murthy[2]指出影响新产品成功销售的因素包括工程制造因素(如可靠性水平)和市场因素(如价格和保障机制)。由于产品更新换代地不断加速，在技术和性能设计上是越来越复杂，消费者无法明确自身对产品的具体需求，而其购买意愿往往取决于产品的性价比。从产品销售的市场经验可获知，向消费者传递产品质量和性能信息的一个重要手段是提供相应的售后保障机制。正如Blischke和Wallace[3]、Murthy和Djamaludin[4]指出消费者在做出购买决定之前，通过产品制造商所传递的关于售后保障机制这样的信号，来判断产品的性能(如可靠性水平)。那么，在面对不同的市场环境时，制造商应如何确定产品的可靠性水平，以及相应的保障机制，从而实现收益最大化。另外，当影响销售的因素发生变化时，最优的可靠性水平和保障机制呈现怎样的变化规律，是文中重点解释的问题。

1 新产品销售的影响因素分析

从消费者的角度分析，消费者往往倾向于支付较高的价格购买质量有保证和性能更为完善的产品，从而获取更大的消费者剩余价值。由生产实践可知新产品的工程制造因素(如可靠性水平)取决于制造成本投入的程度，在此的假设与Jeyakumar和Robert[5]相同，即较大的投入将会实现较高的可靠性，必然也会导致较高的销售价格。那么，制造商在生产环节的投入称为制造成本。另外，生产经验显示可靠性水平提高可以降低产品退换或者损坏的概率，从而降低保障成本，反之亦然。

保障机制是买卖双方关于销售产品的协约式合同[3]，是产品制造商以成功销售产品，提高顾客满意度为目的，向消费者提供的关于产品可以退换或者维修的承诺。消费者认知产品可靠性水平的方法是通过制造商提供的售后服务的信息进行判断的，即保障机制(Warranty Policy)。Murthy和Djamaludin对以往的研究进行了综合性地阐述分析，指出一些学者从不同的角度对产品保障机制进行了研究。其中许多学者认为保障机制是与工程制造因素紧密联系的，比如通过知识积累、研发、技术改进、维护、产品测试等手段提高产品性能，满足消费者对产品的需求，从而也实现了制造商的最大化利益。最有代表的文献资料包括Teng和Thompson[6]，Hussain和Murthy[7]，以及Shue和Chien[8]。从市场销售实践中可知较好的保障机制往往证实产品具有较高的可靠性水平，否则制造商将承担较大的风险，包括产品退换、损坏维修的风险，或者信誉和品牌形象损失的风险，甚至可能还会为弥补损失付出更大的代价。另外，较好的保障机制会促进销售，产生网络外部性(Network externality)的效应，但同时也带来了额外的保障成本。文章依据制造商收益最大化为目标，尝试性地建立包含价格、可靠性水平和保障机制三个变量的收益函数，对销售市场环境的影响参数进行定义，具体分析最优的可靠性水平和保障机制随着敏感度参数变化的特性。

在新产品的收益管理研究中，较早的文献通过建立静态模型进行分析，把价格、可靠性和保障机制作为产品销售的三个影响变量，从而确定其收益水平。Teng和Thompson[6]对静态模型进行了拓展，依据学习理论，将价格和质量水平作为决策变量，建立动态规划模型分析最优策略，并且证明了产品质量成本随着技术知识的积累是逐渐降低的曲线。Lin和Shue[9]，以及 Wu、Lin和Chou[10]改进了动态收益模型，将价格和保障期限作为决策变量，分析产品生命周期服从多种分布的收益情况。最近，Li、Mallik和Chhajed[11]探讨了整个供应链系统中最优的价格和保障机制。Wang和Liu[12]对保障机制进行了概念上的拓展，分析了静态与动态的最优机制。那么，这篇文章与以往文献相同的是选择经济学视角，并将产品可靠性水平和保障机制作为决策变量，但是区别在于对这两个决策变量的环境影响因素进行了具体的定义，即设定敏感性参数，探讨以收益最大化为目标时，可靠性水平和保障机制的最优策略，并且随外生变量(即价格)和环境因素变化的基本特性，从而在所得的结论中获取实践上的意义。

2 问题描述及模型建立

2.1 需求函数

Huang，Liu和Murthy[2]分析消费者常常参照保障信息来判断产品的可靠性水平，判断价格是否合理，指出由于产品的可靠性水平是由制造环节决定的，在销售期间并不能直接被消费者感知，所以它对购买决策没有影响。因此，价格和保障机制成为决定产品销售的两个重要因素，需求量D是关于价格p和保障机制ω变量的函数，表示如下：

D=f(p,ω)

(1)

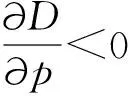
为了便于后面的分析，参考Tsay和Agrawal[13]，即产品的需求量是价格和保障机制的线性关系，表示如下:

D=α-αpp+αωω

(2)

其中，参数α，αp和αω均大于0。α表示依赖于产品质量、竞争环境、品牌效应等经济因素的主要产品需求。αp表示价格的敏感度参数，很明显，在基本需求量α的基础上，当价格增加时，需求就以变化速度为αp的值而减少。αω是保障机制的敏感度参数，当保障机制增加时，需求量在基本需求α的基础上以变化速度αω增加。

2.2 可靠性水平的成本分析

产品的可靠性水平是由研发、设计和技术等生产要素决定的，其成本与制造投入的程度有关，假设可靠性水平的变量为θ，参照Buratto和Viscolani[14]对质量成本的解释，产品可靠性水平的成本是关于θ递增的凸函数，并且关于可靠性水平的一阶和二阶导数均大于零，即C′>0，C″>0,，可以表示如下：

(3)

其中，ψ表示可靠性的敏感度参数，ψ>0。

2.3 保障的期望成本分析

根据消费者保护权益，保障机制是在满足一定的条件下产品可以在保障期限内被退回或者返修。当产品被退换或返修时，必然会产生额外的成本，比如传输成本、再次确认成本、时间成本和劳动力成本等，甚至造成一些损失，比如声誉受损、品牌确实等，在这里将与这些有关的成本统一用“保障成本”表示，实践中一些种类保障成本并不明确。因此，Blischke和Murthy[3]定义保障成本是一个随机变量。考虑到“保障成本”的复杂性，将其分为两种类型：一种是产品在保障期限内退换或损坏所带来的维修成本，表示为C1(θ,ω)；另一种是为弥补相关损失带来的成本，表示为C2(ω)。

首先，依据Blischke和Murthy[3]建立维修成本的函数形式，与维修策略有关，是关于产品维修期限S(θ,ω)的函数。那么，维修期限应是产品可靠性水平的减函数，期望的维修成本函数表示如下：

C1(θ,ω)=υS(θ,ω),S(θ,ω)=(1-ηθ)ω

(4)

其中，υ表示维修的期望成本，η表示产品损坏概率的敏感度参数(υ>0,η>0)。可知，可靠性越高，产品需维修的概率越低，需要维修的期限越短，维修成本将越低。

其次，第二种成本来源于为弥补损失产生的成本，主要包括挽回品牌信誉、挽留消费者、防止售后服务资源浪费和提高顾客满意度等，所以与售后服务有关，其形式表示如下：

(5)

其中，γ表示对弥补损失成本的敏感度参数，γ>0，以上两种成本形式全面构成了“保障成本”。

2.4 收益函数的模型分析

以上对各变量进行了定义，假设市场有一垄断制造商的收益取决于价格、销售量、制造成本和保障机制四个重要因素。因此，受益函数可以表示成：

π=pD(p,ω)-C(θ)-C1(θ,ω)-C2(ω)

(6)

其中，pD(p,ω)表示总收益，净收益即为总收益减去可靠性成本和保障成本。在这里认为价格为外生变量，收益函数中D(p,ω)，C(θ)，C1(θ,ω)和C2(ω)，以及各敏感性参数均可由上文中的公式带入，表示形式如下：

(7)

这里将影响收益的保障机制与可靠性水平作为决策变量进行分析，但从式(7)中并不能直接获取相关的影响特性，主要是因为如果增加一个变量，另一个变量的变化具有不确定性。因此，可以通过建立收益最大化的目标，分析最优的保障机制与可靠性的基本特性。

3 模型求解与分析

这部分对收益函数，以及保障机制与可靠性两个决策变量进行深入分析，并且探讨保障机制与产品可靠性针对敏感性参数变化所呈现的性质，即这些参数变化时，采取的最优策略将如何变化。在具体分析之前，假设αωp-υ>0，即在保障机制的影响下，边际收益始终为正，这使以下证明有意义。

命题1 只要条件ψγ-η2υ2>0满足，收益函数是严格凹函数，而且有唯一最大值。

命题2 在满足命题1的条件下，可靠性和保障机制的最优策略分别表示如下：

(8)

(9)

证明 使收益函数对可靠性θ和保障机制ω求一阶偏导，并设定为0，则可得

然后进行代数运算，可获得含有敏感度参数的最优可靠性和保障期限，最优的策略可表示如下：

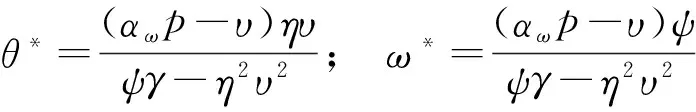
由命题2可知，制造商在制定合理的保障机制，或者可靠性时，需充分考察每个变量的敏感度参数如何影响着最优的结果，目的在于提高一些管理策略的引导，以下具体进行分析。

命题3 市场上消费者的需求对保障机制的敏感度越大，即αω增加，那么制造商需提供更好的保障机制，同时最优的可靠性水平也应该随之提高。

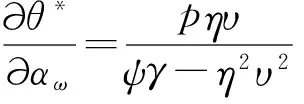
命题3和市场上的实际现象是一致的，当消费者获知了具体的产品保障机制，并且对产品的可靠性进行判断，他们总是期望信息的真实可靠，也就是较好的保障机制必然应该伴随着较高的可靠性水平。

命题4 当消费者对可靠性成本的敏感度降低时，最优的可靠性水平将增加，同时对应的保障机制也应提升。

命题5 当弥补损失成本的敏感度降低时，最优的可靠性水平将增加，同时保障机制也将提升。

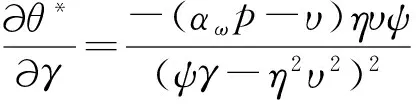
命题4和命题5说明了当与可靠性成本和弥补损失成本的敏感度参数降低时，制造商应该提升保障机制和提高产品的可靠性水平，从而促进销售，提高收益。那么，成本的敏感度参数也成为了决定销售策略的一个重要指标。

命题6 当损失概率的敏感度增加时，或者期望成本提高时，最优的可靠性水平与保障机制均应提高。

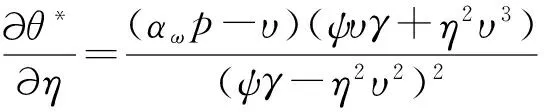
命题6指出消费者如果对产品购买后损坏的情况敏感度较高时，所对应的保障机制与可靠性水平都应该提高。另外，应该通过提升保障机制与可靠性水平，降低维修的概率，从而降低维修成本。

命题7 当外生变量价格提高时，最优的可靠性水平与保障机制均应提高。

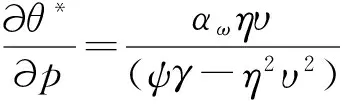
命题7意味着与提高价同时进行的是应该提升保障机制，以及提高产品的可靠性水平。

表1 外生变量和敏感度参数的取值

参数数值价格p60需求依赖外生变量的敏感度参数α100价格敏感度参数αp1保障机制敏感度参数αω0.5可靠性设计成本的敏感度参数ψ25损坏概率的敏感度参数η0.5损坏的期望成本参数υ15弥补损失成本的敏感度参数γ10

4 数值算例与计算

上文分析了保障期机制与可靠性水平在收益最大化的条件下，针对敏感性参数的变化时的相关特性。根据上文的假设条件，针对ω和θ，下面运用数值计算方法对收益进行分析，给出新产品在投放市场时一些借鉴性的方法，设各参数的取值如表1所示。

当可靠性水平θ分别为0.5,0.6,0.7，并且在每一取值中保持不变，假设保障机制ω逐渐提升时，收益函数的变化趋势如图1所示。由图1可知收益函数是递增的凹函数，同时在给定产品的可靠性水平时，随着保障机制的提升，收益也是增加的。那么，也就是说较好的保障机制将会产生较高的收益。

当保障机制ω分别为0,1,2时，并且在每一取值中保持不变，假设可靠性水平θ是逐渐提高的，收益的变化趋势如图2所示，可知收益函数是凹函数，但收益的变化却有可能出现递减的情况。由此的解释是当保障机制低于消费者期望时，即使可靠性水平θ提高，由于消费者对产品性能不能做出准确的判断，收益就会逐渐递减。当保障机制ω提高后，当达到一定的消费者期望之上时，收益函数才会随着保障机制的提升而增加。因此，保障机制是向消费者传递产品可靠性水平的一个重要信号。

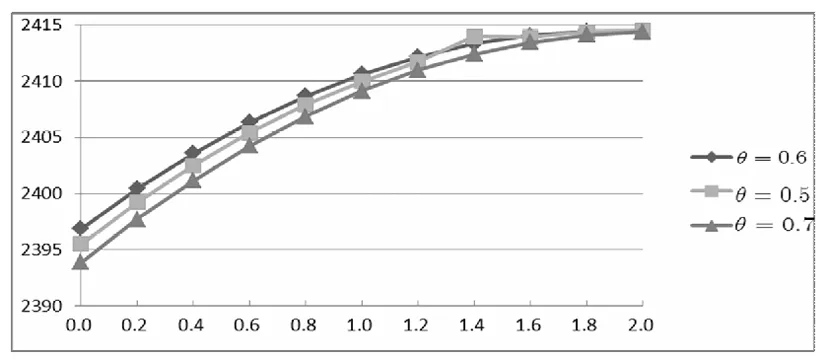
图1 可靠性水平给定情况下的收益函数变化趋势图

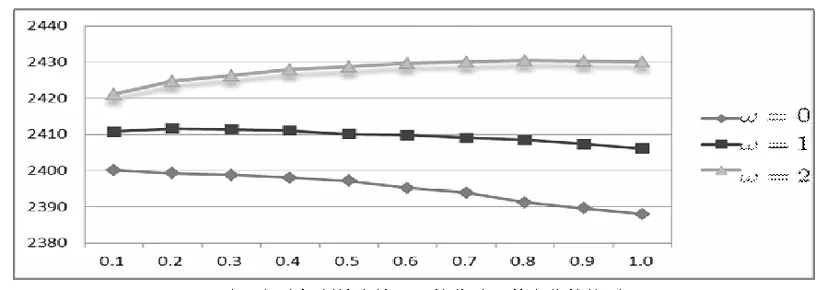
图2 保障机制给定情况下的收益函数变化趋势图

5 总结

影响新产品销售的因素有很多，本文选择了两个最为重要的因素进行分析，一是保障机制，一是产品的可靠性水平，建立收益模型分析这两个决策变量。由以上分析可知，消费者在认知产品性能指标时，往往是从销售商提供的售后保障进行判断的，即保障越好，产品的可靠性水平越高，反之亦然，从而会影响产品的销售，而这两个重要的影响因素也会产品定价的变化而变化。因此，销售商在制定营销策略时，需同时考虑这三个因素及相互作用，并且需对消费者的价值期望做出正确的判断。

[1] 杨锦棠，陈仪渠.影响产品销售量的因素[J].南方经济,1985,6:47-53.

[2] Huang hong zhong, Liu zhi jie, Murthy D N P. Optimal reliability, warranty and price for new products[J]. IIE Transactions, 2007, 39(8): 819- 827.

[3] Blischke W R, Murthy D N P. Product warranty handbook marcel dekker[M]. New York, 1996. 158-177.

[4] Murthy D N P, Djamaludin I. New product warranty: a literature review[J]. International Journal of Production Economics, 2002, 79: 231-260.

[5] Jeyakumar Robert K, Paul T. Joint determination of price, warranty length and production quantity for new products under free renewal warranty policy[C]. Center for Quality, 2010. 105-114.

[6] Teng J T, Thompson G L. Optimal strategies for general price quality decision models of new products with learning production costs[J]. European Journal of Operational Research, 1996, 93: 476- 489.

[7] Hussain A Z M O, Murthy D N P. Warranty and optimal reliability improvement through product dvelopment[J]. Mathematical and Computer Modeling, 2003, 38: 1211-1217.

[8] Shue S H, Chien Y H. Optimal burn-in-time to minimize the cost for general repairable products sold under warranty[J]. European Journal of Operational Research, 2005,163: 445- 461.

[9] Lin P C,Shue L Y.Application of optimal control theory to product pricing and warranty with free replacement under the influence of basic life time distributions[J]. Computer and Industrial Engineering, 2005, 48: 69- 82.

[10] Wu C C, Lin P C, Chou C Y. Determination of price and warranty length for a normal lifetime distributed product[J]. International Journal of Production Economics, 2006, 102: 95-107.

[11] Li K S, Mallik D, Chhajed. Design of extended warranties in supply chains under additive demand[J]. Production and Operations Management, 2012, 21(4): 730-746.

[12] Wang X, Liu L. Optimal reliability, warranty length, price and service quality for repeat purchase products[C]. The 19th International Conference on Industrial Engineering and Engineering Management, 2013, 917-927.

[13] Tsay A, Agrawal N. Channel dynamics under price and service competition[J]. Manufacturing and Service Operations Management, 2000, 2(4): 372-391.

[14] Buratto A, Viscolani B. New product introduction: Goodwill, time, and advertising cost[J]. Mathematics Methods of Operations Research, 2002, 55(1): 55- 68.

Analysis Factors Influencing Pricing Decision of New Products

JIANG Zi-yan1, ZHAO Jun2

(1.AntaiCollegeofEconomics&Management,ShanghaiJiaoTongUniversity,Shanghai200052,China; 2.SchoolofEconomics&Management,NingxiaUniversity,Yinchuan750021,China)

The sales of new product depend on two important factors: one is the engineering variables with production characteristics, such as the level of reliability; the other one is the market factors, such as price and warranty policy. A higher reliability results in a higher manufacturing cost and higher sale price. Consumers are willing to gain a higher reliability only if the price may be higher. They often judge the level of products reliability by the information of warranty policy, in order to decide whether to buy or not. Manufacturer increases demand by establishing better warranty strategy, but at the same time bears additional costs. Therefore, with price as the exogenous variable, the paper proposes a model to determine the optimal product reliability and warranty strategies which are decision variables, for the maximum benefit. Moreover, when the sensitivity parameters of the different variables change, the model will discuss the regulation of the optimal warranties strategy and product reliability. Finally, the example analyses the basic characteristics of the revenue function. The conclusion shows that consumers always judge the reliability level of products from the signal of warranty policy, which is significant for selling new products.

enterprise management; pricing; choice deterministie linear programming method; warranty policy; level of reliability

2013-12-18

蒋紫艳(1980-)陕西西安人 宁夏大学经济管理学院 讲师，上海交通大学安泰经济管理学院在读博士研究生， 研究方向：收益管理、动态定价；赵军 宁夏大学经济管理学院 副教授 硕士生导师 研究方向：信息系统 管理决策

F272.3

A

1007-3221(2015)04- 0240- 06