城市公共设施事故应急资源配置优化模型

刘近远， 李 垚， 闫 凯

(1.黑龙江大学，黑龙江 哈尔滨 150080; 2.中国科学院大学，北京 100190; 3.内蒙古大学，内蒙古 呼和浩特 010021)



城市公共设施事故应急资源配置优化模型

刘近远1， 李 垚2， 闫 凯3

(1.黑龙江大学，黑龙江 哈尔滨 150080; 2.中国科学院大学，北京 100190; 3.内蒙古大学，内蒙古 呼和浩特 010021)

城市公共设施事故发生时,迅速调动应急资源，尽早展开救援，对促进社会发展和保持社会稳定具有重要意义。本文根据城市公共设施突发事故中资源配置问题的特点，运用多目标规划的思想，建立了应急资源配置的多目标规划模型，并通过实验模拟对模型进行了求解验证。此模型可以成功实现城市公共设施事故应急资源的有效配置，为相关部门的决策提供理论指导。

资源配置；多目标规划; 应急决策；优化模型

0 引言

众所周知，突发灾害事件具有很大的不确定性, 发生时间、发展途径和演变规律以及危害程度等难以预计, 但是破坏性很大；可能对生命财产和基础设施造成严重损害或重大生态环境破坏,从而对国家经济发展、社会稳定和政治安定造成严重冲击,所以对于突发事件应急决策的研究一直是各国政府十分重视的问题[1]。在各类突发事件中，常规的水、气等管道破裂、电力及交通设施设备故障等城市公共设施突发事件虽然可能持续时间一般较短, 影响范围一般不大，但发生的频率相对较高，与城市居民的日常生活息息相关。如果不能及时处理, 小事件可能演化、衍生出新的事件, 以至于可能造成较大损失甚至可能会导致突发公共事件。例如, 雷击可能会导致大面积的停电事件, 而停电事件又可能导致交通信号指挥系统中断, 从而导致大规模的交通拥堵事件等[1]。随着人们对应急管理及其在经济增长中作用的认识，实现应急资源的优化配置，最大限度地发挥应急资源的优势，促进国家、地区经济的持续增长，成为越来越多的国家和地区开始关心并研究的问题[2]。突发事件发生以后，需要大量的救灾物资对事件进行紧急处理，这种应急问题最显著的特点就是时间的紧迫性，其时间效益高于经济效益。然而在进行物资配置的过程中要尽量做到在短时间内保障物资供应的同时兼顾救援成本问题[3,4]。突发事故发生时,如何迅速调动应急资源，尽早到达事故地点展开救援工作，最大限度减少损失，具有重要意义。目前对突发事件应急资源配置的研究成果已广泛运用于火灾、地震、矿井塌陷以及辐射性废料泄漏事故等具体灾害领域[5～8]。事故发生时，通常的应急反应思路是：让最近的出救点参与应急[8,9]。这里暗示了一个假设，即事故点所需的应急资源量不能大于每个供应点的供应能力。但是，当大的灾难或事件发生时，仅一个出救点一般不能提供应急所需的大量物资，于是产生了多出救点的组合出救问题[9]。另外，城市公共设施事故的发生具有不确定性，往往有多个事故点同时需要救援。因此，如何对多个点的应急资源进行合理配置，达到时间最短、成本最低的目标，在城市公共事故应急资源配置中具有重要的意义。

1 问题描述

在事故发生时人们面对的一个重要问题便是如何有效地利用有限的运输工具向事故地点及时输送救援人员及救援设备。现实中往往会遇到存在多个救援物资供应点的情况，这时如何确定各供应点需要提供的资源数量，达到最佳的救援效果以及最好的经济利益，成为需要调度人员解决的关键问题。假设事故点周围一共有m个供应点，第i个供应点有Mi个人，Ni个设备.事故发生以后需要p个人和q台设备到达现场。现在的问题是：如何从这m个供应点调度资源，实现资源调度最优化？设第i个供应点距离事故点的距离为ai，从第i个供应点出发到事故点的人力成本为每单位bi，物力成本为每单位ci。

2 单一事故点的应急资源配置优化模型模型

首先只考虑成本因素，假设现在要从第i个供应点调度xi个人，yi台设备。最优化模型建立如下：

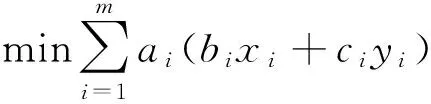
上面考虑的是成本因素，如果单独考虑时间因素可以建立下面的优化模型。设供应点i到事故点的时间为ti，zi为指示变量，如果从第i个资源点调度物力或者人力的话，则为1，否则为0。

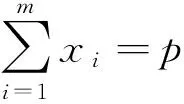
应急资源配置中需要考虑的因素很多，对于每个因素都可以建立相应的目标函数F，并对其进行最大或者最小优化。因此，可以得到对单一因素的资源调度问题优化模型的一般框架如下：

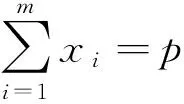
综合各种因素，就可以得到关于T个目标的资源调度问题的多目标优化决策模型如下：

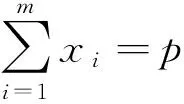
比如，综合考虑成本和时间因素，就可以得到相应的多目标优化模型如下：

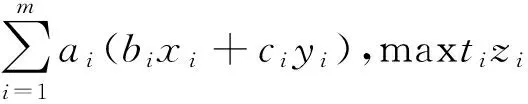
在生产、经济、管理、科学和工程活动中，经常需要对含有多个目标的方案进行决策，这不同于单目标的决策。单目标的决策需要在满足约束条件的情况下，找到使目标函数取极值的解。而多目标的决策往往需要在满足约束条件的情况下，在各个目标之间进行权衡。比如，设计一个导弹，既要其射程远，又要耗燃料少，还要命中率高等；又如，对企业产品的生产管理,既希望达到高利润,又希望优质和低消耗,还希望减少对环境的污染等[10]。可见，只有对各种因素的指标进行综合衡量后，才能做出合理的决策。

由于直接求解多目标规划问题比较困难，因此需要对多目标规划问题进行适当的处理。常见的处理方法主要有两种：第一种是化多为少的方法，也就是将一个多目标规划根据某些原则转化成一个单目标规划，再利用已知的单目标规划的求解方法求解，如主要目标法、线性加权法、理想点法等；第二种是把多目标规划看成是许多个单目标规划的集合，通过依次求解每个单目标规划得到最后的解，如分层序列法等。多目标规划问题已经被转化为了单目标的整数规划模型求解问题，分枝定界和割平面是最常用的两种求解整数规划的方法[10]。

3 多事故点的应急资源配置优化模型

以上讨论的是只有一个事故点的情况，而实际上往往出现多个事故点同时需要资源调配的情况，此时需要将原模型进行推广。假设有n个事故点需要救援，一共有m个供应点，第i个供应点有Mi个人，Ni个设备.事故发生以后，第j个事故点需要pj个人和qj台设备到达现场。现在的问题是：如何从这m个供应点调度资源，实现资源调度最优化？设第i个供应点距离第j个事故点的距离为aij，从第i个供应点出发到第j个事故点的人力成本为每单位bij，物力成本为每单位cij。

首先只考虑成本因素，假设现在要从第i个供应点调度xij个人，yij台设备到第j个事故点。最优化模型建立如下：

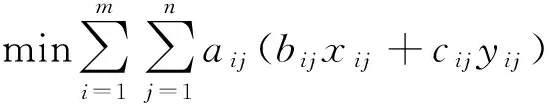
上面考虑的是成本因素，如果单独考虑时间因素可以建立下面的优化模型。设第i个供应点到第j个事故点的时间为tij，zij为指示变量，如果从第i个资源点调度物力或者人力到第j个事故点的话，则为1，否则为0。

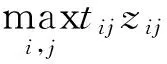
类似的，对于多个事故点的资源调度问题，多目标优化决策模型如下：

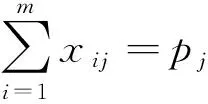
5 实验模拟

5.1 单个事故点的资源配置

案例：某城市发生了燃气管道爆炸事故，现需要立即进行抢修。假设事故抢险工作需要100个人以及20台救援设备，现可从事故发生位置附近的市燃气公司的3个应急抢险队A，B，C调集人力与设备。已知各抢险队与事发地的距离、从各抢险队调集资源的人力与物力成本、各抢险队到达事发地所需时间以及各抢险队的可用人数和可用设备数(如表1所示)。另外，只有当所需要的人力、物力资源全部到位时，抢修工作才能开始。如果想使抢险工作的成本最低，同时保证抢险工作能尽快开始，请问应该如何从各抢险队调集人员与设备？

表1 各抢险队的相关数据

求解过程：通过对上述实际问题的分析，可以确定这是一个多目标决策的问题，共有两个目标：一个是成本最低，另一个是时间最短。根据问题数据建立模型如下：

成本最低目标：

min 300x1+600y1+560x2+980y2+500x3+1000y3s.t.x1+x2+x3=100y1+y2+y3=20 0≤x1≤30 0≤x2≤60 0≤x3≤50 0≤y1≤20 0≤y2≤20 0≤y3≤10x1,x2,x3,y1,y2,y3∈Z

时间最短目标：

min maxtizis.t.x1+x2+x3=100y1+y2+y3=20xi>0 oryi>0,zi=1, otherwisezi=0(i=1,2,3) 0≤x1≤30 0≤x2≤60 0≤x3≤50 0≤y1≤20 0≤y2≤20 0≤y3≤10x1,x2,x3,y1,y2,y3∈Z

可以应用多目标决策的方法来求解。这里我们分别利用主要目标法以及分层序列法这两种方法对模型进行求解。

主要目标法：应急事故自然时间最短是主要目标，所以可以进行如下处理：对成本这个目标设定一个上界，比如根据经验取上界为65000元，则对于时间最短这个目标，增加了一个约束：

300x1+600y1+560x2+980Y2+500x3+1000y3≤65000

问题转化为：

min maxtizis.t. 300x1+600y1+560x2+980Y2+500x3+1000y3≤65000x1+x2+x3=100y1+y2+y3=20xi>0 oryi>0,zi=1,otherwisezi=0(i=1,2,3) 0≤x1≤30 0≤x2≤60 0≤x3≤50 0≤y1≤20 0≤y2≤20 0≤y3≤10x1,x2,x3,y1,y2,y3∈Z

由于A、C两抢险队人数之和不足100，故B抢险队必定要参加抢险工作，此时不论如何调集资源，所需时间均为15分钟。

故只要满足约束条件的解均是最优解，此时问题转化为求解如下的不等式组：

由于最优解不唯一，这里考虑在此基础上追求成本最低，因此模型转化为：

min 300x1+600y1+560x2+980Y2+500x3+1000y3s.t.x1+x2+x3=100y1+y2+y3=20 0≤x1≤30 0≤x2≤60 0≤x3≤50 0≤y1≤20 0≤y2≤20 0≤y3≤10x1,x2,x3,y1,y2,y3∈Z

用matlab编程求解该整数规划，可得最优解为：需要A抢险队30人、20台设备，B抢险队20人，C抢险队50人前往事发地即可，总成本为57200元，时间为15分钟。

分层序列法：由于时间为主要目标，故首先对时间进行最小化，得到最优解的集合，再以这个最优解集合为取值集合使成本最小化，得到最后的最优解。

求解过程如下：分析可得，由于A、C两抢险队人数之和不足100，故B抢险队必定要参加抢险工作，此时不论如何调集资源，所需时间均为15分钟。故对于时间最短这个目标，最优解的集合就是初始的约束集合，问题转化为求解成本最低这个单目标规划。模型如下：

min 300x1+600y1+560x2+980Y2+500x3+1000y3s.t.x1+x2+x3=100y1+y2+y3=20 0≤x1≤30 0≤x2≤60 0≤x3≤50 0≤y1≤20 0≤y2≤20 0≤y3≤10x1,x2,x3,y1,y2,y3∈Z

用matlab编程求解这个整数规划，可得最优解为：需要A抢险队30人、20台设备，B抢险队20人，C抢险队50人前往事发地即可，总成本为57200元，时间为15分钟。

5.2 多个事故点的资源配置

案例：某城市两个地区先后发生了燃气管道爆炸事故，现需要立即进行抢修。假设第一个事故点的抢险工作需要100个人以及20台救援设备，第二个事故点的抢险工作需要150个人以及30台救援设备。现可从事故发生位置附近的市燃气公司的3个应急抢险队A，B，C调集人力与设备。已知各抢险队与事发地的距离、从各抢险队调集资源的人力与物力成本、各抢险队到达事发地所需时间以及各抢险队的可用人数和可用设备数(如表2所示)。另外，只有当所需要的人力、物力资源全部到位时，抢修工作才能开始。如果想使抢险工作的成本最低，同时保证抢险工作能尽快开始，请问应该如何从各抢险队调集人员与设备？

表2 各抢险队的相关数据

求解过程：通过对上述实际问题的分析，可以确定这同样是一个多目标决策的问题，共有两个目标：一个是成本最低，另一个是时间最短。根据问题数据建立模型如下：

成本最低目标：

min 300x11+500x12+560x21+160x22+500x31+300x32+600y11+1000y12+ 980y21+280y22+1000y31+600y32

s.t.x11+x21+x31=100y11+y21+y31=20x12+x22+x32=150y12+y22+y32=30 0≤x11+x12≤80 0≤x21+x22≤100 0≤x31+x32≤70 0≤y11+y12≤40 0≤y21+y22≤30 0≤y31+y32≤15x11,x12,x21,x22,x31,x32,y11,y12,y21,y22,y31,y32∈Z

时间最短目标：

min maxtijzijs.t.x11+x21+x31=100y11+y21+y31=20x12+x22+x32=150y12+y22+y32=30xij>0 oryij>0,zij=1,otherwisezij=0(i=1,2,3;j=1,2) 0≤x11+x12≤80 0≤x21+x22≤100 0≤x31+x32≤70 0≤y11+y12≤40 0≤y21+y22≤30 0≤y31+y32≤15x11,x12,x21,x22,x31,x32,y11,y12,y21,y22,y31,y32∈Z

我们仍然可以应用主要目标法或分层序列法等多目标规划的方法来求解。这里,我们运用技巧,可以更方便的得到结论。通过分析，两个事故点开始救援所需最短时间的取值可以是5,8,10,15。此时我们考虑每个事故点所需的人员和设备数量，以及各种时间所对应的资源配置方案，可以将5和8排除。然后我们只需要验证关于成本最低的模型在10分钟这个时间约束下是否有最优解，即可得到最终的结果。问题转化为求解如下优化问题：

min 300x11+500x12+560x21+160x22+500x31+300x32+600y11+1000y12+ 980y21+280y22+1000y31+600y32

s.t.x11+x31=100y11+y31=20x21=y21=0x12+x22+x32=150y12+y22+y32=30 0≤x11+x12≤80 0≤x22≤100 0≤x31+x32≤70 0≤y11+y12≤40 0≤y22≤30 0≤y31+y32≤15x11,x12,x21,x22,x31,x32,y11,y12,y21,y22,y31,y32∈Z

利用matlab编程求解，可得最优解为：需要A抢险队往第一个事故点派53人、12台设备，往第二个事故点派27人、11台设备；B抢险队往第二点派100人、12台设备；C抢险队往第一事故点派47人、8台设备，往第二事故点派23人、7台设备。总成本为109560元，时间为10分钟。

6 结论

本文针对城市公共设施事故救援中的资源配置问题，建立了以时间最短、成本最低为目标的多目标的优化模型，并将模型推广到同时存在多个事故点的情况，取得了较好的结果，为城市公共设施事故的资源配置提供了一定的参考依据。对于各供应点到各事故点的时间不确定以及各供应点到各事故点之间存在多条路线的情况还需进一步的研究。

[1] 曹杰，杨晓光，汪寿阳.突发公共事件应急管理研究中的重要科学问题[J].公共管理学报，2007,2:84-93.

[2] 方磊.基于偏好DEA模型的应急资源优化配置[J].系统工程理论与实践，2008，5：98-104.

[3] 刘北林，马婷.应急救灾物资紧急调度的研究[J].哈尔滨商业大学学报：社会科学版，2007，3:3-17.

[4] 高淑萍，刘三阳.应急系统调度问题的最优决策 [J].系统工程与电子技术，2003,10:1222-1224.

[5] Jean-Luc Wybo. FMIS: a decision support system for forest fire prevention and fighting[J]. IEEE Transactions on Engineering Management, 1998, 2: 127-131.

[6] Walter W Hays. Reduction of earthquake risk in the united states: bridging the gap between research and practice[J]. IEEE Transactions on Engineering Management, 1998, 2: 176-180.

[7] Henry P Cole. Decision making during a simulated mine fire escape[J]. IEEE Transactions on Engineering Management, 1998, 2: 153-162.

[8] George List F. Routing and emergency-response-team siting for high-level radioactive waste shipments[J]. IEEE Transactions on Engineering Management, 1998, 2: 141-152.

[9] 刘春林,何建敏,施建军.一类应急物资调度的优化模型研究[J].中国管理科学,2009,3:29-36.

[10] 甘英爱，田丰，李维铮等.运筹学[M].清华大学出版社，2005.

Emergency Resource Allocation Model for Urban Public Facility Accidents

LIU Jin-yuan1, LI Yao2, YAN Kai3

(1．HeilongjiangUniversity，Harbin150080,China；2.UniversityofChineseAcademyofSciences，Beijing100049,China；3．InnerMongoliaUniversity，Hohehot010021,China)

In the face of urban public facility accidents, mobilizing resources quickly and making them arrive at accident location as soon as possible is of great importance to promote social development and maintain social stability. According to the characteristics of urban public facility accidents and the basic idea of multi-objective programming, a multi-objective programming emergency resource allocation model is proposed and proved to be useful after simulated experiment. This model not only can achieve allocation emergency resources effectively, but also provide theoretical guidance for related departments.

resource allocation; multi-objective programming emergency decision；optimization model

2014- 08- 06

刘近远，男，研究方向：应用数学；李垚，男中国科学院大学，研究方向：运筹与管理；闫凯，男，内蒙古大学，研究方向：最优化理论。

C931, O224

A

1007-3221(2015)04- 0068- 08