曳引电梯提升动力学建模及仿真研究
吴仁愿,曹国华,岳 岭
(1.中国矿业大学,徐州 221116;2.东南电梯股份有限公司,苏州 215100)
0 引言
随着经济的快速发展和社会的不断进步,楼层越来越高,曳引电梯也日益朝着大高度高速度发展。振动是影响电梯舒适性的重要因素,对于高速电梯尤为重要。因此,对曳引电梯提升动力学进行研究,在设计阶段掌握曳引电梯的振动情况具有重要的现实意义。
国内外专家学者对曳引电梯的提升动力学做了诸多研究,文献[1~4]建立电梯系统动力学模型时忽略了曳引钢丝绳本身的质量,而将其仅仅看作一个随钢丝绳悬挂长度变化的弹簧-阻尼器;文献[5, 6]将每一段钢丝绳被分割为若干个具有时变参数的质量-弹簧-阻尼器系统,各参数均随着电梯轿厢的运动而变化,建立运动方程时要考虑曳引钢丝绳的每一段离散质量,因此方程组的维数要增加很多,当钢丝绳分割的段数越多,模型就越真实,但计算量呈几何级数的增加。采用瑞利方法能量原则对曳引绳的质量进行处理。
1 动力学模型的建立
本文建立的曳引比为1:1的电梯机械系统7自由度动力学模型如图1所示。
图中:m1、J1、r1分别为曳引轮的质量、转动惯量和转动半径;m2、J2、r2分别为导向轮的质量、转动惯量和转动半径;m30为对重质量,m3x为对重侧补偿链的质量,m3为对重及对重侧补偿链的总质量;m40为轿架质量,m4x为轿架侧补偿链和随行电缆的质量,m4为轿架及轿架侧补偿链和随行电缆的总质量;m50为轿厢质量,m5x为载重质量,m5为轿厢及载重的总质量;kT、cT分别为曳引系统抗扭刚度、等效转动阻尼;k10、c10分别为曳引机底座橡胶及曳引机处承重梁的等效刚度、等效阻尼;k1t、c1t分别为曳引轮与导向轮之间的曳引绳的等效刚度、等效阻尼;k2、c2分别为导向轮处承重梁的等效弹簧刚度、等效阻尼;k3t、c3t分别为对重侧曳引绳的等效弹簧刚度、等效阻尼;k30、k40为绳头弹簧的弹簧刚度;c30、c40为绳头弹簧的等效阻尼;k4t、c4t分别为轿厢侧曳引绳的等效弹簧刚度、等效阻尼;k5、c5分别为轿厢底部减振橡胶的等效弹簧刚度、等效阻尼;x1~x5分别为m1~m5的振动线位移;φ1、φ2分别为曳引轮和导向轮的振动角位移。

图1 曳引电梯动力学模型
对于该系统,采用拉格朗日(Lagrange)方程建立其动力学方程,有:

式中,T、D和U分别为系统的动能、耗散函数和势能;qi和Qi分别为对应于第i个自由度的广义位移和广义外力。
系统的动能包括所有惯性元件的动能及曳引绳的动能,对于曳引绳的动能,下面采用瑞利法进行处理。轿厢侧曳引绳的静位移如图2所示,假设轿厢侧曳引绳的变形是均匀的。因此,在距离轿厢y处曳引绳的位移与速度分别为:


图2 轿厢侧曳引绳的静位移
在电梯运行过程中,轿厢侧曳引绳l1的动能为:

同理可得曳引轮与导向轮之间的曳引绳l2的动能为:
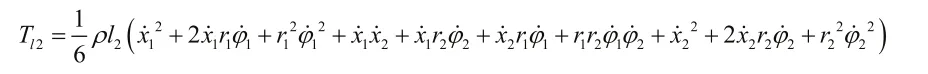
同理可得对重侧曳引绳l3的动能为:
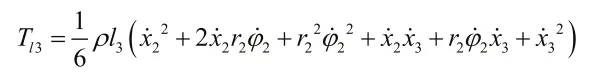
因此,系统的总动能T为:

系统的耗散函数D为:
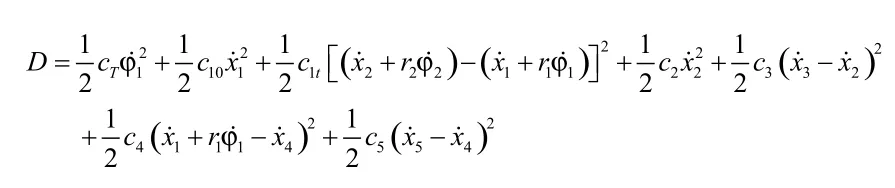
系统的总势能U为:
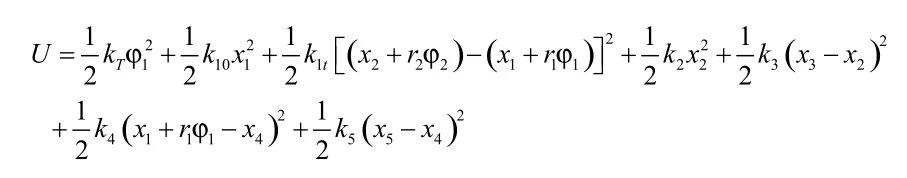
将上述结果代入方程(1)并整理成如下矩阵形式:
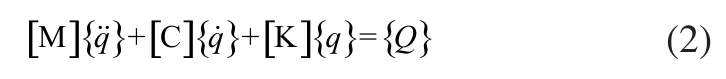
式中,[M]、[C]、[K]分别为系统的广义质量矩阵、广义阻尼矩阵和广义刚度矩阵;{}Q分别为系统的广义加速度、广义速度、广义位移及广义外力向量。其中,系统的广义位移向量为用求虚功的方法可求得系统非有势力的广义外力向量为系统的质量矩阵[M]、阻尼矩阵[C]和刚度矩阵[K]分别为:

式中,E、A分别为曳引绳的弹性模量、等效横截面积;l1为轿厢侧曳引绳的长度;l2为曳引轮与导向轮之间的曳引绳的长度;l3为对重侧曳引绳的长度。
2 动力学模型的求解
上述式(2)进一步转化为:
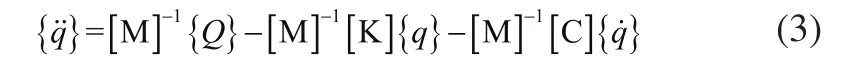
写成如下方程组的形式:

根据上式,可统一表示为:

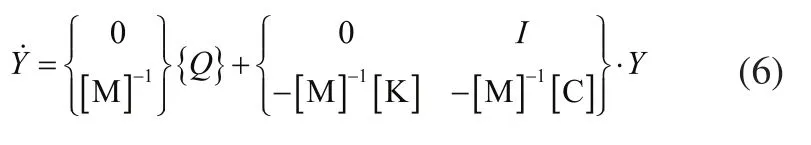
由上式,可通过数值方法计算广义坐标值Y,从而可确定轿厢的振动加速度和振动速度等。
3 实例仿真
下面本文以东南电梯股份有限公司生产的矿用电梯样机为例,求解该曳引电梯系统的动态响应。该电梯的配置参数如表1所示。

表1 矿用电梯样机配置参数
该电梯采用梯形速度曲线,轿厢的运动加速度如图3所示。
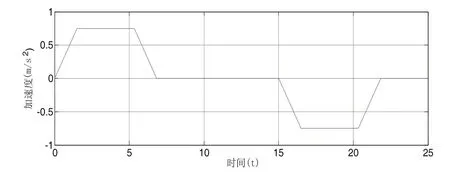
图3 轿厢的运动加速度
根据表1中的参数,采用Newmark-β法(ɣ=1/2, β=1/4)求解可得曳引电梯在空载上行时轿厢轿架及对重的振动加速度随行程的变化如图4所示。
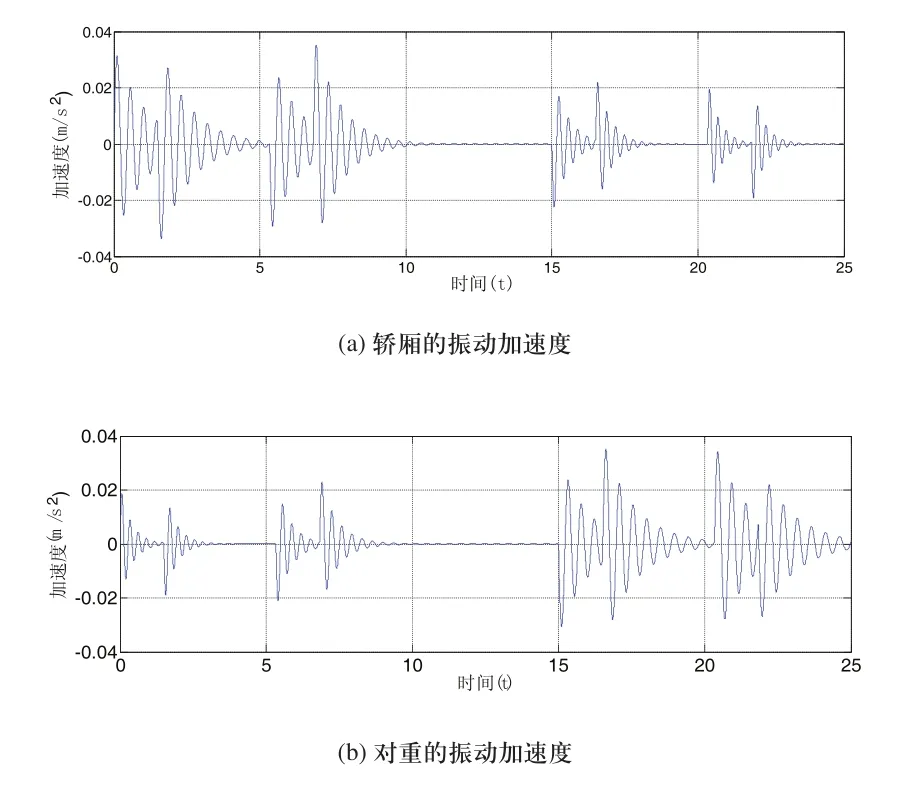
图4 轿厢上行时电梯系统的响应
由以上仿真结果,可以分析得到如下结论:
1)综合分析图3~图4,发现在轿厢运动加速度不光滑的时刻,振动加速度往往突然增大,在以后规划电梯加速度曲线时宜采用光滑的加速度曲线,如正弦曲线。
2)由图4可知,轿厢及对重的振动加速度在井道顶部时要比井道底部时小,这是由于在井道顶部时曳引绳的等效弹簧刚度比在底部时大,这也体现了电梯提升系统的时变特性。
4 结束语
本文采用瑞利法处理电梯曳引绳的质量,建立了曳引比为1:1的斜行电梯机械系统7自由度动力学模型,并阐述了曳引电梯系统动力学模型的求解方法,最后以矿用电梯样机为例运用MATLAB软件编程求得该电梯系统轿厢及对重振动加速度的变化规律,对于电梯系统的减振设计具有一定的参考价值。
[1] Nai K, Forsythe W and Glldall R M. Modeling and simulation of a lift system [C].International conference on control,1992,14(9): 56-60.
[2]张长友,朱昌明,吴广明.电梯系统垂直振动分析与抑制[J].振动与冲击, 2003(4):74-77.
[3]张长友,朱昌明.电梯系统动态固有频率计算方法及减振策略[J].系统仿真学报,2007(16):3856-3859.
[4]刘希花,任勇生,单淮波.电梯系统垂直振动动态特性研究[J].山东科技大学学报(自然科学版),2010(1):62-66.
[5]Roberts R.Control of high-rise/high-speed elevators.Proceeding of the 1998 American Control Conference (ACC 1998)[C].Philadelphia,1998:3440-3444.
[6]刚宪约.曳引电梯系统动态理论及动力学参数优化方法研究[D].杭州:浙江大学,2005.

