浅论方波激励下RC电路的响应
张 伟,叶雁群,邢 亮
(江南大学物联网工程学院电子工程系,江苏无锡214122)
在“电路理论”和“电子技术”等课程中,方波激励下的RC电路的响应是一个教学难点。以往的教学大部分以时域的推导为主,而且涉及到的暂态波形无法直接让学生观察到,学生对于不同参数导致不同的输出波形理解不够深刻[1-2]。针对上述问题,本文从时域和频域两个方面对RC电路进行了讨论,利用Multisim给出了方波激励下不同参数RC电路的输出仿真结果,并对结果进行了说明。
已知RC电路如图1(a)所示,假设输入信号ui为1 KHz的方波信号,周期为 2T,T=0.5 ms,波形如图1(b)所示。试分析当时间常数不同时,输出波形的特点。
在0<t<T时,可认为是直流电源的一阶零状态响应,根据微分方程或一阶电路的三要素法,可得
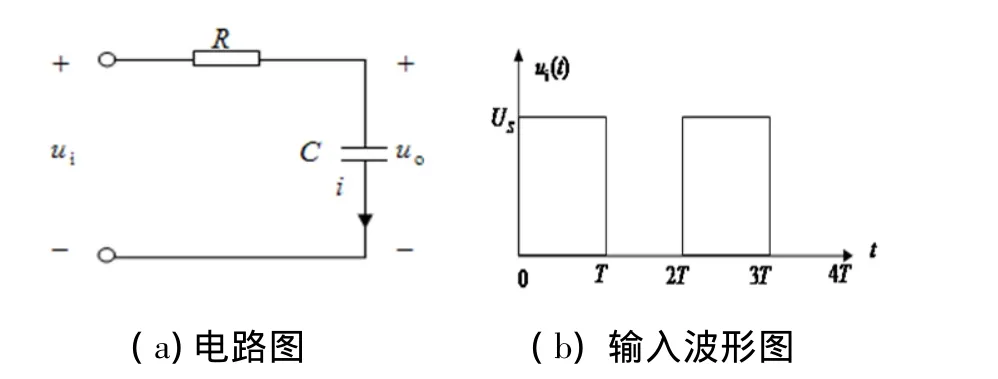
图1 一阶RC电路
1 一阶RC电路的时域分析

由式(1)可知,输出电压随时间从零开始按指数规律上升趋向于Us,在t=4τ时,输出电压与其稳态值相差1.8%,工程上一般可认为已经充电完毕。因此,τ越小,电容充电所用的时间越少。由于τ=RC≈T,可认为t=T(在第一个1/2周期)时,电容电压就已经达到稳态值,即uo=Us。
在T<t<2T区间可认为是外加激励为零的一阶RC电路的零输入响应。利用解微分方程或三要素法可求出输出电压为

在后面的周期过程中,重复上述充放电过程。
当 R=100 Ω,C=0.47 μF,τ =RC≈T/10 时,输出波形如图2(a)所示,充放电的过程呈现指数形式。因为时间常数比较小,所以过渡时间比较快,在1/2个周期内到达稳态。
当 R=100 Ω,C=470 μF,τ=RC≈T/10 时,输出波形如图2(b)所示。输入输出可近似为积分关系,所以输出波形为三角波[1]。这是因为时间常数很大,在指数函数的初期可以近似为线性波形。
当 R=100 Ω,C=470 μF,τ=RC≈T/10 时,输出波形如图2(c)所示。输出与输入波形基本相同,近似为方波。这是因为时间常数非常小,很快就达到稳态。所以过渡过程不容易观察出来。该电路在实际中得到广泛的运用,如在传输信号过程中,平行双线由于分布电容大,这些电容与平行双线的分布电阻可组成RC电路。因为时间常数比较长,若传输高频率的数字信号,容易失真。而双绞线的分布电容比较小,时间常数小,能够传输高速数字信号。

图2 时间常数不同时的电容电压输出波形图
当RC电路的输出为电阻电压时,不同RC取值对应的输出波形如图3所示。当τ=RC=2T时,波形如图3(a)所示,近似为方波。当τ=RC=20T/T时,波形如图3(b)所示,此时波形失真很小。当τ=RC=0.2T≈T时,波形如图3(c)所示。因为时间常数很小,输入输出可近似的认为是微分关系[1]。该电路可用于波形变换,可用作数字电路中的触发信号。该电路的分析与前述电路的分析类似,波形产生的原因亦可从时间常数的角度加以说明。

图3 时间常数不同时电阻电压输出波形图
2 一阶RC电路的频域分析
对于上述RC电路也可以从频域角度分析,方波信号可以展开成傅立叶级数:

从式中可以看出,一个方波含有基波成分和高次谐波,而其前后沿是否陡峭与所含高次谐波分量的多少有关,所含高次谐波愈多,其前后沿就越陡峭,信号的失真就越小。而一个方波的顶部是否平坦,和其所含低次谐波(主要是基波)有关。所以判断一个RC电路的输出波形可以从频域角度来分析。
图1所示电路的传递函数:
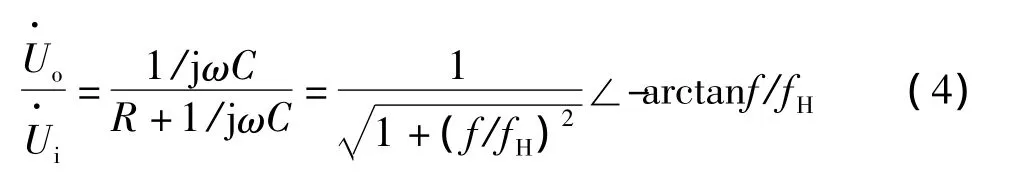
电路的幅频特性如图4(a)所示,该电路为低通电路。当RC时间常数τ由小变大时,fH值变小,高频特性变差。
当τ=RC/T时,因为fH=1/2πRC的值很小,电路的通频带较窄,方波中的高频分量被滤除了,其上升沿和下降沿由很陡变缓,即为电容C充电的指数函数的起始部分,成为近似的三角波。
而实际中,在分布参数的电路或放大器中,元器件和连接线之间(或与地之间)均存在较大的分布电容,这是电路或放大器的上限频率fH不能提高的一个重要原因。减小元件连接线之间的分布参数在电路设计、版图设计和安装调试中是一个重要课题。
当τ=RC≈T/10时,因为 fH==1/(2πRC)的值很大,电路的通频带较宽,能让方波中的高频分量通过,所以信号能不太失真的通过本电路。
若RC电路的输出为电阻的电压时,电路的幅频特性如图4(b)所示,该电路为高通电路。当RC时间常数由小变大时,fL值变小,低频特性变好。
当 R=100 Ω,C=10 μF,时间常数 τ=RC=2T时,因为fL的值比较低,方波中的低频分量仍然有一部分能通过,所以信号能不太失真地通过电路,输出近似为方波。
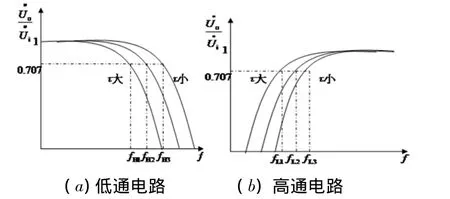
图4 RC电路幅频特性图
当电路的 R=100 Ω,C=100 μF,时间常数 τ =RC=20T/T时,因为fL的值很低,方波中的低频分量大部分都通过电路输出了,所以信号基本不失真,仍然为方波。
当 R=100 Ω,C=1 μF,时间常数 τ =RC=0.2T≈T时,因为fL的值比较高,方波中的基波及低次谐波分量被滤除了,所以方波的波顶迅速下降为0,而高频分量的上升沿、下降沿仍保持陡峭。此电路可以作为微分电路使用,将方波信号转换成正负尖顶脉冲输出,这一点在时域的分析中也有说明。可见,从频域和时域的角度分析得出的结果是一样的。
3 结语
RC电路在实际中具有广泛的应用。当R和C的参数不同时,电路所实现的功能也不同。本文从时域和频域两个方面对RC电路在方波激励下的响应进行了详细的讨论,给出了不同参数下输出波形的仿真结果,讨论了微分电路和积分电路应该满足的条件。利用Multisim软件,结果比较直观,大大方便了教学,加深了学生对基本概念的理解。
[1]秦曾煌.电工学(第七版)[M].北京:高等教育出版社2009,5.
[2]俎云霄,李巍海,张轶.应用Multisim进行无源RC电路的时频分析[J].南京:电气电子教学学报,2010,10:70 -71.
[3]张晖 Multisim在一阶RC电路响应中的应用[J].武汉:科教导刊,2012,27:106 -107.
[4]许树玲.一阶RC电路时间常数测量的难点及解决方案[J].吉林:大学物理实验,20l0,23(5):20 -21.
[5]孙景琪 孙京.电子技术3000问与答[M].北京:高等教育出版社,2013,9.
[6]李彩萍 方波激励下一阶RC电路响应的研究[J].天津:数字技术与应用,2011,11:107.
[7]洪正平 RC电路暂态过程的实验改进[J].济南:山东师范大学学报,2014,29(3):74 -75.
[8]James W.Nilsson Electric Circuits,(Ninth Edition)[M].北京:电子工业出版社,2012,2.

