高速铁路席位碎片化损益研究

文曙东，王富章，单杏花，卫铮铮

(中国铁道科学研究院 电子计算技术研究所，北京 100081)

高速铁路席位碎片化损益研究

文曙东，王富章，单杏花，卫铮铮

(中国铁道科学研究院 电子计算技术研究所，北京 100081)

高速铁路列车席位对号入座，由于需求的随机性，其席位裂解后发售会导致席位碎片化，出现多个不同号的席位可满足一个长区段旅客需求，在现实中却不能出售的情况，造成收益损失。通过随机过程模拟旅客订票，分析高铁席位碎片化程度。分析结果表明，席位碎片化造成的高铁收益损失不大。提出收益管理模式可以按顺序裂解席位的方案。

席位裂解；随机过程；席位碎片化

随着中国高速铁路（以下简称：高铁）的迅速发展，高铁的上座率越来越高。由于现在铁路客票的组织方法，高铁席位在裂解过程中[1]，逐渐碎片化，使得长区段的旅客买不到相应区段的票，而实际上列车在相应区段有闲置席位，只是碎片化在不同的席位号上 。

本文在目前的票务组织下，用随机理论模拟现有的席位发售过程，研究由于席位碎片化造成的收益损失，为铁路进行新一代客票系统的开发做前期研究。

1 席位碎片化

中国铁路执行收益管理模式，其中的存量控制方法采用嵌套式管理模式，不仅是不同价格等级之间的嵌套，还包含不同区段席位的嵌套，一个闲置席位可以面向若干区段出售[3～6]。收益管理不对席位库的闲置席位做事先预分，而按照需求依次裂解，这样会造成席位碎片化。

如图1所示，某线路有3个站，6个位置，1表示席位被占用，0表示席位闲置。现在每个席位都被碎片化了，如果来了1个AC区段的乘客，是不能满足该乘客的，而实际上，该线路上AB和BC区段各有3个闲置席位。铁路客运潜能没有发挥出来，这样收益得到了影响。

图1 席位碎片化示意图

2 高铁乘客需求过程模拟

做出如下假定：（1）不考虑取消订票。（2）拒绝一个需求会导致营运部门收入的损失。（3）每一个不同的始发站与终点站之间的需求用连续独立的随机变量表示。（4）假定每个区段的订票过程为泊松过程[7]。

假设（1）隐含了所有乘客购票后都将上车，不考虑（No-show）和超售（overbooking）的情况。假设（2）说明了被拒绝的乘客会流失到其它运输方式上，收益得到损失，不考虑被拒绝的乘客被其他车次挽回。假定（3）说明各个区段的需求是相互独立的，不考虑某些人故意买若干短程票来做长区段旅行。

观察某车次，如图2所示，共A、B、C、D、E等5个站点，所有区段需求总和为1 260个，如表1所示，其中，AB区段需求：均值λ=240的泊松过程；AC区段需求：均值λ=120的泊松过程。AD区段需求：均值λ=120的泊松过程；AE区段需求：均值λ=120的泊松过程。BC区段需求：均值λ=60的泊松过程；BD区段需求：均值λ=60的泊松过程。BE区段需求：均值λ=120的泊松过程；CD区段需求：均值λ=60的泊松过程。CE区段需求：均值λ=120的泊松过程；DE区段需求：均值λ=240的泊松过程。

图2 某高铁车次示意图

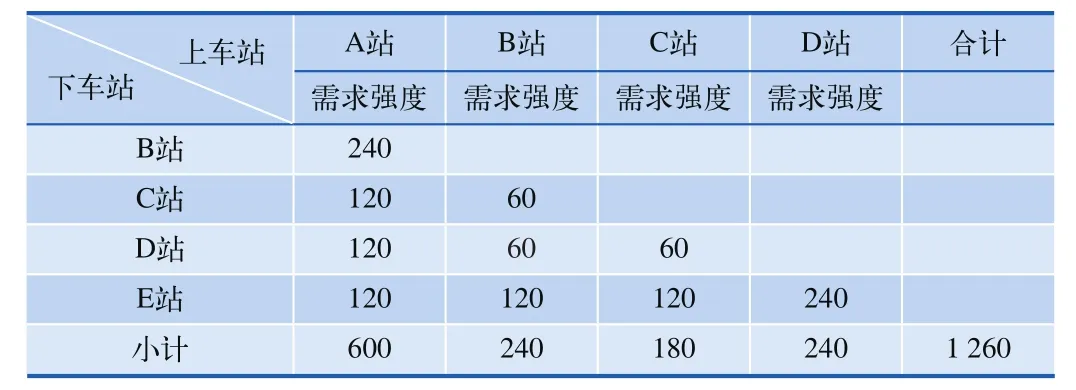
表1 各个区段需求强度表

席位总数为C=600个。如果每个区段的需求为期望值，那么每个区段席位都被占满，客座率为100%满员，如表2所示。但需求是随机的，每个区段的顾客不可能完全按照期望值到达，这样实际上客座率小于100%。

各个区段需求产生过程的模拟如下：

模拟本算例所有区段需求的期望值之和为1 260个，计算机产生1 260个随机数，表示1 260个需求。

当随机数为0＜α＜240/1260时，表示为AB区段需求，1 260个随机数落在该区间次数的期望值为240次，以此模拟AB区段需求期望值λ=240的泊松过程[8]。

当随机数240/1260＜α＜（120+240）/1260时，表示为AC区段需求，1 260个随机数落在该区间次数的期望值为120次，以此模拟AC区段需求期望值λ=120的泊松过程。

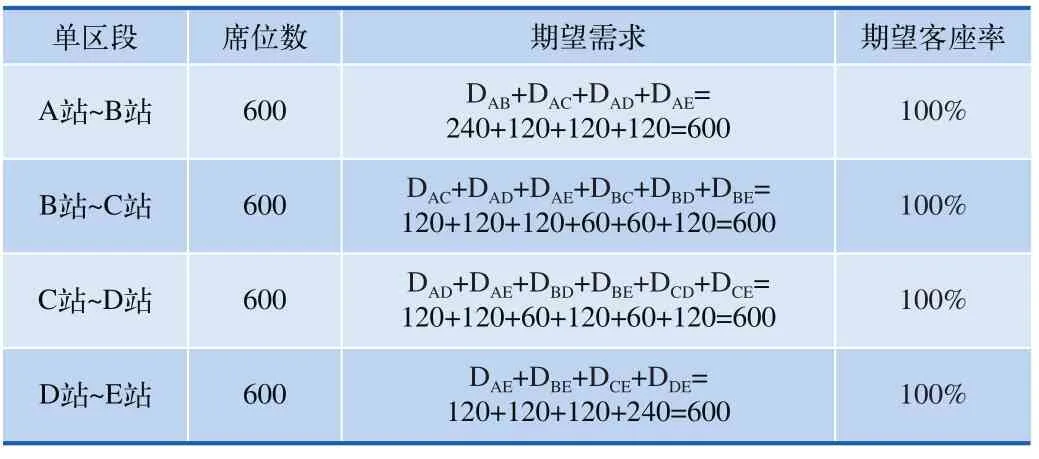
表2 各个单区段客座率

其他区段的需求以此类推。这样，产生一个随机数，就产生一个需求，至于该需求为哪个区段的需求，则看随机数的数值到底落在哪个区段。这样就模拟了1 260个需求，按照一定的概率分布在各个区段。本文指定了整趟列车的总需求为1 260个，按照一定的概率分布在各个区段，各个区段订票的先后顺序也是随机的，和旅客订票实际特征有些不吻合，但是拿来分析席位碎片化后对收益的影响，能够说明问题。

3 模拟列车完整订票过程

3.1 普通订票过程的模拟

列车席位编号为1、2、3、…、600，需求产生时，按照席位编号依次寻求可用席位，如果当前席位不能满足，则马上查看下一个编号的席位是否在相应区段闲置。如果可用，则出票。

用Status（600，4）表示600个席位在4个单区段是否被占用。如果Status（i，j）=0，表示第i个席位的第j区段位置空闲可以出售；如果Status（i，j）=1，表示第i个席位的第j区段位置已经被占用，不可出售。如果来了OD区段的预订需求，为其订票选席位的步骤如下：

第1步：从第1个席位查起，一次查到第i个席位。

第2步：查询i席位的（O，D-1）区段的是否被占用Status（i，O），Status（i，O+1），…，（i，D-1）。

第3步：对第2步中的Status求和。

如果∑Status=0，那么i席位在OD区段闲置，可以被占用出售，位置被选中，退出。

如果∑Status＞0，表示i席位在OD区段中至少一个单区段被占用，不可出售。回到第1步，继续查询下一个席位。

用Visual Basic 6.0编制程序如下：

For i= 1 To 600 依次查询600个席位

Sta = 0 表示席位OD区段闲置状态Status

For n = O To D – 1 O为起站、D为终站，查询OD区段中席位占用情况

Sta = Status(i, n) + Sta

Next n

if Sta =0 then exit for相应区段是否被占用，如果Sta累计为0，表示席位i可用

Next i

这样就模拟了列车的订票过程。本文建立完整的订票过程，下面模拟10次订票，查看有效订票数量以及拒绝次数。假定票价为Price（O，D）=（D-O）×100，那么10次订票结果如表3所示。

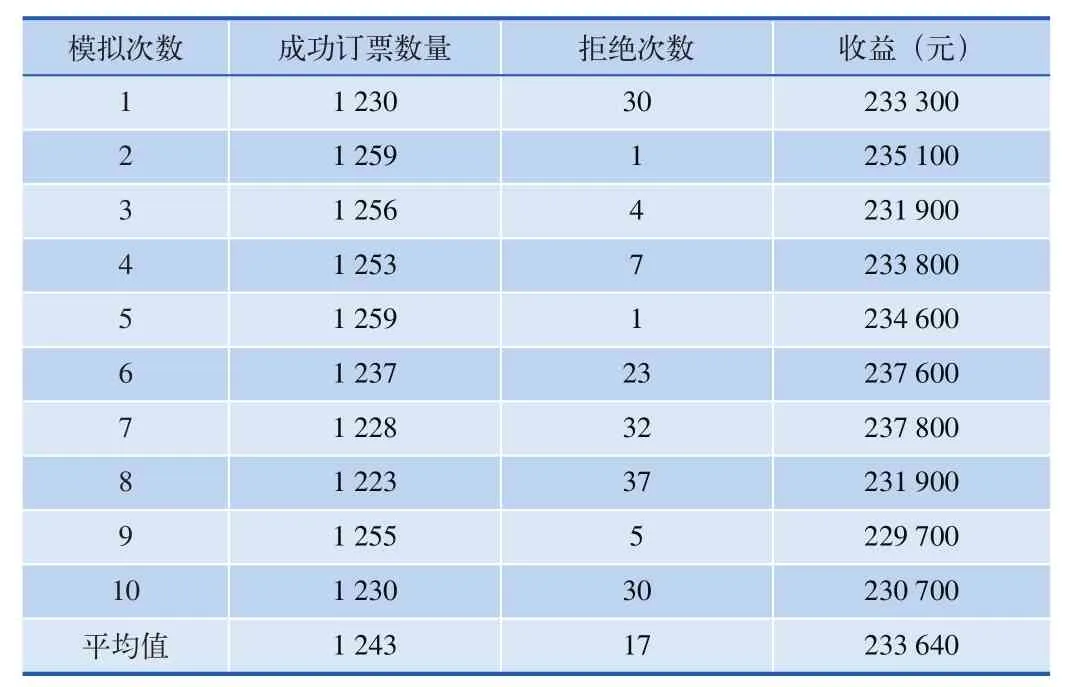
表3 普通订票过程模拟结果

可以看出，按照指定的需求强度，平均每趟车拒绝需求17次，平均收益233 640元。

3.2 碎片化席位整合出售订票过程的模拟

假定，如果AE需求来临时，没有AE可利用的空置席位，但有两个不同席位在AB、BE区段上分别闲置，那么就可以把这两个席位生成两张联席票，整合成一张票出售，乘客需要在B站换位置。如果OD区段来了一个预订需求，为其选座模拟步骤如下：

第1步：从第1个席位查起，一次查到第i个席位。

第2步：起点站为O1∈（O，D-1），终点站为D做循环，按照3.1小节中普通订票过程的模拟，查询第i个席位O1D区段是否空闲。

如果空闲，意味着O1D区段可以被占用，令D=O1，回到第1步，从第1个席位查起，继续查询OD区段是否闲置。

如果占用，回到第1步，继续查询i+1席位。

第3步：如果最后查到O=D，意味着找到了联程空闲席位。

查询第1个席位OD区段是否空闲：Do While D＞ O

For O1= O To D - 1

Call Chaxun按照3.1中的步骤查询O1D区段是否有闲置席位

If ∑Status=0 Then 如果席位空闲，令D=O1。

D = O1

Exit For

End if

Next O1

Loop

经过多次循环后，如果D=O，那么意味着列车有相应区段上的闲置位置，可以整合出售。本文建立完整的订票过程，碎片化席位可以整合出售，下面模拟10次订票，查看有效订票数量以及拒绝次数。同样假定票价为Price（O，D）=（D-O）×100，那么10次订票结果如表4所示。

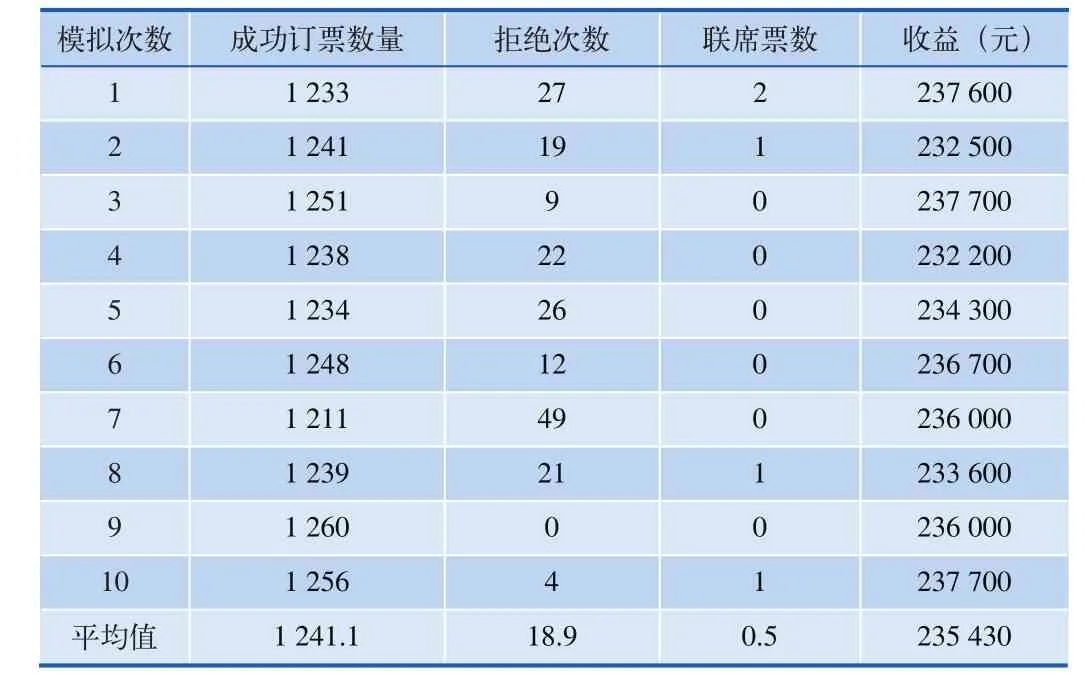
表4 碎片化席位可整合出售模拟结果

可以看出，按照指定的需求强度，平均每次拒绝需求18.9次，平均每次售出0.5张联席票，平均收益235 430元。

4 碎片化席位整合出售的效益

碎片化席位整合出售可以提高线路收益，平均每车次售出0.5张联席票。由于前面列举的样本数量为10，属于小样本数据。下面分别对上面两个订票过程模拟365次，观看一年的效果，如表5所示，结果显示平均每趟车有0.21张联席票，由于联席票相应位置如果不整合出售，还有机会出售给短区段，故收益仅增加0.1%。

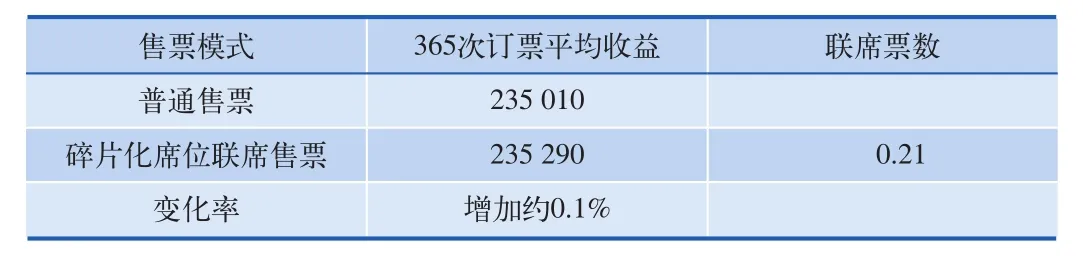
表5 两种订票管理方法订票结果比较表

本论文举例车次需求充足，期望客座率达到了100%，如此高的需求条件下，由于席位裂解碎片化造成的收益下降仅为0.1%，可以忽略。

5 结束语

目前高铁席位管理模式下，依次取出闲置席位去满足订票需求，在订票过程中，会出现席位碎片化的现象。由于乘客旅行中不能在中途更换位置，存在列车在相应区段上有闲置席位，而不能满足少量长距离顾客的需求情况。本论文通过产生随机数订票模拟了一个600席位车次的订票过程，需求预测值和席位数正好匹配，通过365次模拟结果显示，车次平均每次运行可能产生0.21次联席票，也就是说，如果执行联席售票，相比原有席位管理模式，可以多满足0.21个长距离的旅客需求，收益增加0.1%。

本文在需求的模拟中，整趟列车总需求每次模拟都定值为1 260个，并且需求随机到达，与实际订票过程有些偏差，但是可以观察席位碎片化对收益的影响。经过模拟计算分析，列车席位碎片化对收益的损失影响不大，按照席位依次裂解管理模式，在执行收益管理时，席位完全可以按照顺序裂解分配给订票者，而不用考虑席位碎片化的影响。

[1]单杏花，周亮瑾，吕晓艳，等. 铁路旅客列车票额智能预分研究[J]. 中国铁道科学，2011，32（6）：125-128.

[2] 张秀敏.我国铁路客票折扣销售研究[D].成都：西南交通大学，2005：75-76.

[3] Lee T. C., M. Hersh. A Model for Airline Seat Inventory Control with Multiple Seat Bookings[J]. Transportation Sci, 1993(27): 252-265.

[4]李金林，徐丽萍.运输网络中舱位控制模型与策略[J].交通运输工程学报，2009，9（1）：100-107.

[5]张秀敏，赵冬梅，文曙东.复杂运输网络存量控制研究[J].系统工程，2004，22（5）：7-11.

[6]单杏花.铁路客运收益管理模型及其应用研究[D].北京：中国铁道科学研究院，2012.

[7] Feng Youyi, Bai Chunxiao. Optimal Policies of Yield Management with Multiple Predetermined Prices[J]. Operations Research, 2000(48): 332-343.

[8] 于建梅.基于泊松分布的需求预测模型设计[J].物流科技，2010（5）：36-37.

责任编辑 陈 蓉

Project and loss of seat fragmentation for High-speed Railway

WEN Shudong, WANG Fuzhang, SHAN Xinghua, WEI Zhengzheng
( Institute of Computing Technologies, China Academy of Railway Sciences, Beijing 100081, China )

All seats were reserved seats in the train of High-speed Railway. Due to the stochastic demand, cracking seats would cause the seat fragmentation. There were several different number of seats which could meet a long section of passenger’s demand, on the contrary, these tickets couldn’t be sold in reality, and caused the loss of income. By the way of the simulation analysis for random process of passengers booking process, the degree of fragmentation for High-speed Railway seat was analyzed. The result showed that the loss of income wasn’t great due to fragmentation, and cracking seats in order was allowed during executing revenue management.

cracking seats; random process; seat fragmentation

U293.22∶TP39

A

1005-8451（2015）06-0005-04

2014-11-13

中国铁路总公司重大课题（2014X012）。

文曙东，在读博士后研究生；王富章，研究员。