戴维宁—诺顿定理的推广应用

梁永清，韦东梅，韦忠海

(广西大学电气工程学院，广西南宁530004)

等效电源定理(包括戴维宁和诺顿定理)是线性网络分析中的一个重要定理，也是“电路理论”课程教学的重点。任何一个线性含源二端网络，均可表示为电压源或电流源模型。传统的戴维宁和诺顿定理只限于单端口，而应用于多端口网络则较少。

本文主要讨论等效电源定理在多端口网络中的推广应用，又称之为广义戴维宁—诺顿定理。可作为“电路理论”课程教学的补充，目的是扩大学生知识面、提高其电路综合分析能力。

1 广义等效电源定理三种形式[1]

广义等效电源定理:任何线性有源多端口网络可等效为一个所有电源置零的无源网络与多个等效独立电源组合的线性模型。该模型与原网络对接入端口的任意负载贡献相同的电压和电流。

以两个端口的线性有源网络为例说明。如图1所示，Z1与Z2为端口负载。这里负载可以是短路或开路、有源或无源的。

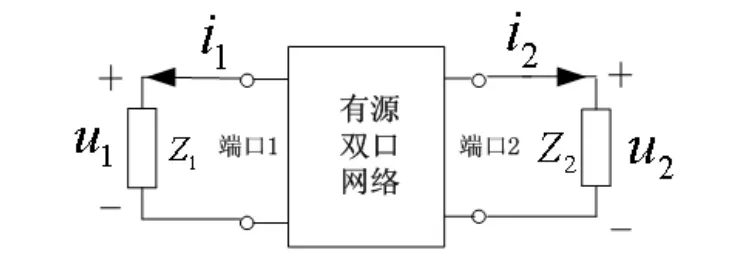
图1 线性有源双口网络

1)广义戴维宁-诺顿定理

2)广义戴维宁定理

设待求量为端口电流(i1、i2)，原网络可等效为图2(b)所示的广义戴维宁电路模型。E1和E2为端口开路电压。比较图1与图2(b)，对端口贡献相同的电流i1和i2。

3)广义诺顿定理

设待求量为端口电压(u1、u2)，原网络可等效为图2(c)所示为广义诺顿电路模型。J1和J2为端口短路电流。比较图1与图2(c)，对端口贡献相同的电压u1和 u2。

图2 广义等效电源定理求解模型

2 算例分析

[例1]电路如图3所示。设R1、R2为端口负载，i1、u1、i2、u2分别为待求量。试运用广义等效电源定理三种形式进行求解。

对于另一个代理变量APP的下载种类数量(新媒体使用广度)来说，它对于新生代女性农民工工作匹配的影响也存在一个适当的范围。APP的下载种类数量也必须控制在一定的区间范围之内才能对新生代女性农民工的工作匹配产生正向的影响。考虑到新生代女性农民工的群体特点，本文认为这里还有其特殊的原因。在实地调研访谈的过程中可以发现，新生代女性农民工对征婚交友类网站 APP 的使用普遍增多。这些征婚交友类网站APP的出现在一定程度上满足了新生代女性农民工对于婚恋交友的需求，但是这种APP下载种类数量的增多对其工作匹配并不会产生积极的影响作用。具体结果如表5所示：

图3 例1含独立电源电路

1)计算u1和i2

u1和i2为端口电压和电流，运用广义戴维宁—诺顿定理求解。

图4 广义戴维宁-诺顿电路求解模型

(1)选择端口:图3中R1为电压端口，将其短接;R2为电流端口，将其断开，如图4(a)所示。

(2)求开路电压E2和短路电流J1:由图4(a)，列KCL和KVL方程:ix+3=iy，1×ix+2iy=4A得ix=-(2/3)A，iy=(7/3)A，E2=2iy－2 ×1=(8/3)V，J1=2/2+ix=(1/3)A。

(3)构造广义戴维宁—诺顿电路:将原电路(图3)中有源网络电源置零(电压源短路、电流源开路)。端口反向接入J1和E2，得到图4(b)所示的广义戴维宁—诺顿定理等效电路，简化后得图4(c)。等效后对端口贡献相同的电流和电压，比较图3和图4(c)中u1和i2是相等的。

(4)根据简化电路计算u1和i2:由图4(c)解得u1=0.049 V，i2=0.73 A。

2)计算i1和i2

i1和i2均为端口电流，现运用广义戴维宁定理求解。

(1)选择端口:原电路图3中R1和R2为电流端口，将其断开，如图5(a)所示。

(2)求开路电压 E1和 E2:由图 5(a)，ix=

(3)构造广义戴维宁等效电路:将原电路(图3)中有源网络电源置零，端口反向接入E1和E2，如图5(b)所示。

(4)简化电路并计算i1和i2:图5(c)为广义戴维宁简化电路。由图解出结点电压un=0.3 V，i1=0.049 A，i2=0.73 A。

图5 广义戴维宁电路求解模型

3)计算u1和u2

u1和u2均为端口电压，现运用广义诺顿定理求解。

(1)选择端口:原电路图(3)中R1和R2为电压端口，将其短接得图6(a)。

(2)求短路电流J1和J2:由图6(a)，结点电压解出A。

(3)构造广义诺顿等效电路:将原图3中有源网络电源置零，端口反向接入J1和J2，如图6(b)所示。

(4)简化电路并计算u1和u2:图6(c)为广义诺顿简化电路。结点电压 uAO=1.46V，uBO=0.595V，uCO=0.546V;则 u1=uBO－ uCO=0.049V，u2=uAO=1.46V。

图6 广义诺顿电路求解模型

3 在含受控源电路中应用举例

对于含受控源电路，通常将受控源的控制量所在支路作为端口，将控制量作为待求量。构造广义等效电源电路。这样求开路电压和短路电流时就可将受控源消去，从而简化求解过程。

[例2]求解图7所示电路IA和UB

1)用广义戴维宁-诺顿定理求解

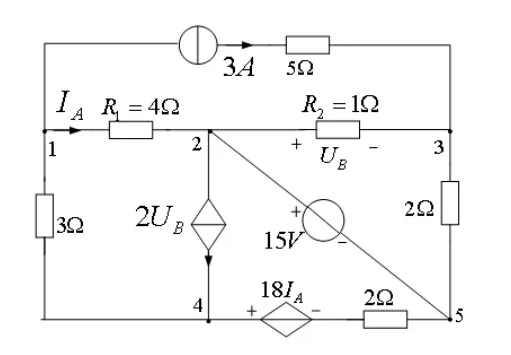
图7 例2含受控源电路

(1)选择端口:图7中R1与R2为端口负载，将R1断开，将R2短接。IA=0，UB=0两个受控源均为0，可将受控源消去，如图8(a)所示。

(2)求开路电压E1和短路电流J1:由图8(a)，E1+15+15=0得 E1=-30V，J2=15/2－3=(9/2)A。

(3)构造广义戴维宁—诺顿电路:将原电路(图7)中独立电源置零(受控源保留)。R1端口用反向E1替代，端口用反向J1替代，得到图8(b)等效电路。图中IA和UB即为所求。

(4)简化电路并计算IA和UB:由图8(b)列写+2(IA－6)=18IA，可解得 IA=2A。

图8 广义戴维宁-诺顿电路求解模型

2)用结点电压法验证

如图7，以5为参考点，列结点电压方程为

式中，控制量用结点电压表示:

IA=(u1－15/4);UB=15－u3

解方程得UB=3 V;IA=2A，结果与前一致。

4 结语

运用广义等效电源定理时，合理选择端口同时使方程有解是求解的关键。选择端口使有源网络唯一可解的充要条件是存在一个树，使得所有电压源(包括受控的)为树支，使得所有电流源(包括受控的)为连支。戴维宁端口的断裂形成应在独立连支处，而诺顿端口的并接形成应跨接独立树支[2]。本文将广义戴维宁-诺顿定理应用于多端口复杂电路的求解，通过算例分析，验证了该算法的正确性。实际运用时，广义等效电路应比原电路简单，通常不需列方程求解，只用KCL或KVL即可求解。

[1]梁永清，韦东梅，黄志强.应用广义等效电源定理求解含受控源电路[J]北京:大学物理，2014，7:30-34

[2]黄炳华.广义诺尔顿和戴维南定理的混合形式[J]北京:系统工程与电子技术1997，4:32-37

[3]胡钋.电路原理[M]北京:高等教育出版社，2011

[4]邱关源，电路[M]北京:高等教育出版社，2006

[5]邢丽冬.电路学习指导与习题精解(第二版)[M]北京:清华大学出版社，2008