改进的BP神经网络在高速铁路变形分析中的应用
胡震天,陈启华,李正通(南宁市勘察测绘地理信息院,广西南宁 530023)
改进的BP神经网络在高速铁路变形分析中的应用
胡震天∗,陈启华,李正通
(南宁市勘察测绘地理信息院,广西南宁 530023)
摘 要:将BP(back propagation)神经网络应用于高速铁路变形分析中,依据BP算法的特性,采用通过加入动量项的方法来提高BP算法的运算速度,并对此改进方法进行了实例论证。
关键词:高速铁路;变形分析;BP神经网络
1 引 言
由于我国地质结构比较复杂,作为长大线型的高速铁路,线下工程的沉降变形监测和分析显得极为重要。高速铁路线下工程沉降的安全监测、监测数据处理及变形分析,是确保施工及运营安全的重要保障,必须选择有效的监测手段和变形分析方法。神经网络所反映的函数关系不必用显式的函数表达式表示,而是通过调整网络本身的权值和阈值来适应,具有很强的非线性映射能力[1,2]。目前,BP神经网络研究已在大坝的变形分析应用方面取得了一定的成果,但同时我们还应看到,标准的BP神经网络仍具有训练速度慢的特点[3~5],本文对BP算法进行了改进,并将其运用到高速铁路变形分析中,并与改进前的BP算法进行了比较分析。
2 BP神经网络
BP网络是一个多层的单向传播的前向网络。网络除了输入和输出节点外,还存在隐层节点,而且在同层之间不存在耦合。工作信号从输入节点通过隐层节点传输到输出节点。每层节点的输出只受上一层节点的输入影响。隐层节点通常激活函数是Sigmoid型(f(x)= 1/ (1+exp(-Bx))(B〉0)),而输出输入节点有时也可以是线性的(f(x)= x)。
从输入到输出的BP神经网络是一个高度的非线性的映射,即F:Rn→Rm,F(X)= Y。对于样本集合:输入xi(∈Rn)和输出yi(∈Rm),可看作存在某一映射g 使:g(xi)= yii =1,2,…,n,现在要求出某映射f,使其在某种条件下(通常为最小二乘),f认为是g的最佳逼近。运用神经网络对简单的线性函数不断地复合,就可以逼近一些复杂的非线性函数。
BP网络包括输入层、隐层和输出层,各层之间都是相互连接的,如图1所示。
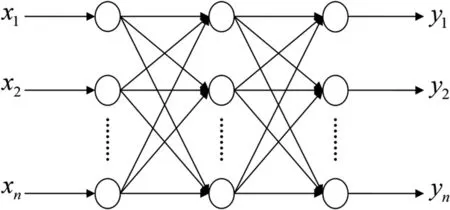
图1 BP网络结构
网络结构的设计没有可以遵循的固定的步骤,还要依靠经验来选取一定的参数,是一个综合性的问题。利用基于BP算法的神经网络解决一些实际问题,成功的关键取决于是否能提高网络的特性以及能否优化网络结构。对于三层的BP网络,初始权值的设置、激活函数的选择、隐含层节点数的确定,这些内容决定了其网络的结构。
3 BP神经网络的训练算法及改进
BP神经网络的训练学习过程由两个部分组成,分别是正向传播和误差反向传播。BP网络算法的一般步骤如下:
(1)选择网络输入,设置变量和参量;
(2)确定网络结构参数;
(3)对网络的连接权系数和神经元阈值的初值进行赋值;
(4)输入样本的评价模型和期望值;
(5)计算样本输出层和隐含层中各单元的实际输出值并计算方差Ei和E:对每一个输入模式i,其误差为:

系统总误差为:

其中dik为对应于第i个输入模式第k个输出层节点的期望值,yik为相应的网络输出值;
(6)若给定的收敛值E〈ε,则结束学习,否则调整权值让网络进一步学习,直到系统平均误差小于规定的要求为止;
(7)权值调整,使用递归从输出层开始逆向传播误差,直到第一隐含层为止,并用下式调整权值:
Wij(t+1)= Wij(t)+IrδjXi(3)
式中的Xi是第i节点的输出,IrδjXi是增益项,Wij为连接权值,δj为第j节点的误差,Ir为学习步长,t为迭代次数;
(8)转到(5)步;
(9)向学习好的网络输入要评价样本的评价因子。
BP算法虽然在大多数情况下可以得到满意的结果,但是仍存在一些不足,如:
①由于BP算法的本质其实是一个非线性优化问题,局部极小的问题会常常不可避免地出现,以至于得不到最优解;
②学习算法收敛速度慢;
③隐含层节点个数的选取缺少理论依据,学习训练时都是根据经验来选取;
④BP网络有时在学习新样本常常会忘了已学样本,同时也要求每个样本有相同的特征数目。
本文采用加入动量项算法对标准的BP神经网络模型进行改进:
由于BP神经网络在学习过程中,只需要改变权重,而权重和权重误差导数成正比。比例系数μ是学习过程的速率,它是一个常数。若我们能增大μ,则权重的改变也将加大,若能选择合适的速率,使μ的值尽可能大但又不至于引起振荡。这样就可以为系统提供一个最快的学习,增大学习率而又不导致振荡的方法,就是修改反传中的学习速率,使它包含一个动量项,具体地说,就是每个加权调节量加上一项正比于前次加权变化的量(即本次权重的修改表达式中引入前次加权的权重修改)。这就要求每次调节完成后,要把该调节量记住,以便在下面的加权调节中使用。带有动量项的加权调节公式为:

其中α为动量系数,一般取0.9左右。
引入动量项相当于在网络的学习过程中等效地改变了μ,μ不再是恒定的值。引入这个动量项后,使得调节向着底部的平均方向变化,不致产生大的摆动,即动量项起到缓冲平滑的作用。若系统进入误差函数面的平坦区,那么误差将变化很小。
4 实例分析
为了体现改进方法的优越性,现结合某高铁桥墩沉降变形监测数据来进行分析验证。现取桥墩变形监测网中的两个墩身观测标DK1252+590D2和DK1252 +614D1的20期数据进行分析,利用前15期观测数据序列作为训练样本,分别采用传统BP算法模型和对数据归一化后加入动量项的改进BP算法模型对后5期观测数据进行预测,如表1、表2所示。

DK1252+590D2沉降观测标的沉降量 表1

DK1252+614D1沉降观测标的沉降量 表2
传统BP算法和改进的BP算法预测结果:
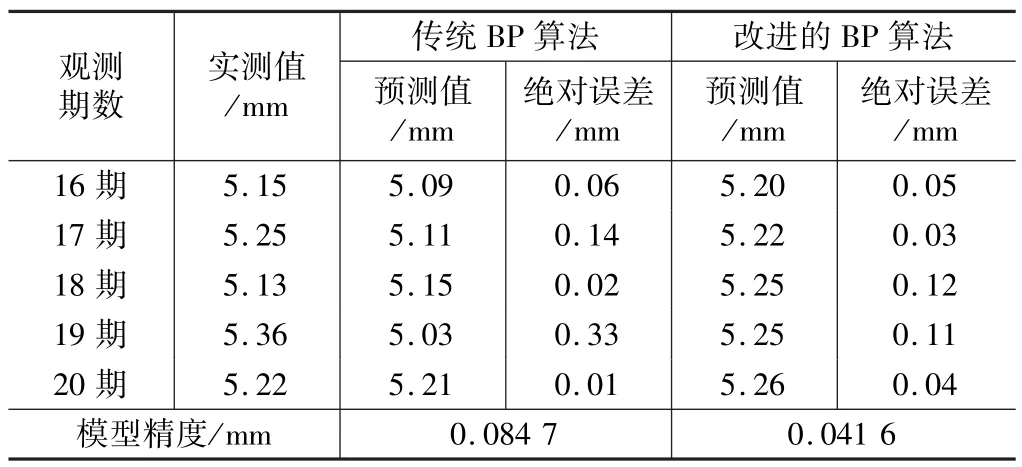
DK1252+590D2沉降观测标的沉降量预测结果 表3
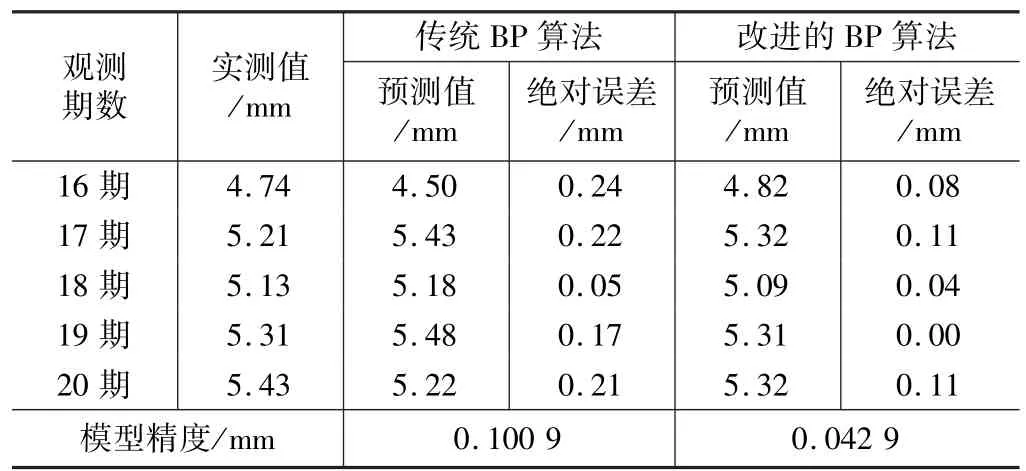
DK1252+614D1沉降观测标的沉降量预测结果 表4

图2 DK1252+590D2沉降观测标的沉降量预测结果比较图
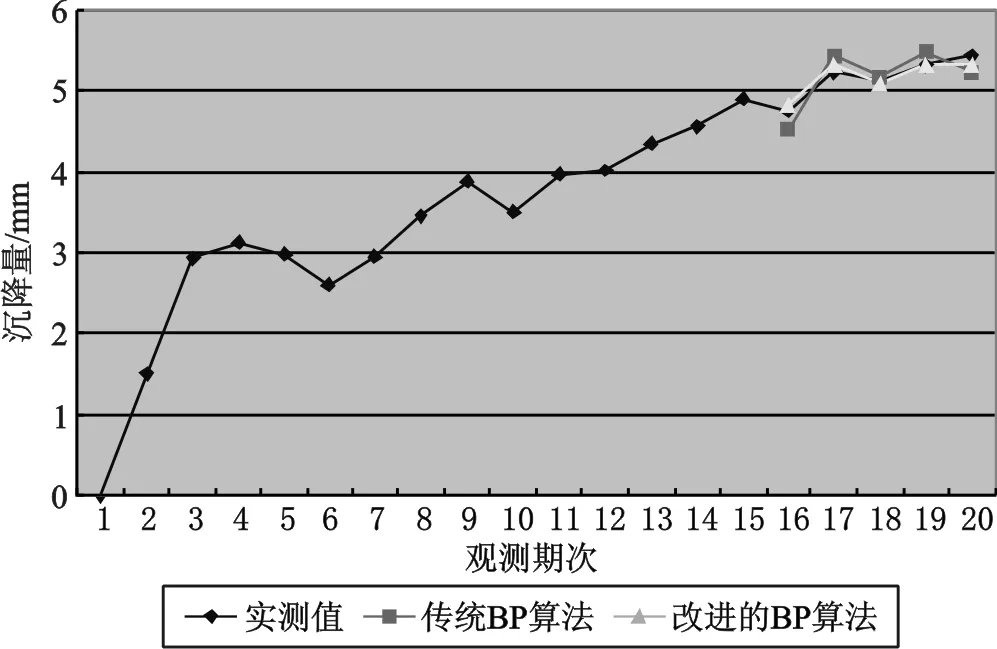
图3 DK1252+614D1沉降观测标的沉降量预测结果比较图
从表3和表4中的计算结果可以看出,改进的BP算法的绝对误差中小于0.1的比例比传统BP算法的大,由于对数据进行了归一化处理以及加入了动量项,使得改进后的算法精度更高,训练学习速度加快,并且使学习避免陷入局部最小。图2和图3说明了改进后的BP算法在沉降数据预测中的预测曲线比传统BP算法的预测曲线更符合实测值的曲线趋势,体现了改进算法的优势。
5 结 论
从实例可以得出改进的BP算法由于对数据进行了归一化处理以及加入了动量项,使得改进后的算法精度更高,训练学习速度加快,并且使学习避免陷入局部最小,说明改进的算法优于传统BP算法。
参考文献
[1] 袁曾任.人工神经元网络及其应用[M].北京:清华大学出版社,南宁:广西科学技术出版社,1999.
[2] 樊琨.基于人工神经网络的大坝位移预测[J].长江科学院院报,1998,15(5):45~48.
[3] 杨杰,吴中如,顾冲时.大坝变形监测的BP网络模型与预报研究[J].西安理工大学学报,2001,17(1):25~29.
[4] 吴秀娟.人工神经网络在大坝监测数据分析中的应用研究[D].武汉大学,2003.
[5] 胡上尉.多层前馈神经网络算法的改进及研究[D].重庆大学,2006:21~23.
[6] 周红晓,蔡俊,任德官.一种优化多层前馈神经网络中隐节点数的算法[J].浙江师范大学学报·自然科学版, 2002,25(3):268~271.
[7] 张正禄,黄全义,文鸿雁等.工程的变形监测分析与预报[M].北京:测绘出版社,2007.
[8] 乐红,余飞,韩卓等.武广铁路客运专线超载预压路基沉降评估技术[J].铁道标准设计,2010(2):11~14.
[9] 王新征,郑伟花.人工神经网络在预测软基沉降中的应用研究[J].路基工程,2010(1):128~130.
[10] 罗波,远祯.改进BP网络在深基坑变形预测中的应用[J].工业建筑,2006(S):79~81.
[11] 贺昌政,李晓峰,俞海.人工神经网络模型的新改进及其应用[J].数学的实践与认识,2002,7(4):554~561.
[12] 陈启华.小波神经网络在高速铁路变形监测中的应用[D].桂林理工大学,2012.
The Application of Improved BP Neural Network in the High-speed Railway Deformation Analysis
Hu Zhentian,Chen Qihua,Li Zhengtong
(Nanning Exploration & Survey Geoinformation Institute,Nanning 530023,China)
Abstract:In this paper,BP neural network can be used in the high-speed railway deformation analysis.Based on the character of BP algorithm,this dissertation uses a method to improve calculation speed of BP algorithm by adding a momentum and further prove this method by example analyze.
Key words:the high-speed railway;deformation analysis;BP neural network
文章编号:1672-8262(2015)04-145-03中图分类号:TU196+.1
文献标识码:B
收稿日期:∗2015—01—12
作者简介:胡震天(1983—),男,工程师,主要从事摄影测量与遥感生产、研发及技术管理工作。

