BDS/ GPS短基线的抗差方差分量估计及其应用

王建,陈现春,张献州(．国家测绘地理信息局第三大地测量队,四川成都 6000; ．西南交通大学地球科学与环境工程学院,四川成都 6003)

BDS/ GPS短基线的抗差方差分量估计及其应用

王建1∗,陈现春1,张献州2
(1．国家测绘地理信息局第三大地测量队,四川成都 610100; 2．西南交通大学地球科学与环境工程学院,四川成都 610031)

摘 要:BDS/ GPS组合观测值受观测环境的影响难免存在粗差或多路径等误差,基于最小二乘的方差分量估计不具有抵抗粗差或多路径等误差的能力,严重影响了随机模型的有效性。针对这一问题,基于抗差估计思想,引入双因子等价权函数,给出了抗差方差分量估计的实现过程。通过对BDS/ GPS短基线实测数据进行分析和计算,表明抗差方差分量估计可有效抵抗粗差或多路径等误差,提高了随机模型的可靠性,抗差估计成果具有更高的内符合精度。

关键词:BDS/ GPS；抗差估计；方差分量估计；双因子等价权

1　引 言

BDS作为中国独立发展、自主运行的卫星导航系统,现已具备区域导航能力,该系统在交通运输、城市勘测、水利水电、资源勘查等领域将发挥越来越大的作用。现阶段BDS星座呈现5GEO+5IGSO+4MEO的空间布局,中高纬度地区GEO高度角偏低,在城市、峡谷和山区进行测量时,受观测条件的遮挡和限制,有效观测卫星数较少,导致卫星定位结构较差,定位精度受到较大影响,此时BDS/ GPS组合定位将有利于改善GDOP值,提高定位结果的精度及其可靠性[1～3]。另外随着国际竞争的日益激烈和北斗事业的蓬勃发展,其推广应用具有重要战略意义,研究BDS/ GPS组合定位具有重要现实意义[3]。

短基线相对定位(≤15 km)常采用双差观测模型,针对不同观测精度的观测值采用方差分量估计定权[4],该方法无法抵御粗差或多路径等误差的影响,而抗差方差分量估计通过迭代计算的方式,基于观测值残差自适应地调整各类观测值的权比,定权方式更具合理性,抗差方法已在GPS网平差[5]、卫星精密定轨[6]以及单点定位[7]等取得了良好的效果。文中引入双因子等价权函数,建立抗差方差分量估计模型,对实测数据进行了计算,验证了上述方法的可靠性和有效性。

2　BDS/ GPS组合定位模型

2．1时空基准的统一

BDT和GPST都采用原子时系统,秒长定义一致,无闰秒问题[1,3]。BDT以协调世界时UTC(NTSC)为基准,起算历元为2006年1月1日零时零分零秒;GPST以美国海军天文台维护的协调世界时UTC(USNO)作为基准,起算历元为1980年1月6日零时零分零秒。因此BDT与GPST始终保持1 356周14 s的系统差。BDS坐标系统为CGCS 2000大地坐标系,参考于ITRF97,历元为2 000．0,而WGS-84坐标系与其在原点、尺度、定向及定向的定义都是相同的,仅扁率存在微小差异,该差异对于短距离的相对定位可以忽略[3]。

2．2组合定位观测方程

一般地,双差观测方程可表示为:λ▽△φjkAB=▽△ρjkAB-λ▽△NjkAB+▽△T-▽△I+ε(1)

式中,上标j、k为卫星,下标A、B为接收机;λ为载波相位波长;▽△φjkAB为相位双差观测值;▽△ρjkAB表示双差卫地距;▽△NjkAB为双差模糊度;▽△T为对流层残留误差;▽△I为电离层残留误差;ε表示其他误差和观测噪声。

采用式(1)解算模糊度时,卫星钟差和接收机钟差均被消除,对流层误差、电离层误差被大大削弱。为减小定位结果的系统性误差,此处仅在系统内组建双差观测方程,进而求得双差模糊度浮点解及其协方差阵,采用LAMBDA法[8]固定双差模糊度,实现BDS/ GPS短基线解算。

3　抗差方差分量估计

两类观测值的初始权可通过经验定权法确定,进而采用方差分量估计法定权。具体计算公式[4]如下:

上式中,下标G、C分别表示GPS、BDS系统;n为观测方程个数; tr (·)为求迹运算; T1 = N-1NG, T2=N-1NC;N为法方程系数阵;V为观测值改正数;P为观测值权;^σG和^σC为验后中误差。依据式(2)计算各类观测值的中误差,再依据式(3)重新定权直到各中误差相等为止。

式中,σ为任意常数,可取某类观测值(i=G、C)的中误差;k为迭代次数。

当观测值含有粗差或较大误差时,模型参数估值及方差分量估值会被扭曲,由式(2)计算验后中误差必然存在偏差。此时可采用抗差估计来减弱粗差或较大误差对方差分量估计的影响,确保随机模型的有效性。

考虑双差观测值间的相关性,引入双因子等价权函数[9]:

式中RiiRjj为自适应降权因子[9],可取为:

式中d=(k1-|^v|) / (k1-k0),^v=V/σV,k0可取1．5 ～2．0,k1取3．0～8．5。

采用双因子等价权可以保持观测值的相关性不变,且等价权矩阵严格对称。依据经验定权法计算的观测值改正数,结合式(5)计算等价权,并利用等价权替换式(2)的权矩阵,如此迭代计算直到各类观测值中误差相等为止。值得注意的是,迭代过程中式(2)的两类观测方程个数应为非零权的观测值个数。

4　实例计算

采用两个GNSS网的实测数据对本文方法进行了验证。第一个网为工程控制网,可实时观测7颗～10 颗BDS卫星和5颗～8颗GPS卫星,网中共有11个点,最长基线为10．1 km,平均基线长4．2 km;第二个网为变形监测网,可分别观测到5颗～6颗BDS卫星和GPS卫星,网中共6个点,最长基线为2．2 km,平均基线长0．9 km,其中有2个点受山体遮挡严重。现对不同时段的观测数据(采样率均为15 s)进行如下方案的计算:

方案1:基于方差分量估计的BDS/ GPS基线解算;

方案2:基于抗差方差分量估计的BDS/ GPS基线解算。

图1、图2为工程控制网采用以上两种方案计算的三边闭合环分量闭合差,图3、图4为变形监测网采用两种方案计算的三边闭合环分量闭合差。

图1　方案1的分量闭合差(工程控制网)

图2　方案2的分量闭合差(工程控制网)

图3　方案1的分量闭合差(变形监测网)

图4　方案2的分量闭合差(变形监测网)

由图1～图4可知,方案1的闭合环分量闭合差明显大于方案2的分量闭合差,这是因为受多路径等误差的影响,传统方差分量估计受到污染,导致方案1的基线解算精度偏低,而方案2具有抵抗粗差或较大误差的能力,基线解算结果具有更高的精度。现对以上数据分别进行单系统解算,闭合差信息如表1所示。

由表1知,工程控制网中,GPS解算和BDS解算的环闭合差精度相当,该网可观测的BDS卫星较GPS卫星多,提高了BDS单系统解算的精度;变形监测网中,GPS解算的环闭合差优于BDS解算的环闭合差,这说明在可观测卫星数相同且较少的条件下,BDS单系统不具有明显优势,这与BDS卫星独特的空间结构有很大的关系。另外,由于可观测卫星数的成倍增加,工程控制网的BDS/ GPS解算结果显著优于单系统解算结果,而变形监测网由于观测环境的限制,受多路径等误差的影响较大,方案1的解算结果精度提高并不显著,相反方案2的解算精度提高幅度较大。

环闭合差信息 表1

选取变形监测网中闭合环5的一条基线进行详细分析,图5给出了该基线部分双差观测值的残差分布,由图5可知双差观测值残差明显受到系统误差的影响。

图5　双差观测值残差序列图

现从第100个历元开始,每10个历元与前90个历元组成一个单元,共取20个单元数据进行单系统方案1和方案2的对比计算,并在第15个～20个单位的G01卫星和C03卫星L1观测值上分别加入0．4周的粗差。限于篇幅,图6～图9只显示了这20个计算单元的坐标分量与采用全部数据相对定位成果的偏差,均方根误差如表2所示。

图6　BDS解算的坐标分量偏差

图7　GPS解算的坐标分量偏差

图8　方案1的坐标分量偏差

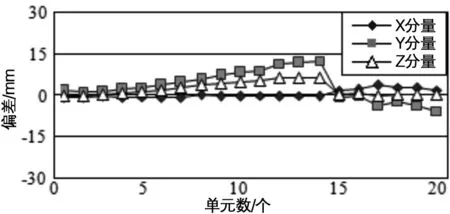
图9　方案2的坐标分量偏差

坐标分量偏差的均方根误差 表2

由图6、图7知,受卫星更替和卫星空间几何结构的限制,单系统解算的内符合精度并不理想,单系统解算的基线分量最大偏差大于3 cm,引入粗差后单系统解算结果呈现巨大的跳变。由图8、图9知,方案1的基线解算精度与单系统解算相比并无显著优势,而方案2的基线分量结果精度提高显著,人工添加粗差后方案1结果呈现跳变特性,而方案2抵抗粗差能力较强,解算结果呈现稳定特性。通过均方根误差的比较,抗差方差分量估计解算结果精度优于1 cm。

5　结 论

BDS/ GPS联合解算增加了卫星观测颗数,增强了卫星空间几何结构,显著提高了成果精度及其可靠性。通过闭合差统计和基线分量偏差的对比,采用抗差方差分量估计的解算方法有效抵抗了粗差或多路径等误差对定位结果的影响,提高了定位结果的稳定性和可靠性。针对受误差影响较大的变形监测数据,建议采用具有抗差估计思想的数据处理方法或软件,以便于获得准确可靠的变形信息。现阶段BDS/ GPS联合星座中存在四种不同类型的卫星,不同类型卫星的观测值精度不同,如何建立更为完善的随机模型,将是作者下一步的工作。

参考文献

[1] 杨元喜．北斗卫星导航系统的进展、贡献与挑战[J]．测绘学报,2010(1):1～6．

[2] 施闯,赵齐乐,李敏等．北斗卫星导航系统的精密定轨与定位研究[J]．中国科学:地球科学,2012,42(6):854～861．

[3] 高星伟,过静珺,程鹏飞等．基于时空系统统一的北斗与GPS融合定位[J]．测绘学报,2012,41(5):743～748．

[4] 崔希璋,於宗俦,陶本藻等．广义测量平差[M]．武汉:武汉大学出版社,2009:79～87．

[5] 刘长建,马高峰．抗差Helmert方差分量估计及其应用[J]．北京测绘,2002(1):16～22．

[6] 秦显平,杨元喜．抗差方差分量估计在卫星定轨中的应用[J]．大地测量与地球动力,2003,23(4):40～43．

[7] 蒋光伟,涂锐．抗差Helmert方差分量估计在精密单点定位中的应用[J]．测绘科学,2011,36(6):187～188．

[8] Teunissen P．The least-squares ambiguity decorrelation adjustment:a method for fast GPS integer ambiguity estimation [J]．Journal of Geodesy,1995,70:65～82．

[9] 杨元喜．自适应动态导航定位[M]．北京:测绘出版社, 2006．

Robust Variance Component Estimation and Its Application for BDS/ GPS Baseline

Wang Jian1,Chen Xianchun1,Zhang Xianzhou2
(1．Geodetic Third Team,National Administration of Surveying,Mapping and Geoinformation,Chengdu 610100,China; 2．Faculty of Geosciences and Environmental Engineering,Southwest Jiaotong University,Chengdu 610031,China)

Abstract:Variance component estimation is often used to determine the weighs of the observation values in combined BDS/ GPS positioning．The observations often have gross errors or large errors which have a serious impact on the effectiveness of stochastic model and distort the positioning result because of the variance component estimation based on least squares can’t resist gross error．To resolve this problem,a method which combines variance component estimation with the thoughts of robust estimation and implementation peocedures are introduced．The testing data indicates that robust variance component estimation can largely improve the robustness and reliability of combined BDS/ GPS positioning, and the results of combined positioning have a higher accuracy and more practical value．

Key words:BDS/ GPS;robust estimation;variance component estimation;equivalent weight

文章编号:1672-8262(2015)05-99-04中图分类号:P228,P207

文献标识码:A

收稿日期:∗2015—05—01

作者简介:王建(1985—),男,工程师,硕士,研究方向:GNSS数据处理与高精度变形监测。