不确定环境下机组调度问题的规划模型及算法

【摘要】传统航空公司机组调度模型大多是确定的，然而实际上航班通常会受各种不确定因素影响而产生延误的影响。本文考虑随机因素，将机组排班的配对寻优建成以成本最小和旅客满意度最大为目标的多目标随机机会约束规划模型，并构造混合智能算法来寻找最优解。案例研究的结果显示，模型和算法对于实际中机组配对的寻优是可行的。

【关键词】机组配对不确定多目标机会约束规划混合遗传算法

【Abstract】For the traditional airlines ， crew scheduling models are usually deterministic，in fact the flight is usually affected by many uncertain factors and cause delays. This paper take the uncertain factors into consideration to build a multi-objective stochastic chance constrained programming crew pairings model of minimum cost and maximum passenger satisfaction， and constructs a hybrid intelligent algorithm to find the optimal solution. the results of a case study show that the model and algorithm are feasible in practice for crew scheduling problems.

【Key words】crew pairings problems； uncertainty； multi-objective； chance constrained programming；hybrid intelligent algorithm

1 引言

由于民航业的特点和竞争的需要，航空公司的航班运行控制对运筹学的许多分支理论和方法，特别是最优化技术有着非常迫切的需求。航空公司计划和控制系统是围绕航班来运作的，运行控制部门通过使用辅助决策系统和利用各种现代优化技术建立符合实际问题的调度模型，采用有效的算法、软件来实现调度方案的快速生成。

在国内外的文献中，LOO[1]通过重新定义航班降落时间，建立一个用多目标遗传算法，（MOGA）来解决的多目标优化的模型。文献[2]则引入一个惩罚函数，模拟实际运营成本来进行不确定环境下的机组调度问题研究。张英楠等人[3]引入机会约束构建兼顾成本与航班运行安全及旅客随机需求的机型分配与机组排班模型。牟德一等人[4]提出机组延误概率这一概念，给出机组延误概率计算公式及方法，利用Matlab编程计算机组配对相关问题。Yen[5]一方面解决人员指派问题，另一方面加入惩罚函数来描述延误。文献[6]说明了确定性航班机组调度的综合论述。

本文在考虑基本的机组配对基础上，考虑实际运营情况，考虑一个不确定环境下的的随机变量。在航班约束以及机会成本约束条件下，建成多目标机会约束模型，利用混合智能算法求解并结合案例加以实现。

2 随机机会约束规划

定义[8]：假设x是一个决策向量，ξ是一个随机向量， 是目标函数， （j = 1，2，…，p）是没有给出确定可行集的随机约束函数。一个点x是可行的当且仅当事件 的概率测度不小于 ，即违反约束条件的概率小于 ，机会约束可以表示为如下的形式：

3 多目标规划

作为单目标规划的推广，多目标规划定义为在一组约束条件下，优化多个不同的目标函数，其一般形式为：

其中 是一个 维决策向量， 是目标函数， 是系统约束条件。

4 问题描述与基本方法

4.1 问题描述

机组调度的问题是航空公司制定航班计划表的一个重要组成部分。在机型分配结束后，为每个机型的飞机配备相应的机组人员来保证航班的飞行计划。为每个机型寻找合适正确的机组不仅能提高飞行效率节约成本，在飞行安全方面也有一定的保障。

机组调度问题分为两个部分：机组配对和机组轮班。机组配对是寻找适合的机组，机组轮班是配对以后，将具体的机组人员分配到配对中。在实际航空公司运营中，为一个机组配备相关的人员很容易操作，而机组配对的过程很复杂，涉及到机场、城市、基地等等限制规则，所以本文重点研究机组配对。

4.2 机组配对的一般要求

（1） 公司排班人员根据计划时刻表来对航班进行合理配对；

（2） 每个配对开始是从基地出发，结束则回到基地；

（3） 每个配对所安排的航班尽量能在一天内执行完毕以节省机组在外费用；

（4） 为机组人员分配合理的航线。

5 不确定环境下机组配对的机会约束多目标规划模型与算法

本文将航班进港时间设随机变量，将总成本和顾客满意度作为一个随机机会约束。

5.1 模型建立

5.1.1 符号约定

本文涉及的上、下标、参数、集合以及变量的实际意义，其中时间的计量单位是分钟，成本的计量单位是元。

上标和下标变量：

j = 配对下标变量；

i = 航班下标变量。

集合：

F：航班集合；

P：可行配对集合；

K：机组常驻基地集合；

参数：

：配对j航班i，旅客可容忍的进港时间窗；

：机组配对j的成本；

：常驻地城市可k用最少机组数量；

：常驻地城市可k用最多机组数量；

：航班i由配对j负责则为1；否则为0；

：配对j的常驻地基地是城市k则为1；否则为0.

决策变量

：如果配对j是解的一部分则为1；否则为0。

5.1.2 目标函数和约束条件

目标函数：航班晚点延误等的频繁发生会引起旅客满意度的下降。因此，综合航空公司飞行成本和旅客的满意度，本模型将航班总成本和顾客满意度作为目标函数。

由此，模型的目标函数可以写成下式：

本模型共有2组约束条件：

约束一：航班到港时间在旅客可接受的时间范围内。

航班计划的固定性与随机扰乱因素相互作用，导致了航班延误。在每个航班对每个航班中，我们希望旅客以置信度水平 在其可容忍的时间窗口内进港，于是机会约束为：

约束二：航班覆盖。

每个机组配对候选方案均覆盖了一定的航班数量，我们必须保证每个航班仅被覆盖一次。

例如，航班114在配对9、12、20和27中出现，因此要覆盖这个航班则有：

同理，所有航班i均可表达为上述形式。

5.1.3 不确定环境下机会约束规划模型

根据上节的分析，得到如下模型：

5.2 模型分析与混合智能算法

本模型是在基于整数规划中，加入了随机机会约束。模型有两个目标函数，模型混合智能算法的步骤如下：

步骤一：根据机组配对的规则和过滤条件得到所有的合法机组配对；

步骤二：根据航班起飞降落时刻、机型、乘客等等，确定模型参数和集合的取值范围；

步骤三：通过约束二确定航班的覆盖范围；

步骤四：利用混合智能算法来模拟输入输出数据，训练神经元等来实现约束一。

本模型的步骤三和步骤四的求解均由Matlab编程实现。

6 案例分析

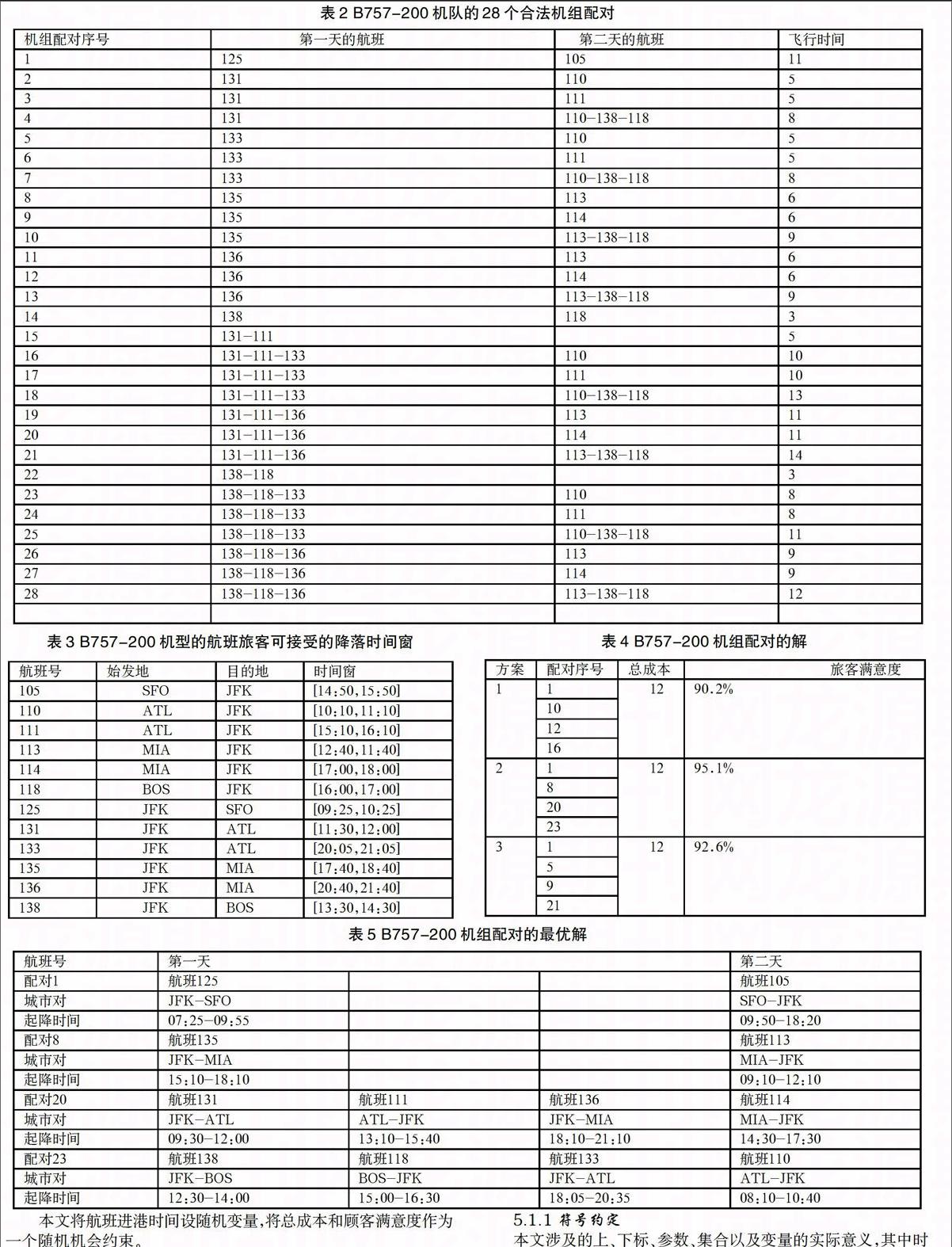
我们利用《航空公司运营规划与管理》书中B757-200机队的机组配对来进行案例分析。表一为该机型所有的航班调配。根据Ultimate Air公司对机组配对的要求（每个飞行出勤不能超过8小时；一个调配安排的最长时间为两天；机组的常驻基地是JFK机场；等待衔接时间的上下限分别为10分钟和3小时。），我们可以生成28合法机组配对，即表二。

表1 B757-200机型的航线调配

航班号 始发地 起飞时间 目的地 到达时间

105 SFO 09：50 JFK 15：20

110 ATL 08：10 JFK 10：40

111 ATL 13：10 JFK 15：40

113 MIA 09：10 JFK 12：10

114 MIA 14：30 JFK 17：30

118 BOS 15：00 JFK 16：30

125 JFK 07：25 SFO 09：55

131 JFK 09：30 ATL 12：00

133 JFK 18：05 ATL 20：35

135 JFK 15：10 MIA 18：10

136 JFK 18：10 MIA 21：10

138 JFK 12：30 BOS 14：00

表2 B757-200机队的28个合法机组配对

机组配对序号 第一天的航班 第二天的航班 飞行时间

1 125 105 11

2 131 110 5

3 131 111 5

4 131 110-138-118 8

5 133 110 5

6 133 111 5

7 133 110-138-118 8

8 135 113 6

9 135 114 6

10 135 113-138-118 9

11 136 113 6

12 136 114 6

13 136 113-138-118 9

14 138 118 3

15 131-111 5

16 131-111-133 110 10

17 131-111-133 111 10

18 131-111-133 110-138-118 13

19 131-111-136 113 11

20 131-111-136 114 11

21 131-111-136 113-138-118 14

22 138-118 3

23 138-118-133 110 8

24 138-118-133 111 8

25 138-118-133 110-138-118 11

26 138-118-136 113 9

27 138-118-136 114 9

28 138-118-136 113-138-118 12

航班延误是指航班降落时间比计划降落时间（航班时刻表上的时间）延迟30分钟以上或航班取消的情况。所以我们定义顾客可接受的进港时间窗为计划降落时间前后三十分钟，即表3。

表3 B757-200机型的航班旅客可接受的降落时间窗

航班号 始发地 目的地 时间窗

105 SFO JFK [14：50，15：50]

110 ATL JFK [10：10，11：10]

111 ATL JFK [15：10，16：10]

113 MIA JFK [12：40，11：40]

114 MIA JFK [17：00，18：00]

118 BOS JFK [16：00，17：00]

125 JFK SFO [09：25，10：25]

131 JFK ATL [11：30，12：00]

133 JFK ATL [20：05，21：05]

135 JFK MIA [17：40，18：40]

136 JFK MIA [20：40，21：40]

138 JFK BOS [13：30，14：30]

假设在旅客可接受的时间窗口内航班降落的置信水平为90%，即有机会约束：

同时，12航班全部覆盖且仅被覆盖一次，则有约束：

我们在上述两约束条件下极小化总成本，极大化顾客满意度。利用混合智能算法求解最优值。

算法步骤：

步骤1用随机模拟技术为机会约束不确定函数产生输入输出数据，

步骤2 根据产生的输入输出数据来训练一个神经元网络逼近不确定函数。

步骤3初始化pop_size个染色体，并利用训练好的神经元网络检验染色体的可行性。

步骤4通过交叉好变异操作更新染色体，并利用训练好的神经元网络计算所有染色体的目标值。

步骤5根据目标值计算每个染色体的适应度。

步骤6通过旋转赌轮选择染色体。

步骤7重复步骤4到步骤7直到完成给定的循环次数。

步骤8给出最好的染色体作为最优解。

首先利用随机模拟为不确定函数 产生输入输出函数，根据训练样本，我们训练一个神经元网络来逼近不确定函数 。然后，我们把训练好的神经元网络嵌入遗传算法产生混合智能算法。

通过运行混合智能算法，我们得到表4。

表4 B757-200机组配对的解

方案 配对序号 总成本 旅客满意度

1 1 12 90.2%

10

12

16

2 1 12 95.1%

8

20

23

3 1 12 92.6%

5

9

21

在总成本均为12的情况下，我们选择旅客满意度最高的方案2，即表5为最优解：

表5 B757-200机组配对的最优解

航班号 第一天 第二天

配对1 航班125 航班105

城市对 JFK-SFO SFO-JFK

起降时间 07：25-09：55 09：50-18：20

配对8 航班135 航班113

城市对 JFK-MIA MIA-JFK

起降时间 15：10-18：10 09：10-12：10

配对20 航班131 航班111 航班136 航班114

城市对 JFK-ATL ATL-JFK JFK-MIA MIA-JFK

起降时间 09：30-12：00 13：10-15：40 18：10-21：10 14：30-17：30

配对23 航班138 航班118 航班133 航班110

城市对 JFK-BOS BOS-JFK JFK-ATL ATL-JFK

起降时间 12：30-14：00 15：00-16：30 18：05-20：35 08：10-10：40

7 结语

本文是在不确定环境下，将机组排班的寻优建成以成本最小和旅客满意度最大为目标的多目标机会约束规划模型，并采用混合智能算法来寻找最优解。在保证最小成本下，使旅客在可接受的时间窗内降落机场。在航班所有可行机组配对后，利用Matlab编程求解，得到最优解。案例表明，该模型和算法对于实际中机组配对的寻优是可行的。

参考文献：

[1]Loo H.， Chul U.， A multi-objective genetic algorithm for robust flight scheduling using simulation [M]， ScienceDirect， 2007.

[2]Schaefer A J， Johnson E J， Kleywegt A J，et al.Airline crew scheduling under uncertainty [J].Transportation Science，2005，39（3）：210-223.

[3]张英楠，牟德一，李辉.基于机会约束规划的航班应急调度问题研究[J].中国安全科学学报，2012.

[4]牟德一，王志新，夏群.基于机组延误概率的鲁棒性机组配对问题[J].系统管理学报，2011，20（2）：207-212.

[5]Yen J， Birge J， A stochastic programing approach to the airline crew scheduling problem [D].University of Washington，2000.

[6]Barnhart， C. A. Cohn， E. L. Johnson， D. Klabjan， G. L. Nemhauser， P. H. Vance. Airline crew scheduling [M]. R. M. Hall， ed. Hand book in transportation Science， Kluwer Scientific Publishers， 2002：517-560.

[7]Charnes A， Cooper W. Chance-constrained programming [J].Management Science，1959，6（1）：73-79.

[8]刘宝碇，赵瑞清，王纲.不确定规划及应用[M].北京：清华大学出版社，2003.

[9]彭锦，刘保碇，不确定规划的研究现状及其发展前景[J].运筹于管理，2002，11（2）：1-10.

[10]杨立兴.不确定环境中的指派问题及其混合智能算法[D].保定：河北大学，2002.

[11]马苏德-巴扎尔甘（美）.航空公司运营规划与管理[M].邵龙，王美佳，译.北京：中国民航出版社，2006：39-56，81-91.

作者简介：张培（1994—），男，河南省商丘人，学历：本科。工作单位：中国民航大学。