影响弹簧扭转常数不确定度的因素分析
马书云
(解放军理工大学,江苏南京 211101)
螺旋弹簧的扭转常数与伸缩弹簧的劲度系数类似,是弹簧的基本属性之一。一般情况下,需要先通过实验测量出其值,然后作为常数应用在相应的实验中,而如何测量这一常数,以及影响测量的因素分析,目前研究甚少。基于大学物理实验中“扭摆法测量刚体的转动惯量”实验,分析影响螺旋弹簧的扭转常数测量的因素。有文献对影响该实验测量结果的因素进行了分析[1-3],分别从不确定度理论分析、光电门放置位置的影响等因素分析,而对放置不同标准件,对测量造成的不确定度影响还未有较深入研究,从螺旋弹簧扭转常数测量的不确定度传递公式出发,找出弹簧扭转常数测量的不确定度与不同标准件的质量、尺寸及周期测量之间的关系,提供减小不确定度的基本途径。
1 实验原理及方法
扭摆仪的核心部件是薄片状螺旋弹簧,将弹簧扭转视为简谐振动,周期为

其中,式中K为弹簧的扭转常数。
在实验中,首先测出载物空圆盘的转动周期T0,而后将标准件塑料圆柱、金属圆筒放置在载物圆盘上(标准件金属细杆直接与扭摆仪连接),测量转动周期为Ti,其转动惯量理论值Ji,根据几何形状计算得到,由式(1)得
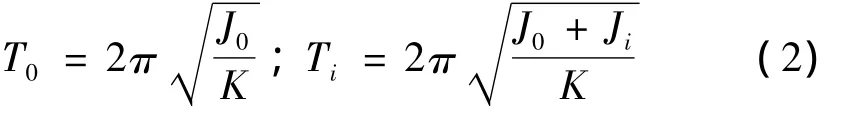
可以得到弹簧的扭转常数

2 不确定度传递公式的推导
扭摆法测弹簧扭转常数的实验中,弹簧扭转常数K是一个间接测量量,间接测量量的不确定度的传递公式如下[4]:

塑料圆柱、金属圆筒、金属细杆作为标准件进行实验,其转动惯量理论值为J1、J2、J3,测得弹簧扭转常数分别为K1,K2,K3,其转动惯量理论值和对应扭转常数分别为

可得到用塑料圆柱、金属圆筒和金属细杆这三种不同标准件测得的弹簧扭转常数的相对不确定度分别为

因为实验中使用同一周期测定仪测量转动周期,所以将由转动周期引起的不确定度简化为
可以看到,以上(8)(9)(10)三式中根号下的第一、二、三项分别是由标准件的质量测量、尺寸测量和周期测量引起的不确定度项,每一项不但与测量仪器的精度有关,还与标准件本身的质量、长度与直径有关。
3 影响不确定度因素的实例分析
3.1 实验基本数据
本实验分别用塑料圆柱、金属圆筒、金属细杆作为标准件,用精度为0.1 g的电子天平测量它们的质量,塑料圆柱直径、金属圆筒内外径用精度为0.02 mm的游标卡尺测量,金属细杆由毫米刻度尺(最小分度0.5 mm)测量,转动周期由精度为0.001 s的周期测定仪测量,表1给出了实验中的原始测量数据及由实验仪器造成的相应不确定度。

表1 标准件的质量、尺寸、转动周期及相应不确定度
3.2 影响因素分析
根据以上实验数据和不确定度的传递公式,计算得到弹簧扭转常数的相对不确定度,如表2所示。总相对不确定度由标准件的质量、尺寸和周期三项组成,分别简称为质量项a,尺寸项b和周期项d三项,c是由标准件的转动惯量理论值引起的相对不确定度项,c=a+b。

表2 用三种标准件测量弹簧扭转常数的相对不确定度
从表2数据可看出,以三种不同刚体作为标准件,测得的弹簧扭转常数的相对不确定度中,金属圆筒最小,为 0.17%,塑料圆柱最大,为0.28%,但相差不是太大。究其影响相对不确定度的因素可看出:
(1)转动惯量理论值测量因素的影响。
影响相对不确定度的两项为转动惯量理论值项c和周期项d,塑料圆柱与金属圆筒都是放置在载物盘上测量,尺寸测量与质量测量的方法及仪器相同,影响相对不确定度的主要因素是周期项d,而转动惯量理论值项c影响较小。而无需载物盘直接装在扭摆仪上测量的金属细杆,与前两者相反,主要影响因素是转动惯量理论值项c。
因此,应选择标准件的长度或直径较大,有利于降低不确定度,而测量标准件尺寸时,应选用精度较高的仪器。
(2)周期测量因素的影响
塑料圆柱与金属圆筒都是放置在载物盘上进行测量的刚体,影响扭转常数相对不确定度的主转动时的周期测量。金属圆筒与塑料圆柱的质量差别不大(分别为712.5 g,716.5 g),而金属圆筒的转动惯量较大,周期较长,引起相对不确定度的周期项 d较小,d1>d2。
因此,从周期项考虑,应选用精度较高的周期测定仪,在使用同种周期测定仪的情况下,应选择周期较大,即转动惯量较大的标准件,引起的相对不确定度较小。而金属细杆的周期测量时,没有塑料圆柱与金属圆筒。即使设T3=T1(或T2),载物盘的标准件的周期T1与空载物盘的周期T0不确定度越大,无载物盘的标准件(如金属细杆)转动周期T3越大,引起的相对不确定度越小。本实验中,金属细杆的周期项远小于塑料圆柱和金属圆筒。
可见,使周期项d减小,同样条件下,应选择不加载物盘的标准件,也更能减小测量的相对不确定度。
4 结 论
通过对相对不确定度公式的推导,从理论上得到了影响弹簧扭转常数测量不确定度的因素有测量仪器(包括周期测定仪、天平、游标卡尺等)本身的精度、标准件的质量m、尺寸D或L(直径或长度)、转动周期T以及是否有载物盘等。实验中塑料圆柱、金属圆筒及金属细杆三个标准件中,金属圆筒最小,为0.17%,塑料圆柱最大。
实例分析表明,有载物盘的标准件的不确定度主要由周期测量决定,而无载物盘的则主要由转动惯量理论值的测量决定;标准件的质量和尺寸(长度或直径)越大,越有利于减小相对不确定度;周期较大,即转动惯量较大的标准件,引起的相对不确定度较小;无载物盘的标准件(如金属细杆)转动周期越大,引起的相对不确定度越小;有载物盘的标准件的周期与空载物盘的周期相差较大时,弹簧扭转常数测量的相对不确定度较小。以上这些结论希望对实验中选择合适的标准件、减小实验测量的不确定度有一定帮助。
[1] 马亚林,陈建新.扭摆法测物体转动惯量的不确定度分析[J].大学物理实验,2011,24(1):78-80.
[2] 王丽香,张兵 扭摆法转动惯量测试仪中弹簧扭转常数的测定[C].全国高等学校物理基础课程教育学术研讨会论文集,2009,317-319.
[3] 邹红玉,郑红平.扭摆法测量转动惯量实验中光电门摆放位置的探究[J].物理实验,2009,29(1).
[4] 白忠,李延标,林上金.大学物理实验[M].北京:高等教育出版社,2012:11-20.

