水平油井IPR方程的建立与对比

陈元千 周 翠

（中国石油勘探开发研究院 北京 100083）

水平油井IPR方程的建立与对比

陈元千 周 翠

（中国石油勘探开发研究院 北京 100083）

油藏；水平油井；无因次IPR方程；产能预测

由于水平油井产能远比垂直油井高，因此在国内外油气田开发中得到了广泛应用。IPR方程是描述油井动态、预测绝对无阻流量和建立IPR曲线的重要方法。对于水平油井的IPR方程，到目前为止，仅有针对溶解气驱条件，利用油藏数值模拟研究结果，经统计建立的Bendakhlia ＆Azis［1］和Cheng［2］这2个经验方程。由于国外IPR方程的建立是以溶解气驱为基础，因而当井底流压明显降低时，所预测的产量偏低。本文引用文献［3］提出的等效驱动半径的概念和方法，将水平油井转成产量相等、形式相同的垂直油井，并利用垂直油井的研究方法，建立了预测水平油井绝对无阻流量和IPR曲线的IPR方程。通过实例应用，同国外的2个IPR经验方程进行了对比，得到了比较一致的预测结果。

1 水平油井IPR方程的建立与对比

对于稳定生产的垂直油井，当存在高速湍流（非达西流）影响时，不同渗流半径处的压力梯度与流动速度的关系可用如下Forcheimer（1901）的方程表示：

Green等［4］和Cornell等［5］的研究表明，式（1）中的常数a和b可分别表示为

将式（2）、（3）代入式（1）可得

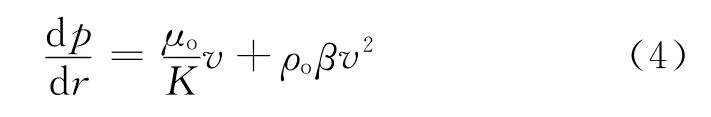
在稳定产量的平面径向流条件下，通过不同渗流半径截面的流动速度可表示为

将式（5）代入式（4）进行分离变量可得

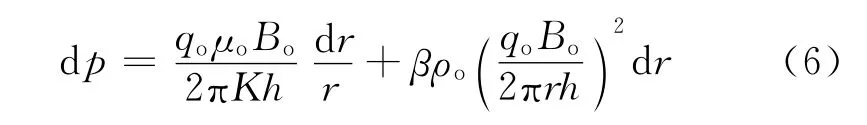
对式（6）代入上下限进行积分

引入文献［3］提出的等效驱动半径red的概念和方法后，可将水平井转为产量相等、形式相同的垂直井，Joshi［6］和陈氏［7］的水平井产量公式的等效驱动半径分别为式（8）和式（10）。

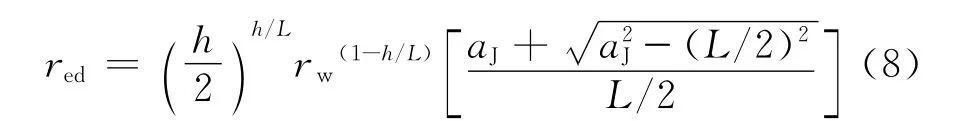
其中

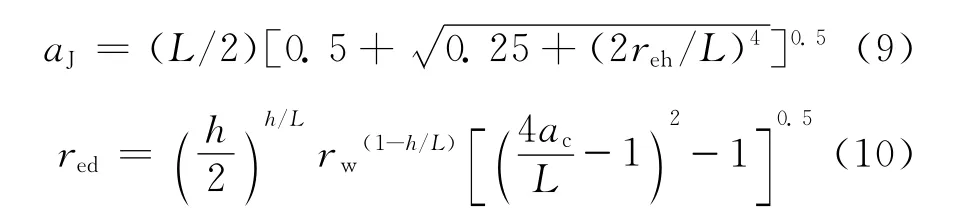
其中

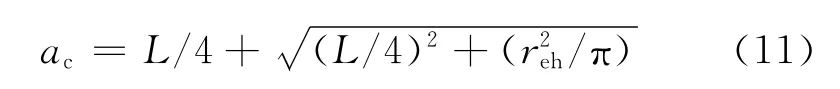
将等效驱动半径作为积分上限，由式（7）积分得

应当指出，上面公式推导所用的参数均为SI制基础单位，当改为矿场实用单位时（见符号说明），则式（12）表示为

由式（13）可得水平油井二项式的简单表达式为

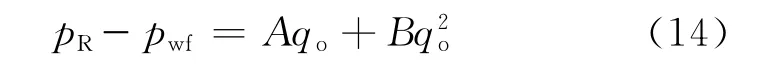
其中

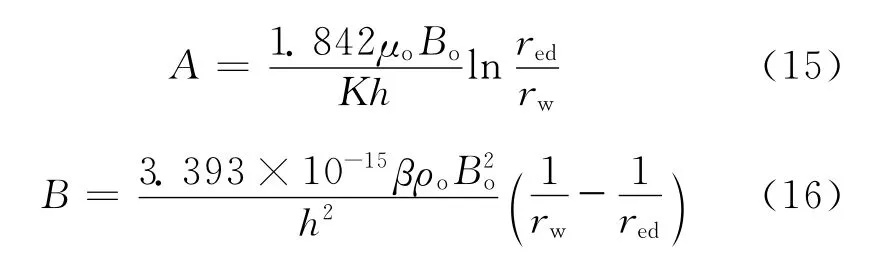
当由稳定试井取得水平油井多点（一般为4点）测试数据时，可由式（17）经线性回归确定A和B的数值，即

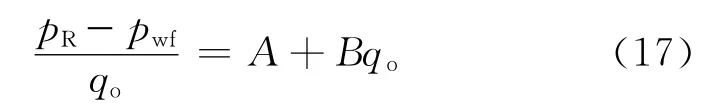
当已确定A和B的数值后，由下式确定水平油井的绝对无阻流量：

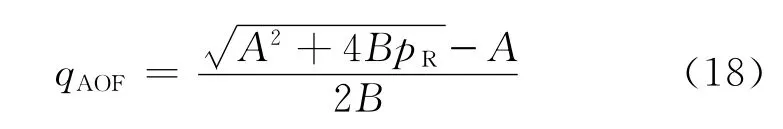
为了建立水平油井的IPR方程，将式（14）等号两端同时除以pR得

再将式（19）等号右端的第2项和第3项同时乘和除以绝对无阻流量qAOF，可以得到水平油井无因次IPR方程为

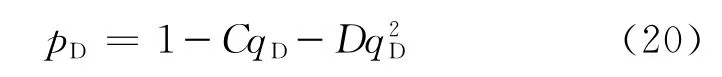
其中

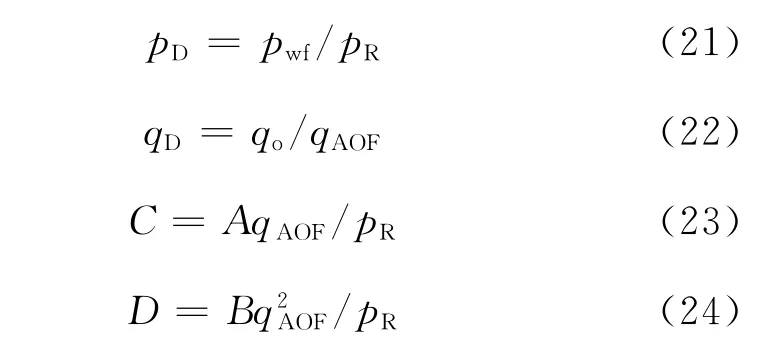
当pwf＝0时，pD＝0、qo＝qAOF、qD＝1，因此，由式（20）可得

再将式（25）代入式（20）得

式（26）是一个一元二次方程，求解后得

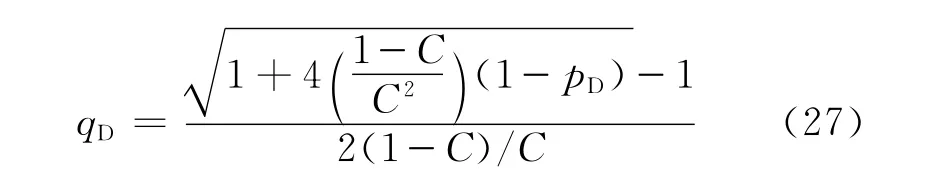
将式（21）和式（22）代入式（27），得到利用单点测试资料预测水平油井绝对无阻流量的关系式为

式（26）中的C可称为流态系数。当C＝1时，储层中流体的流动完全受层流控制；当C＝0时，储层中流体的流动完全受湍流控制。不同C值的无因次IPR曲线绘于图1，其中45°对角线为C＝1时完全受层流控制的直线。对于水平油井的C值，可通过多点测试资料，先由式（17）的线性回归确定A和B的数值，再由式（18）确定qAOF的数值，最后由式（23）确定C的数值。由于水平井的渗流阻力和湍流影响均比垂直井小，因而它的C值要明显的大于垂直井。

图1 不同C值的无因次IPR曲线Fig.1 Dimensionless IPR curves under different Cvalues

文献［8－10］的统计研究表明，对于垂直油气井，取C＝0.25可以得到比较满意的预测结果。对于水平油气井，若C值取为0.5，则由式（28）可得预测水平油井绝对无阻流量的关系式为

在已知pR的数值和由式（29）求得qAOF数值之后，再由式（30）预测不同pwf下的qo值，并用于建立水平油井的IPR曲线

Bendakhlia ＆Azis［1］利用油藏数值模拟技术获得了大量数据，对溶解气驱的水平油井提出了如下的IPR方程：

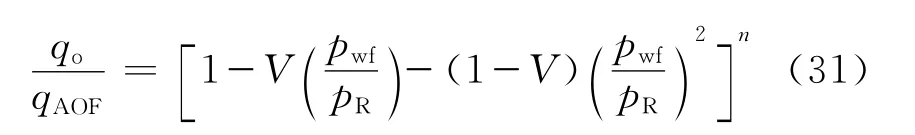
式（31）中：V为Vogel常数，n为Fetkovich指数，两者与油藏的地质采出程度有关。在文献［6］的应用时，取n＝1和V＝0.1得

Cheng［2，11］对溶解气驱的水平油井，同样基于油藏数值模拟技术获取的数据，参照Vogel的IPR方程形式，建立了如下的IPR方程：

2 实例应用

据文献［11］，某一水平油井的水平井段长度L＝305 m，地层压力pR＝16.650 MPa，pwf＝8.563 MPa和qo＝120.8 m3/d。试用本文方法、Bendakhlia ＆Azis法和Cheng法，预测该水平油井的qAOF和IPR曲线。在已知qAOF和pR数值的条件下，给定不同的pwf值，分别求得3种方法的IPR曲线，见图2。

由图2看出，在pwf＞6 MPa之前，3种方法的预测结果非常一致；但在pwf＜6 MPa之后，Bendakhlia ＆Azis法和Cheng法的预测结果明显比本文方法偏低，这可能与Bendakhlia ＆Azis法和Cheng法是溶解气驱条件有关，因为在pwf＜6 MPa之后，近井地带油层内脱气严重，气相渗透率大幅增加导致产量下降。

图2 3种IPR曲线的对比Fig.2 Comparison of 3types of IPR curves

3 结论

1）本文利用文献［3］提出的等效驱动概念和方法，将水平井转成产量相等、形式相同的垂直井，这样就可以利用垂直井的平面径向渗流理论，对水平油井的二项式进行推导，进而建立水平油井的IPR方程。该IPR方程可用于单点测试得到的pR、pwf和qo数据，预测水平油井的绝对无阻流量qAOF和建立IPR曲线。本文提出的IPR方程与Bendakhlia＆Azis和Cheng提出的2个IPR经验方程形式相似，但函数关系相反，更具有理论基础。

2）本文IPR方程中的C系数和Bendakhlia ＆Azis IPR方程中的V系数都存在一个合理选择的问题。本文提出了利用水平油井多点测试资料确定C值的方法，而由文献［8－10］的研究和应用表明，垂直油气井的C值取为0.25时可以得到比较好的预测结果。由于水平油井的渗流阻力和湍流的影响均比垂直井小，因此表示流态的C值要比垂直井大。当水平油气井的C值取0.5时，实例应用得到了与国外2种方法比较一致的预测结果。而在pwf＜6 MPa之后，国内2种方法的预测结果明显比本文方法偏低，这主要与溶解气驱井底流动压力降低引起近井地带脱气加剧的影响有关。

3）在3种水平油井IPR方程的应用对比时，本文方法水平油井的C＝0.5，但由式（23）可以看出，C值与A值成正比，与pR值成反比；再由式（15）可以看出，A值与流动系数（Kh/μo）成正比。因此，不同地区在应用本文的IPR方程时，可以对C值做出适当的微调。

符号说明

（括号内为SI制基础单位）

qo—水平油井的产量，m3/d（m3/s）；

qAOF—水平油井的绝对无阻流量，m3/d（m3/s）；

qD—无因次产量；

v—渗流速度，m/d（m/s）；

p—径向半径r处的压力，MPa（Pa）；

pR—地层压力，MPa（Pa）；

pwf—井底流压，MPa（Pa）；

pD—无因次压力；

Bo—地层原油体积系数；

μo—地层原油粘度，mPa·s（Pa·s）；

ρo—地层原油密度，g/cm3（kg/m3）；

K—有效渗透率，mD（m2）；

h—有效厚度，m（m）；

β—高速湍流系数，m－1（m－1）；

C—达西流动常数；

D—湍流流动常数；

r—平面径向流的径向半径，m（m）；

re—垂直油井的驱动半径，m（m）；

red—水平油井的等效驱动半径，m（m）；

reh—水平油井的拟圆形驱动半径，m（m）；

rw—水平油井的井底半径，m（m）；

A和B—二项式直线的截距和斜率；

a和b—Forcheimer方程的层流系数和高速湍流系数；

aJ—Joshi水平井产量公式椭圆形驱动面积长轴的半长，m（m）；

ac—陈氏水平井产量公式椭圆形驱动面积长轴的半长，m（m）；

L—水平井段长度，m（m）。

［1］BENDAKHLIA H，AZIS K.Inflow performance relationship for solution gas drive horizontal wells［C］.SPE19823，1989.

［2］CHENG A M.Inflow performance relationship for solutiongas－drive slanted/horizontal wells.SPE20720，1990.

［3］陈元千.确定水平井产能比、流动阻力比、驱动面积比和表皮因子的新方法［J］.中国海上油气，2009，21（3）：165－168.

Chen Yuanqian.New methods of determining productivity ratio，flow resistance ratio，drainage area ratio and skinfactor of horizontal well［J］.China Offshore Oil and Gas，2009，21（3）：165－168.

［4］GREEN L，DUWEZ P.Fluid flow through porous material［J］.Appl.Mech.March，1951，18：39.

［5］CORNELL D，KATZ D L.Flow of gases through consolidated porous media［J］.Ind.and Eng.Chem，1953，45：2145.

［6］JOSHI S D.Horizontal well technology［M］.Tulsa，Oklahoma：Pennwell Publishing Company，1991：240－243.

［7］陈元千.水平井产量公式的推导与对比［J］.新疆石油地质，2008，29（1）：68－71.

Chen Yuanqian.Derivation and correlation of production rate formula for horizontal well［J］.Xinjiang Petroleum Geology，2008，29（1）：68－71.

［8］陈元千.确定气井绝对无阻流量的简单方法［J］.天然气工业，1987，7（1）：59－63.

Chen Yuanqian.A simple method for determining absolute open flow rate of gas well［J］.Natural Gas Industry，1987，7（1）：59－63.

［9］陈元千.气井新的无因次IPR方程与应用［J］.油气井测试，1998，7（4）：22－26.

Chen Yuanqian.A new dimensionless IPR equation for gas wells and its application［J］.Well Testing，1998，7（4）：22－26.

［10］陈元千，闫为格.两种IPR方程在渤海油区的应用与评价［J］.油气井测试，2004，13（4）：13－19.

Chen Yuanqian，Yan Weige.The application and evaluation of two IPR equations on Bohai oil area［J］.Well Testing，2004，13（4）：13－19.

［11］TAREK A.Reservoir engineering handbook［M］.Houston，Texas：Gulf Publishing Company，2000：515－532.

Establishment and comparison of the IPR equations for horizontal wells

Chen Yuanqian Zhou Cui
（PetroChina Research Institute of Petroleum Exploration ＆Development，Beijing100083，China）

Based on the concept of equivalent drainage radius for vertical wells，the production equation of horizontal wells is transformed to that of vertical wells which has the equivalent production rate.Also，the binomial formula is established to predict the absolute open flow rate and inflow performance relationship curve for horizontal oil wells through single point drawdown test.So far，there are merely two IPR equations for horizontal oil wells abroad，namely，the Bendakhlia and Azis’s equation and Cheng’s revised formula.These two IPR equations were built from reservoir numerical simulation under solution gas drive condition.Compared to the equations abroad，the equation founded in this paper has the same form but opposite functional relationship and also has stronger theoretical basis.

oil reservoir；horizontal oil well；dimensionless IPR equation；productivity prediction

TE355.6

A

2014－10－11

（编辑：崔护社 杨 滨）

陈元千，周翠.水平油井IPR方程的建立与对比［J］.中国海上油气，2015，27（2）：44－47.

Chen Yuanqian，Zhou Cui.Establishment and comparison of the IPR equations for horizontal wells［J］.China Offshore Oil and Gas，2015，27（2）：44－47.

1673－1506（2015）02－0044－04

10.11935/j.issn.1673－1506.2015.02.007

陈元千，男，教授级高级工程师，长期从事油气藏工程和储量评价方面的研究。地址：北京市海淀区学院路20号中国石油勘探开发研究院（邮编：100083）。

等效驱动半径的概念和方法，将水平油井转成产量相同、形式相同的垂直油井，进而利用垂直油井的研究方法得到了水平油井的二项式方程，建立了利用单点测试资料预测水平油井绝对无阻流量和流入动态曲线的IPR方程。目前国外仅有针对溶解气驱条件，利用油藏数值模拟所得数据，由统计研究建立的Bendakhlia ＆Azis和Cheng 2个IPR经验方程。对比表明，本文提出的IPR方程与国外的2个IPR方程形式相同，函数关系相反，更具理论基础。