无穷积分的几个定理
蔡 瑾
(苏州健雄职业技术学院 软件与服务外包学院,江苏 太仓 215411)
无穷积分的几个定理
蔡 瑾
(苏州健雄职业技术学院 软件与服务外包学院,江苏 太仓 215411)
文章给出了关于无穷积分的三个定理及其证明,证明了收敛(或发散)的正值函数的无穷积分没有一个收敛(或发散)最慢的,且给出了构造收敛或发散更慢的无穷积分的一种方法.
无穷积分;收敛;发散
1 问题的提出
根据判别无穷积分的几种方法[1]188-204,本文讨论了关于正值函数f(x)使之无穷积分收敛与发散更慢的方法.


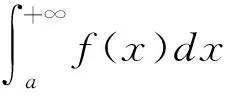





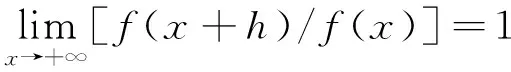

2 定理及证明





p>1时,x充分大时,f(x)≥1,所以fp(x)≥f(x)

0 又因∀ p<0,x充分大时,有f(x)≥1,fp(x)≤1, 经验定性法是根据区域的地貌特征、气候差异特点、水资源分布状况等客观存在的区域表现,主要考虑的是自然因素,常用来进行高级分区。本研究在用该方法时,主要考虑上述干旱分区指标体系中的地貌、降雨量和受灾率等3个自然因素,同时兼顾流域内干旱指数的因素,由于海拔较高的山区和丘陵区蓄水能力较弱,降雨量可能不能准确地反映当地的干旱程度,因此在这些地区以受灾率指标为主,降雨量指标为辅,而在海拔较低的丘陵和平原地区则以降雨量因素为主,受灾率指标为辅助指标,最后完成区域的一级干旱分区。 从而x充分大时,有 证明 令 (x)→C.(x→+∞) 令 由引理3知: 2)如果f(x)是单调递减趋于0,令F(x) 由引理3知: 通过本文的论证,能够得出一个很好事实,收敛的正值函数的无穷积分没有一个收敛得最慢的,在发散的正值函数的无穷积分中没有一个发散得最慢,并且给出了构造的方法.进一步证明了在比较法中,不存在普遍适用的函数. [1] 刘玉链,傅沛仁. 数学分析讲义[M].北京:高等教育出版社,1992. [2] 邹承祖. 数学分析习题课讲义[M].长春:吉林大学出版社,1986. [责任编辑 迎客松] 2015-07-12 江苏省现代教育技术研究2013 年度重点课题(项目编号:2013-R-25012) 蔡 瑾(1967- ) ,女,江苏太仓人,苏州健雄职业技术学院讲师,主要从事高等数学教学与研究工作。 1671-8127(2015)05-0001-03 O172.2 A









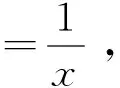
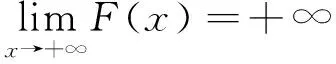

3 结语

