负顾客到达的Geo/G/1重试排队系统及在通信网中的应用

彭 赘

（长沙师范学院初等教育系，中国长沙 410100）

负顾客到达的Geo/G/1重试排队系统及在通信网中的应用

彭 赘*

（长沙师范学院初等教育系，中国长沙 410100）

研究了具有负顾客到达和一般重试时间的离散时间Geo/G/1重试排队系统.分析了其嵌入马氏链，得到了系统稳态存在的充要条件，利用补充变量法得到了系统演化的平衡方程组.通过求解这些平衡方程得到了嵌入马氏链的平稳分布.进而得到了一系列重要的排队性能指标.最后将此排队系统应用到蜂窝移动通信通信网中.数值实例说明系统各参数对排队性能指标的影响程度.

离散时间排队系统；重试；负顾客；马尔可夫链；蜂窝移动通信网络

近年来，越来越多的排队论学者感兴趣带负顾客的排队系统，这是因为带负顾客的排队系统在计算机通信网络和制造系统中有广泛应用.负顾客排队系统由Gelenbe［1］于1989年最先引入，目的是用来模拟神经网络.正顾客为通常意义上的顾客，即到达系统接受服务后离开系统.相对于正顾客而言，负顾客通常不接受服务，而对系统起破坏作用.负顾客到达系统时若系统中无正顾客，则离开系统而对系统无任何影响；若有正顾客，则按某种指定的移除法从系统中带走一个或多个正顾客，同时其自身也离开系统.“负顾客”概念的引入带来各种各样的应用.带负顾客的排队系统在计算机通信网络、生产制造系统、图像识别与处理和生物脑神经网络的模拟中有着非常重要的应用.尤其在随机神经网络领域里，“负顾客”的概念起着非常关键的作用.关于“负顾客”的理论和应用探讨的文献也随之越来越多［2-4］.上世纪有关带负顾客排队系统的主要研究方法及成果可参见Gelenbe［5］和Artalejo［6］.研究带负顾客的排队系统可以对生产制造系统，信号机操作系统，生物脑神经系统，计算机病毒对计算机数据的影响，通信网络中信元的转移与丢失，电话网络中呼叫的转移与丢失等提供一定的优化依据.关于带负顾客的离散时间排队系统的文献不多.Atencia［7］和Moreno［8］研究了带负顾客的离散时间Geo/Geo/1排队系统.Wang和Zhang［9］分析了带负顾客的离散时间Geo/Geo/1重试排队系统.Wu等人［10］考虑了一个顾客具有优先权和不耐烦性质的离散时间Geo/G/1重试排队系统.本文将负顾客引入到重试时间为一般分布的离散时间Geo/G/1重试排队系统中，得到了一系列重要的排队性能指标，同时说明了该排队系统在蜂窝移动通信网络中的应用.

1 模型描述

考虑一个单服务台的离散时间重试排队系统.在离散时间排队系统中，时间轴被分割成等长的时隙.在考虑的离散时间重试排队系统中的所有事件（例如顾客的到达和离去以及重试组中的顾客重试等）都只能发生在时隙的分点处.因此，所有事件可能在同一时刻发生.这样就必须规定这些事件发生的先后顺序.这里考虑早到系统（EAS）.假设时间轴被标记为0，1，…，m，….则正顾客和负顾客的到达、重试依次只能发生在时隙首端（m，m+）处，而服务完成只能发生于时隙（m-，m）处.这里m-表示时刻m前一瞬间，m+表示时刻m后一瞬间.关于早到系统及相关概念可参见Hunter［11］报道.

假设到达过程、服务过程和重试过程都是相互独立的.

2 模型分析及排队性能指标

在时刻m+，系统的演化行为可由马尔可夫过程｛Ym；m≥1｝来刻画，其中Ym=（Cm，ξ0，m，ξ1，m，Nm），Cm根据服务台空闲或忙而取值0或1，Nm表示重数组中的顾客数.若Cm=0且Nm＞0，则ξ0，m表示剩余重试时间.若Cm=1，则ξ1，m表示正在接受服务的顾客的剩余服务时间.

易知，过程｛Ym，m≥1｝是此排队系统的嵌入马氏链，其状态空间为｛（0，0）；（0，i，k）：i≥1，k≥1；（1，i，k）：i≥1，k≥0｝.本文的主要工作是求马尔可夫链｛Ym，m≥1｝的平稳分布：

令pyy′=P｛Ym+1=y′|Ym=y｝表示该链的一步转移概率，则根据系统的运行规律有：

若i≥1，k≥1，

若i≥1，k≥0，

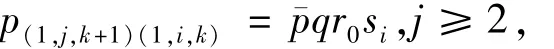
描述系统平稳分布的Kolmogorov方程为

其中δi，j是Kronecker记号.归一化条件为

为求解方程（1）～（3），引入如下母函数：

将方程（5）和（6）两边同乘以xi，然后对i求和，有

在方程（7）和（8）中令x=1，得到

将方程（9）代入（10）并解出φ1（1，z），得到

将式（11）代入式（9）并解出φ0（1，z），得到

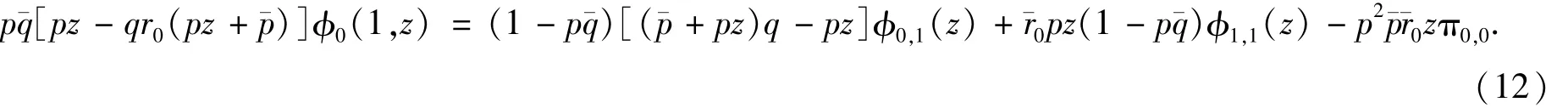
在式（7）中令x=1-p¯q，在式（8）中令x=（pz+¯p）¯q得

将式（11）和式（12）分别代入式（13）和式（14），得到

其中

由式（15）和式（16）得

最后，下述定理以母函数的形式给出了Kolmogorov方程组的解.通过这些母函数，可求得此嵌入马氏链的平稳分布及其性质.

定理1此嵌入马氏链平稳分布的概率母函数为

其中

证 证明上述定理只需将式（11），（12），（17）和（18）代入式（7）和式（8），即可推导出母函数φ0（x，z）和φ1（x，z）.最后再利用归一化条件可确定常数π0，0.

注1 注意到系统稳态存在的条件是π0，0＞0，即

3 数值实例及在蜂窝移动通信网络中的应用

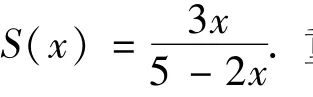
图1描绘了系统空的概率π0，0关于参数q的变化趋势.π0，0是关于负顾客到达率q的递增函数.负顾客到达率q对服务台忙的概率φ1（1，1）的影响效果由图2给出.π0，0是关于负顾客到达率q的递增函数.此外，观察到服务台忙的概率与重试间隔时间无关.这是因为几何分布具有无记忆性.

图3说明了重试组中的平均顾客数关于参数q的变化趋势.由图3可以看出，重试组中的平均顾客数随着负顾客到达率的增大而单调递减，这个结论也是显而易见的.必须说明的是当q趋近于1时，重试组平均队长L0几乎不受参数r0的影响.而且，随着q的减小，不同的r0值对L0的影响效果变得较发散.

图1 π0，0关于q的变化趋势Fig.1 π0，0versus q for different r0

图2 φ1（1，1）关于q的变化趋势Fig.2 φ1（1，1）versus q for different r0

图4给出了负顾客到达率对顾客平均逗留时间的影响效果.由图4可知，顾客的平均逗留时间随着负顾客到达率的增大而减少.这是由于负顾客的移除作用而引起的.

图3 L0关于q的变化趋势Fig.3 L0versus q for different r0

图4 平均逗留时间关于q的变化趋势Fig.4 W versus q for different r0

［1］ GELENBE E.Random neural networkswith negative and positive signals and product form solution［J］.Neural Comput，1989，25（1）：502-510.

［2］ GELENBE E.Product-form queueing networks with negative and positive customers［J］.JAppl Probab，1991，28（2）：656-663.

［3］ GELENBE E.G-networkswith triggered customermovement［J］.JAppl Probab，1993，30（2）：742-748.

［4］ GELENBE E.G-networks：a unifyingmodel for neural and queueing networks［J］.Ann Oper Res，1994，48（1）：433-461.

［5］ GELENBE E.The first decade of G-networks［J］.Eur JOper Res，2000，126（1）：231-232.

［6］ ARTALEJO JR.G-networks：A versatile approach forwork removal in queueing networks［J］.Eur JOper Res，2000，126（1）：233-249.

［7］ ATENCIA I，MORENO P.A single-server G-queue in discrete-time with geometrical arrival and service process［J］.Perform Eval，2005，59（1）：85-97.

［8］ ATENCIA I，MORENO P.The discrete-time Geo/Geo/1 queue with negative customers and disasters［J］.Comput Oper Res，2004，31（6）：1537-1548.

［9］ WANG J，ZHANG P.A discrete-time retrial queuewith negative customers and unreliable server［J］.Comput Ind Eng，2009，56（4）：1216-1222.

［10］ WU J，WANG J，LIU Z.A discrete-time Geo/G/1 retrial queuewith preferred and impatient customers［J］.ApplMath Model，2013，37（8）：2552-2561.

［11］ HUNTER JJ.Mathematical techniques ofapplied probability，vol.2，discrete-timemodels：techniques and applications［M］.New York：Academic Press，1983.

［12］ ATENCIA I，MORENO P.A discrete-time Geo/G/1 retrial queue with general retrial times［J］.Queueing Syst，2004，48（1）：5-21.

（编辑 陈笑梅）

A Geo/G/1 Retrial Queueing System w ith Negative Customers and Its Application in Communication Networks

PENG Yi*
（Junior Education Department，Changsha Normal University，Changsha 410100，China）

A discrete-time Geo/G/1 retrial queueing system with negative customers and general retrial times was studied.The Markov chain embedded to the considered queueing system was analyzed.The system state distribution aswell as the orbit size and the system size distributionswere obtained in terms of their generating functions，which yield exact expressions for different performancemeasures.Besides，the stability condition of the system was derived.Finally，an application to the cellularmobile communication network is provided and some numerical examples are provided to illustrate the impact of several parameters on some crucial performance characteristics of the system.

discrete-time queueing system；retrial；negative customer；Markov chain；cellularmobile communication network

O122

A

1000-2537（2015）04-0068-06

10.7612/j.issn.1000-2537.2015.04.012*

2015-02-27

国家自然科学基金资助项目（11201489）

*通讯作者，E-mail：pengyiqueue@163.com