弹弓效应原理简析

李品钧

（岭南师范学院基础教育学院，广东 湛江 524037）

张三慧教授编著的教材《大学物理学》[1：104-106]（以下简称《教材》）以例题的形式介绍了“弹弓效应”这一物理学的应用问题，文献[2]对其进行了更为深入细致的讨论.以探测器因掠过土星而在日心系内被加速的问题为例，在以上文献中，均隐含了如下的两个近似：（1）由于土星的质量远大于探测器的质量且两者“碰撞”时间相对比较短，故在整个“弹弓效应”过程（视为无接触“碰撞”）中，土星的运动状态（速度）不变.（2）若以土星中心作为参考系（土心系），则探测器机械能守恒，于是探测器的入射速率和出射速率相等.由此看来，这应是一个质量悬殊的两体问题，这类问题较为准确的近似处理在文献[3]中有详细的讨论.然而若基于以上两条近似，完全可以利用探测器速度在土心系和日心系之间的变换来简洁直观地说明“弹弓效应”的加速原理.这样做，有利于突出物理问题的过程，相反，若用两体问题中的典型分析方法——动量守恒加机械能守恒来处理，则弱化了整个加速过程由因到果的物理情景.另外，关于探测器的偏转角与瞄准距离之间的关系，也可以通过对照同为两体问题的散射理论而得出.

1 “弹弓效应”的加速原因

如图1（a）所示，一探测器掠过土星，可视为与土星发生了无接触的“碰撞”，《教材》正是用两体碰撞理论对这一过程进行分析，设置了一个特殊的过程，解得在日心系内探测器在“碰撞”之后的速率比“碰撞”之前要大，即“碰撞”使探测器获得了加速，是为“弹弓效应”，也称“引力推进”.下面用速度变换理论来解释该效应.

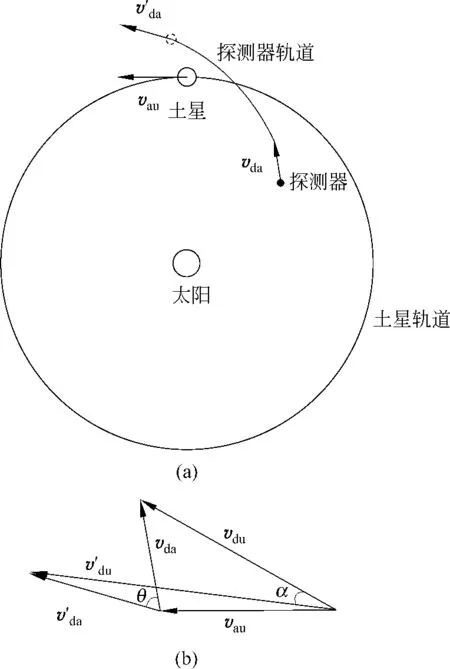
图1 弹弓效应原理

在土心系中探测器以vda的速度入射并掠过土星，然后以速度v′da出射，因机械能守恒，入射速率与出射速率应该相等.即

设土星在日心系中的速度为vau，则探测器在日心系中的入射速度

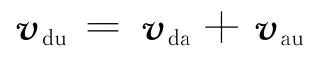
同样，在日心系中的出射速度

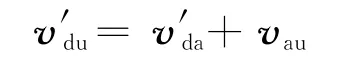
将上述两个矢量关系式绘成矢量图（见图1（b）），显然有

即在日心系中看来，探测器的出射速率比入射速率大.

由此可见，从速度在不同参考系内的变换这一角度来看，“弹弓效应”的实质无非是通过行星对探测器的引力改变了探测器在该行星参考系中的运动方向，使得相对速度vda与牵连速度vau的方向在出射后比入射前更接近，从而增大探测器在日心系中的速率vdu.当探测器的出射方向与土星运动方向相同时，探测器将获得最大的出射速率

《教材》的原例中选择日心系作为参考系，如图2（a）所示，土星的速率vau＝9.6km／s，探测器以速率vdu＝10.4km／s逆向土星飞行，绕过土星后沿与原来相反的方向飞离.求此飞离速率.

将参考系变换到土心系，则太阳的速度vua＝-vau，探测器速度

由图2（b），可得探测器的速率vda＝vdu＋vua＝（10.4＋9.6）m／s＝20.0m／s.

根据前文提到的“近似”，在土心系内探测器将以同样的速率出射且土星的速度不变.

2 弹弓效应的加速条件

探测器与土星“相撞”之后方向发生了偏转，出射速度与入射速度之间的夹角为偏转角.图1（b）中的θ即为探测器在土心系中的偏转角，而α为其在日心系中的偏转角.如前所述，探测器的出射方向与行星运动方向越接近，出射速度越大.当出射方向与行星运动方向完全相同时，出射速度最大（见图3（a））.设此时两参考系中的偏转角分别为θ0和α0，则探测器实现加速的偏转角在两个参考系中的范围分别是：0＜θ＜2θ0和0＜α＜2α0.超过这一范围，则起到减速（引力制动）的作用，如图3（b）所示，很明显＜vdu.由此可见，多数的偏转角是小于90°的，且出射方向常与行星轨迹平行（由此获得最大的出射速度）.卡西尼-惠更斯号探测器的飞行轨迹可以印证这一结论，见图4（图片来源于互联网[4]）.

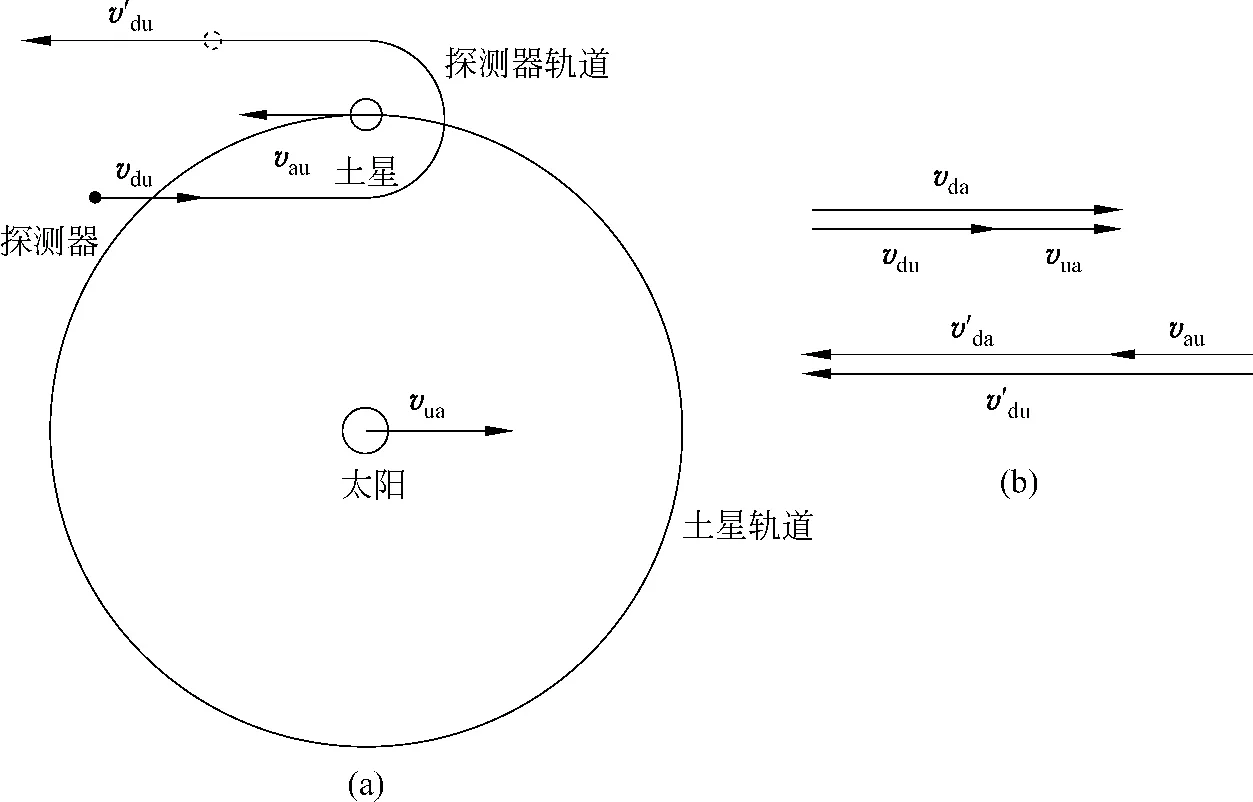
图2 《教材》原例示意图

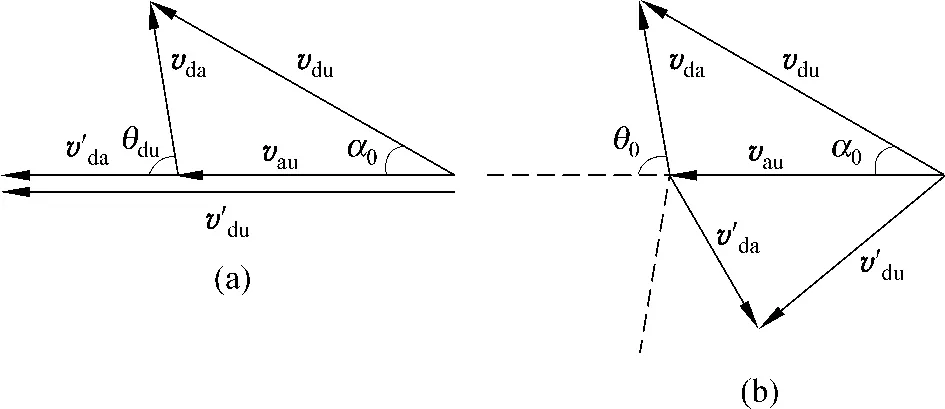
图3 出射速度与偏转角的关系

图4 卡西尼-惠更斯号探测器飞行轨迹

3 弹弓效应与α粒子散射中的偏转角对照分析

α粒子的散射角问题在很多普通物理类教材中都有涉及，在理论力学尤其原子物理学教材中更是一个必谈内容.巧合的是，在张三慧的这本《教材》中就将其作为例题，讨论了瞄准距离与散射角之间的关系[5：73-74].其实，弹弓效应又何尝不是一种散射？只不过与α粒子的散射相比较而言，前者为引力散射，后者为斥力散射，前者为汇聚散射，后者为发散散射（如图5所示）.

α粒子散射中入射粒子与靶粒子之间的斥力为

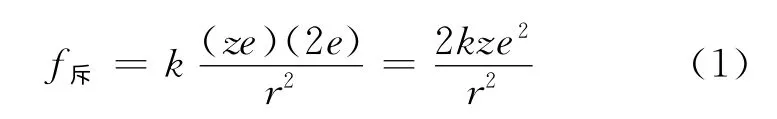
《教材》中推导出的散射角公式为

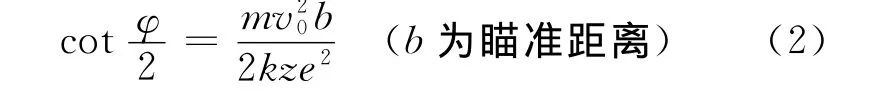
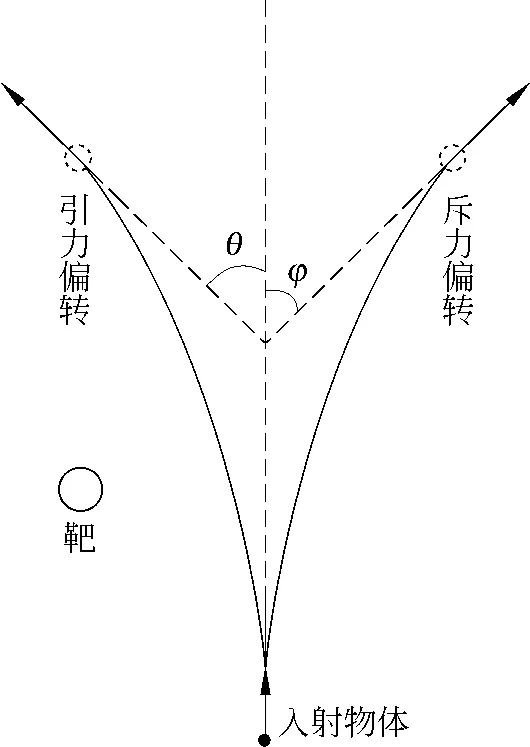
图5 引力偏转与斥力偏转

弹弓效应中探测器与行星之间的引力为

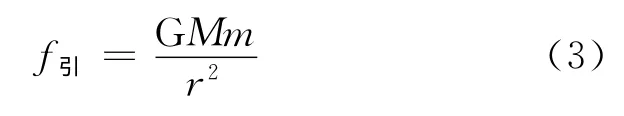
在这两类“散射”问题中，引力或斥力具备相同的形式（距离平方反比率），“散射角”（偏转角）的计算方式完全相同.注意到，式（2）中的分母即为式（1）中的分子，现只需将其用式（3）中的分子替换，即得弹弓效应中的偏转角所满足的等式

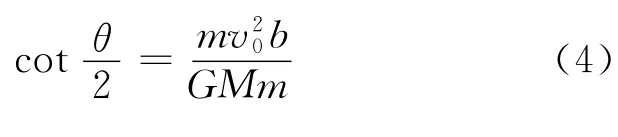
即

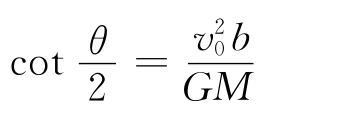
若将式（4）中的探测器质量考虑为折合质量，即

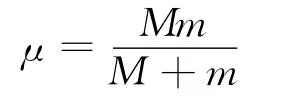
则可得到更为准确的散射角公式与文献[2]的结论相同.

4 普通尺度下的“弹弓效应”

通过两个质量差距较大的物体之间的碰撞，实现小质量物体在实验室参考系中得到加速的实例，在普通尺度上就有.如文献[5]提到的一个有趣的课堂演示实验：将一个小皮球（也可以用乒乓球——笔者注）放在一个大皮球的上面，使之自由落下.当它们落到地面上反弹时小球跳得比原来高许多倍（被加速弹出），往往会打到天花板上.这其实就是一个普通尺度上的弹弓效应，其加速原理在该文献上正是采用了速度变换的方式予以解释的.

以上用速度变换的方式简洁直观地解释了弹弓效应，将大尺度中的弹弓效应、小尺度中的粒子散射和一般尺度的两体问题联系起来，相互关照印证，有利于学生理解广泛的普通物理体系的两体问题，而非将其视作零散的知识点.

[1]张三慧.大学物理学：上册[M].3版.北京：清华大学出版社，2010：104-106.

[2]秦月婷.浅议弹弓效应[J].大学物理，2014（2）：26-27.

[3]胡明政，何荣良.质心系在近似问题中的特殊作用——质量悬殊的两体问题的近似处理[J].物理与工程，2007（3）：24-26.

[4]Nicholas M.Short，Sr.The Cassini-Huygens Mission[DB／OL].http：／／www.fas.org／irp／imint／docs／rst／Sect19／Sect19＿19.html.

[5]赵凯华，罗蔚茵.新概念物理教程：力学[M].北京：高等教育出版社，1995：145-146.