六圆弧蛋形断面正常水深直接计算方法
张志昌,贾 斌,李若冰
(西安理工大学 水利水电学院,陕西 西安710048)
六圆弧蛋形断面正常水深直接计算方法
张志昌,贾 斌,李若冰
(西安理工大学 水利水电学院,陕西 西安710048)
【目的】 研究六圆弧蛋形断面正常水深的简单计算方法,为该断面的工程设计提供技术支持。【方法】 根据面积分割法计算六圆弧蛋形断面的面积、湿周和水力半径,根据明渠均匀流理论计算不同流量时渠道的正常水深,通过优化拟合研究蛋形断面正常水深的简单计算方法。【结果】 优化拟合得到了蛋形断面水深处于不同位置时相对断面面积、相对湿周、相对水力半径的计算公式,确定了正常水深与流量的关系及水深的迭代计算公式,通过优化拟合研究,最后给出了正常水深的简化计算公式。【结论】 所建立的六圆弧蛋形断面正常水深的理论计算公式和近似计算公式计算过程简单、精度高,平均误差为0.204%,最大误差为1.129%。
六圆弧蛋形断面;正常水深;计算方法;参数修改
正常水深的计算在明渠设计、运行、维护中具有重要作用。明渠断面有矩形、梯形、U形、马蹄型、蛋形等多种形式,对于矩形和梯形断面正常水深的研究已有很多成果[1-3],对于U形断面文献[4]给出了直接计算公式,马蹄型断面分为标准Ⅰ型和标准Ⅱ型,对标准Ⅰ型马蹄型断面文献[5]给出了正常水深的迭代公式,文献[6]给出了标准Ⅱ型马蹄型断面正常水深的直接计算公式。
蛋形断面由于受力条件好,水流条件优越,常用于城市的排水工程和水工建筑物的隧洞工程。例如美国曼哈顿的排水工程、印度卡纳塔克邦Varahi水电站的输水工程[7],以及我国湖南省临澧县青山水轮泵站灌区的冉铺湾隧洞[8]和衡东县白莲灌区武家坳隧洞[9]均采用蛋形断面。
蛋形断面形状比较复杂,形式多样。断面形式主要有下部为半圆形、上部为半椭圆形的蛋形断面[10];底部为半圆形、上部为抛物线形的蛋形断面[9]和四圆弧蛋形断面[11]及六圆弧蛋形断面[7-8]等。目前有关蛋形断面水力特性的研究主要集中在正常水深和临界水深方面。就正常水深而言,文献[10]研究了下部为半圆、上部为半椭圆的蛋形断面正常水深的近似计算方法;文献[12]运用CAD技术, 编制了倒立式四圆弧蛋形断面诺谟图;文献[13]也对倒立式四圆弧蛋形断面的水力要素进行了分析,给出了正常水深的计算方法;文献[14]将倒立式四圆弧蛋形断面分成3个区域,分别给出了正常水深的迭代公式,与理论公式相比该迭代公式的误差小于1%;文献[15]研究了四圆弧蛋形断面隧洞正常水深的简易算法,但从公式结构来看其计算过程比较复杂;文献[11]研究了四圆弧蛋形断面的正常水深,但在计算时需借助表格查算,计算过程比较麻烦;文献[16]依据优化拟合理论,给出了我国目前应用的六圆弧蛋形断面正常水深的简化计算方法,但在计算湿周时误将底部弓形断面的半角当作全角,公式存在着明显的错误;文献[7]研究了另一种形式的六圆弧蛋形断面正常水深和临界水深的计算方法,与我国目前应用的六圆弧蛋形断面相比,其圆弧的圆心位置不同。
综上可以看出,蛋形断面正常水深的计算主要是针对四圆弧蛋形断面或者圆弧和椭圆组合形式。六圆弧蛋形断面由6个圆心和3个不同半径的圆弧组成,几何形状复杂,计算过程繁琐。因此,本研究在详细推导六圆弧蛋形断面正常水深计算公式的基础上,分析了蛋形断面相对面积、相对水力半径、相对湿周、相对流量与相对水深的关系,以期确定该断面正常水深的简化计算方法,从而为六圆弧蛋形断面的工程设计提供技术支撑。
1 蛋形断面的形状及参数
六圆弧蛋形断面是在文献[17]的基础上改进的。文献[17]在设计中取r1=280 cm,r2=120 cm,r3=85 cm,α1=25.375°(0.442 88 rad),α2=122.2°(2.132 79 rad),α3=27.066 7°(0.472 4 rad),α4没有给出角度,渠道最大宽度为r1,最宽处距渠底的距离为82 cm,但使用计算机绘图时发现,在每个圆弧与圆弧相切点都找不到切点。因此作者对原设计进行了修改,在修改中仍保持r1、r3、α1,由图1的几何关系计算得:hab=27.013 74 cm,h2=54.782 39 cm,h3=78.912 02 cm,r2=119.291 86 cm,α2=121.183 8°(2.115 06 rad),α3=29.408 1°(0.513 27 rad),α4=40.128 11°(0.700 37 rad)。为了使蛋形断面具有通用性,文献[18]将hab、h2、h3、r2、r3均换成r1的函数,得hab=0.096 478r1,h2=0.195 651 4r1,h3=0.281 829r1,r2=0.426 042r1,r3=(17/56)r1。
现以图1中ab、cd、ef作为分界线,对应水深分别为hab、hc d、hef,则可以将断面水深h分为4种情况,即h≤hab、hab≤h≤hc d、hc d≤h≤hef和h≥hef。
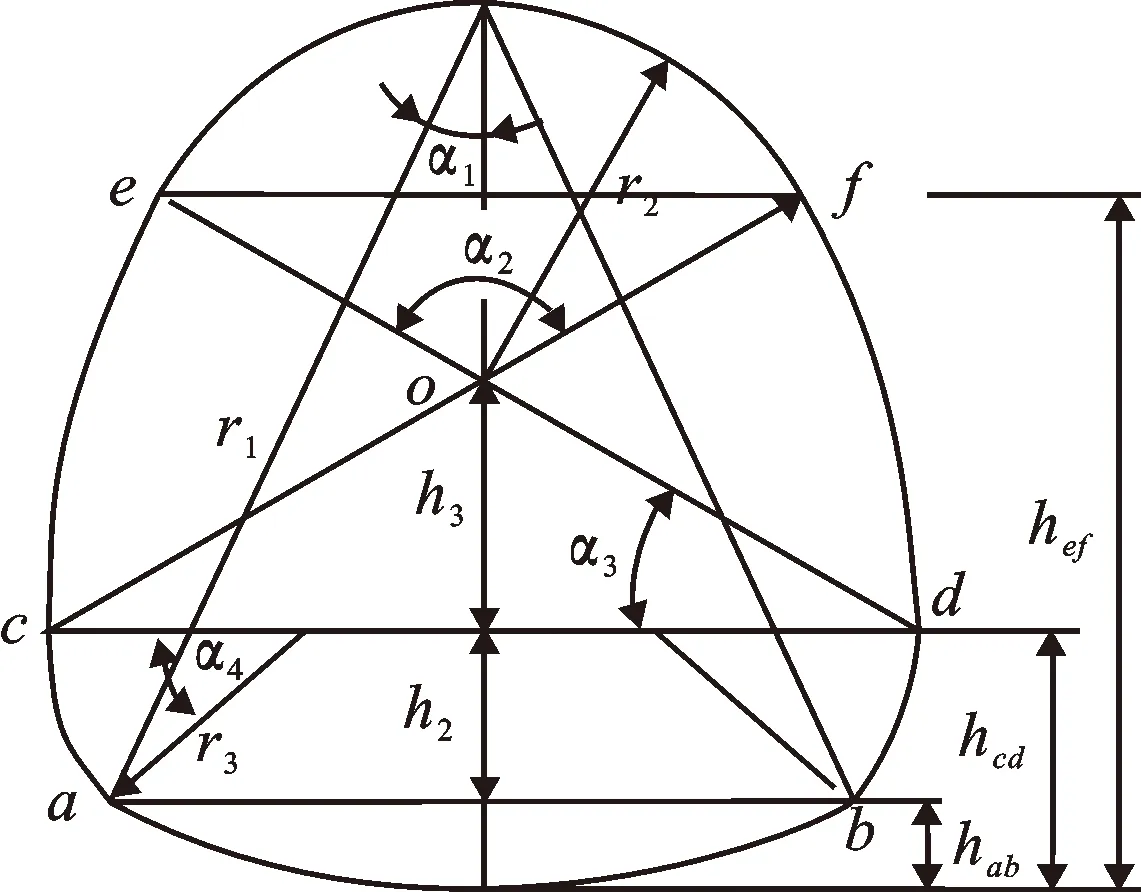
图1 蛋形断面设计示意图Fig.1 Diagrammatic design of egg-shaped cross section
2 不同水深时蛋形断面面积、湿周、水力半径和水深的计算
2.1 水深处于底部弓形断面(h≤hab)
如图2所示,当断面实际水深h处于底部弓形,即h≤hab时,断面相对面积、相对湿周、相对水力半径及相对水深按照下列公式计算。
断面相对面积为:
(1)
式中:A0为水深h对应的断面面积;φ为水深h处于底部弓形断面时对应的半角。
相对湿周为:
χ/r1=2φ。
(2)
式中:χ为湿周。
相对水力半径为:
R/r1=A0/(χr1)=(2φ-sin 2φ)/(4φ)。
(3)
式中:R为水力半径。
相对水深为:
h/r1=1-cosφ。
(4)
以上各式中,0<φ≤25.375°(0.442 88 rad)。
2.2 水深处于最大宽度以下(含最大宽度)断面(hab≤h≤hcd)
如图3所示,当断面实际水深h处于最大宽度以下时,可将计算区域分为底部、两侧弓形和中央梯形4个部分,其面积分别为A1、A2、A3、A4,文献[18]给出的相对断面面积计算公式为:
(5)
式中:α4=40.128 11°(0.700 37 rad),sin (α4-β)=sinα4cosβ-cosα4sinβ,代入公式(5)有:
(6)
同理,相对湿周、相对水力半径和相对水深的计算公式为:
χ/r1=2α1+(34/56)(α4-β)=1.310 978-(34/56)β,
(7)
R/r1=[0.242 5-(17/56)2(β+sinβcosβ)-0.119 26sinβ]/[1.310 978-(34/56)β],
(8)
h/r1=(hab+h2-r3sinβ)/r1=0.292 129-(17/56)sinβ。
(9)
式中:0≤β≤40.128 11°(0.700 37 rad)。
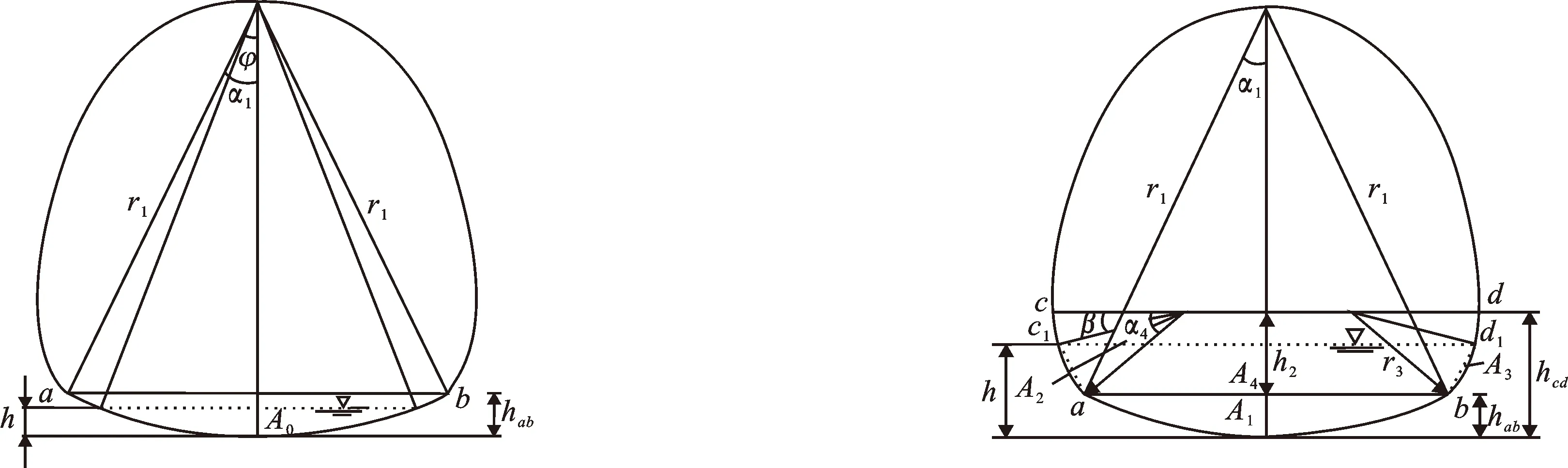
图2 水深处于底部弓形断面Fig.2 Water depth at the bottom bow of cross section
2.3 水深处于ef线(含ef线)以下断面(hcd≤h≤hef)
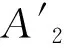
(10)
χ/r1=2α1+(34/56)α4+2β1=1.310 978+2β1,
(11)
R/r1=(0.242 5+β1-sinβ1+sinβ1cosβ1)/(1.310 978+2β1),
(12)
h/r1=0.292 129+sinβ1。
(13)
式中:0≤β1≤29.408 1°(0.513 27 rad)。
2.4 水深处于顶部弓形(ef线以上)断面(h≥hef)
当断面水深h处于图5的ef线以下时,在ef线以下(含ef线)的相对断面面积可以由公式(10)计算,此时的β1=α3=29.408 1°(0.513 27rad)。当断面水深h处于图5的ef线以上时,在ef线以上面积可以分为两侧弓形面积A8、A9及中间梯形面积A10。
相对断面面积、相对湿周、相对水力半径和相对水深的计算公式为:
(14)
χ/r1=2.337 514+0.852 084β2,
(15)
R/r1={0.614 854+0.181 512[β2+0.5sin (α-2β2)]}/(2.337 514+0.852 084β2),
(16)
h/r1=0.573 958+0.426 042cos (α2/2-β2)。
(17)
式中:0≤β2<α2/2=60.591 9°(1.057 53 rad)。
图4 水深处于ef线(含ef线)以下断面 Fig.4 Water depth under the ef line of cross section
3 蛋形断面正常水深的计算
3.1 不同断面水深条件下正常水深的理论计算
蛋形断面正常水深的计算公式为明渠均匀流公式[19],即:
(18)
式中:Q为流量,A为过水断面面积,C为谢才系数,R为水力半径,i为明渠的比降,n为糙率,χ为湿周。
由前面研究可以看出,六圆弧蛋形断面可以分为h≤hab、hab≤h≤hcd、hcd≤h≤hef和h≥hef4种断面水深条件,表1给出了4种水力条件下已知水深求流量和已知流量求水深的计算公式及迭代初值。
迭代公式经验算均收敛,由于证明过程较繁,此处从略。

表1 六圆弧蛋形断面正常水深的计算公式Table 1 Formula for normal water depth of Six arc egg-shaped section
3.2 蛋形断面正常水深的近似计算
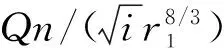
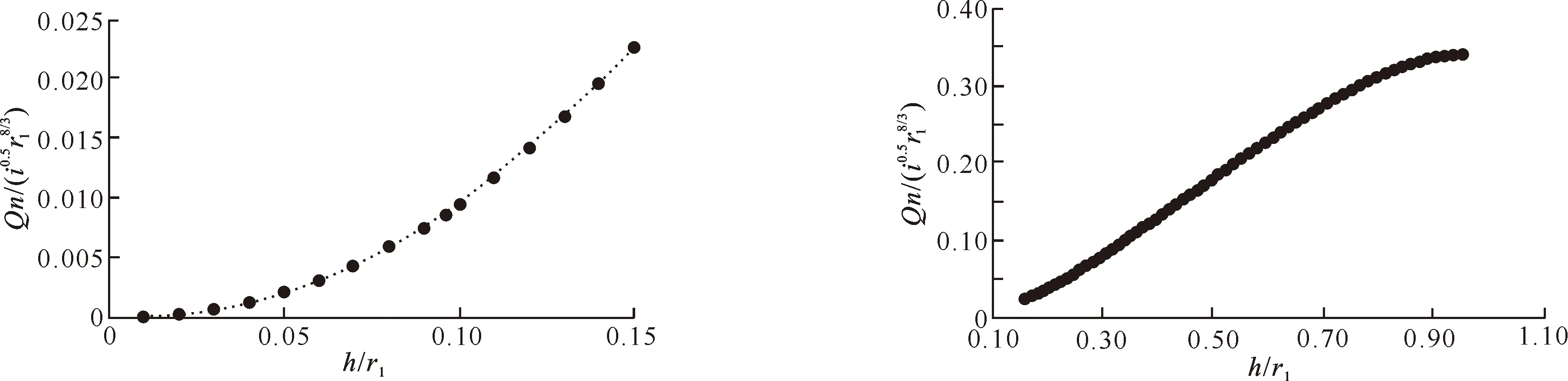
图6 当0 当0 (19) (19)式的平均误差为0.336%,最大误差为1.074%。 当0.15≤h/r1<0.90时,有: (20) (20)式的平均误差为0.204%,最大误差为1.129%。 (21) (22) 在迭代时,h/r1初值可取0.15~0.90。 公式(22)需要迭代求解,为了简化计算,给出的显函数关系式为: (23) 公式(23)的平均误差为0.229%,最大误差为1.057%。 已知某输水隧洞为六圆弧蛋形断面,最大半径r1=1.5 m,洞底设计坡降i=1/2 500,洞内壁糙率n=0.014,试求当设计流量Q=0.1~1.2 m3/s时隧洞内相应的正常水深h值。 根据设计流量及已知条件,由表1迭代法及公式(22)、(23)得到的正常水深h的计算结果及误差分析见表2。 表2 某六圆弧蛋形断面输水隧洞不同流量下正常水深的计算结果及误差分析Table 2 Calculation results and error analysis of normal water depth of egg-shaped cross section with six arcs in water-conveyance channel 由表2可以看出,h理论计算值与用简化公式计算的h值非常接近,最大误差为0.723%。而文献[16]由于湿周公式有误,在流量Q=0.1和1.2 m3/s时,计算得到的h=0.19和0.934 3 m,与h理论计算结果分别相差18.78%和13.77%。由此可见,水深越小,湿周对流量计算的影响越大。 本研究根据面积分割法和明渠均匀流理论,推导了六圆弧蛋形相对断面面积、相对湿周和相对水力半径的计算公式,给出了水深处于不同位置时正常水深与流量的关系,在此基础上,拟合了相对水深与相对流量的简单计算公式,经验证,该公式不仅计算方便而且精度较高,完全可以满足工程设计要求。 [1] 张志昌,肖宏武,毛兆民.明渠测流的理论和方法 [M].西安:陕西人民出版社,2004:292-293. Zhang Z C,Xiao H W,Mao Z M.The theory and method of the open channel flow [M].Xi’an:Shaanxi People’s Publishing House,2004:292-293.(in Chinese) [2] 赵延风,祝晗英,王正中,等.梯形明渠正常水深的直接计算方法 [J].西北农林科技大学学报:自然科学版,2009,37(4):220-223. Zhao Y F,Zhu H Y,Wang Z Z,et al.A direct formula for normal depth in trapezoidal open channel [J].Journal of Northwest A&F University:Natural Science Edition,2009,37(4):220-223.(in Chinese) [3] 王正中,席跟战,宋松柏,等.梯形明渠正常水深直接计算公式 [J].长江科学院院报,1998,15(6):1-3. Wang Z Z,Xi G Z,Song S B,et al.A direct calculation formula for normal depth in open trapezoidal channel [J].Journal of Yangtze River Scientific Research Institute,1998,15(6):1-3.(in Chinese) [4] 张新燕,吕宏兴,朱德兰.U形渠道正常水深的直接水力计算公式 [J].农业工程学报,2013,29(14):115-119. Zhang X Y,Lü H X,Zhu D L.Direct calculation formula for normal depth of U-shaped channel [J].Transactions of the CSAE,2013,29(14):115-119.(in Chinese) [5] 张志昌,李若冰.标准Ⅰ型马蹄形断面水力特性的研究 [J].长江科学院院报,2013,30(5):55-59. Zhang Z C,Li R B.Hydraulic characteristics of standard Ⅰ-type horseshoe cross section [J].Journal of Yangtze River Scientific Research Institute,2013,30(5):55-59.(in Chinese) [6] 赵延风,王正中,芦 琴.马蹄形断面正常水深的直接计算公式 [J].水力发电学报,2012,31(1):173-177. Zhao Y F,Wang Z Z,Lu Q.Direct calculation formulas for normal depth of horseshoe section [J].Journal of Hydroelectric Engineering,2012,31(1):173-177.(in Chinese) [7] Raikar R V,Shiva Reddy M S,Vishwanadh G K.Normal and critical depth computations for egg-shaped conduit sections [J].Flow Measurement and Instrumentation,2010,21(3):367-372. [8] 傅功年,唐耿红.冉铺湾隧洞衬砌断面型式选择 [J].人民长江,2002,33(5):14-16. Fu G N,Tang G H.Type selection of lined cross-section for Ranpuwan tunnel [J].Yangtze River,2002,33(5):14-16.(in Chinese) [9] 王子宜.蛋形衬砌在白莲灌区武家坳隧洞中的应用 [J].湖南水利水电,2006(6):70-71. Wang Z Y.Application of egg-shaped lining in Bailian irrigation area Wujiaao tunnel [J].Hunan Hydro & Power,2006(6):70-71.(in Chinese) [10] 李风玲,文 辉,涂宁宇.蛋形断面管道正常水深近似算法 [J].人民长江,2008,39(18):77-78. Li F L,Wen H,Tu N Y.Approximation algorithm of normal depth in egg-shaped cross section pipeline [J].Yangtze River,2008,39(18):77-78.(in Chinese) [11] Gill M A.Hydraulics of partially filled egg sewers [J].Journal of Environmental Engineering,1987,113(2):407-425. [12] 宁希南.蛋形断面管道简明水力计算及其诺谟图[J].林业建设,2007(5):22-25. Ning X N.Concise hydraulic calculation and nomogram of egg-shaped cross section pipeline [J].Forestry Construction,2007(5):22-25.(in Chinese) [13] 陶 冶,贾 悦.蛋形断面排水无压管道水力计算及其水力要素分析 [J].给水排水,2009,35(S1):428-430. Tao Y,Jia Y.Analysis of the hydraulic calculation and hydraulic elements of egg-shaped cross section in open channel [J].Water & Wastewater Engineering,2009,35(S1):428-430.(in Chinese) [14] Bijankhan M,Kouchakzadeh S.Egg-shaped cross section:Uniform flow direct solution and stability identification [J].Flow Measurement and Instrumentation,2011,22(6):511-516. [15] 滕 凯.蛋形断面隧洞正常水深的简易算法 [J].长江科学院院报,2013,30(12):39-42. Teng K.The simple algorithm of normal depth in egg-shaped cross section tunnel [J].Journal of Yangtze River Scitentific Research Institute,2013,30(12):39-42.(in Chinese) [16] 滕 凯,李新宇.六圆弧蛋形断面无压隧洞水面线解析计算模型 [J].水资源与水工程学报,2013,24(4):174-179. Teng K,Li X Y.Calculation model of water surface line analysis in tunnel of six circular egg-shaped section without pressure [J].Journal of Water Resources&Water Engineering,2013,24(4):174-179.(in Chinese) [17] 武汉水利电力学院.水工建筑物 [M].北京:水利出版社,1980:188-190. Wuhan Institute of Hydraulic and Electric Engineering.Hydraulic structure [M].Beijing:Water Conservancy Press,1980:188-190.(in Chinese) [18] 李若冰,张志昌.明渠六圆弧蛋形断面临界水深和收缩断面水深的计算 [J].武汉大学学报,2012,45(4):463-467. Li R B,Zhang Z C.Calculation of critical water depth and contraction section water depth in egg-shaped cross-section with six arcs of open channel [J].Engineering Journal of Wuhan University,2012,45(4):463-467.(in Chinese) [19] 张志昌.水力学 [M].北京:中国水利水电出版社,2011. Zhang Z C.Hydraulics [M].Beijing:China Water Power Press,2011.(in Chinese) Direction calculation of normal water depth of egg-shaped cross section with six arcs in open channel ZHANG Zhi-chang,JIA Bin,LI Ruo-bing (InstituteofWaterResourcesandHydro-electricEngineering,Xi’anUniversityofTechnology,Xi’an,Shaanxi710048,China) 【Objective】 This study proposed a simple method to calculate the normal water depth of egg-shaped cross section with six arcs to provide basis for engineering design of such section.【Method】 Based on area segmentation method,the area,wetted perimeter and hydraulic radius were computed.Using open channel uniform flow theory,the normal depths were studied under different flows and the approximate fitting was used to obtain simple calculation method of normal water depth.【Result】 Approximate fitting was used to obtain the simple calculation methods of section area, wetted perimeter and hydraulic radius at different positions.The relationship between normal depth and rate of flow,the iterative calculation formula of the water depth and the relationship between relative water depth and relative flow were also determined.At last,the simplified calculation method of normal water depth was proposed by optimizing fitting.【Conclusion】 The proposed theoretical calculation formula and approximate calculation formula of normal water depth of egg-shaped cross section were simple and precise with average error of 0.204% and maximum error of 1.129%. egg-shaped cross section with six arcs;normal depth;computing method;parametric modification 2014-01-20 张志昌(1954-),男,陕西西安人,教授级高级工程师,主要从事水工水力学研究。 E-mail:zhangzhichang1954@163.com 时间:2015-06-30 13:47 10.13207/j.cnki.jnwafu.2015.08.022 TV133 A 1671-9387(2015)08-0229-06 网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20150630.1347.022.html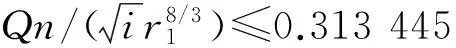
4 算 例
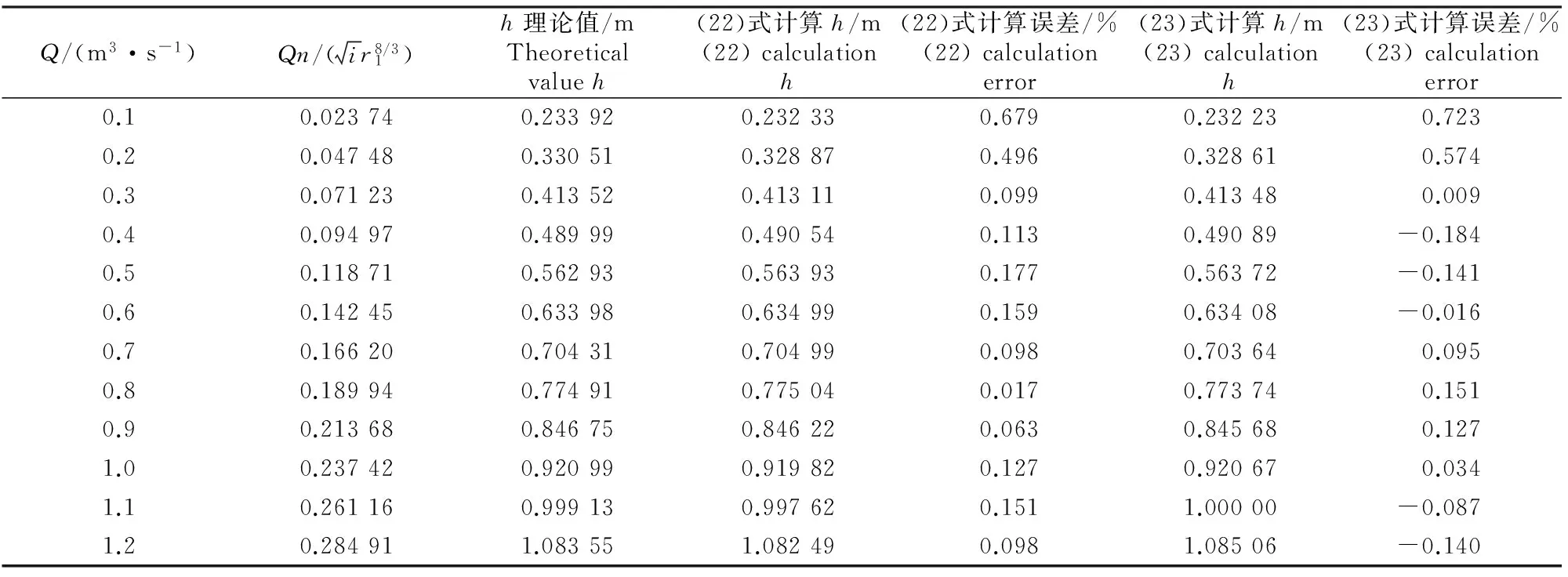
5 结 语

