基于流场的变截面动涡盘热应力变形分析

刘涛，王永威

(兰州理工大学 机电工程学院， 甘肃 兰州 730050)

基于流场的变截面动涡盘热应力变形分析

刘涛，王永威

(兰州理工大学 机电工程学院， 甘肃 兰州 730050)

建立了变截面动涡旋盘的三维几何模型。选择结构单元SOLID185，生成其有限元模型。对涡旋压缩机流场分析得到的模拟结果，进行插值拟合处理，得到了涡旋盘表面与压缩工质的对流换热系数及温度分布函数。由此对变截面动涡盘分别在线性温度场和基于流场分析的温度场进行热分析，得到了两种热边界载荷情况下涡旋盘的温度场分布，以及热变形和Mises应力结果。比较动涡盘的两种分析结果，说明涡盘热载荷的线性简化是合理的，基于流场的有限元分析更加符合涡旋压缩机的实际工况。

压缩机；涡旋盘；变截面； 流场； 热应力； 热变形

0 引言

涡旋压缩机以其体积小、结构简单、振动小和运转平稳等诸多优点受到了现代工业的广泛重视和应用。涡旋压缩机的工作是依靠动、静盘的啮合实现气体压缩的，动、静盘涡旋盘受力变形对涡旋压缩机的工作性能和可靠性会产生很大影响，因此有关涡旋压缩机工作过程中涡旋齿应力及变形一直是研究的热点。然而在涡旋压缩机运行过程中，动静涡旋盘相互啮合位置随着主轴转角的变化而变化，这就使涡旋盘的载荷分析变得非常复杂。

目前很多文献都对涡旋盘受气体压力载荷和热载荷进行了分析，并求得相应的应力和变形。文献[1-3]对气体压力和热载荷作用下的动涡旋盘的应力和变形进行了分析，找到了最大应力位置并分析两种载荷对啮合间隙的影响。但是该分析中对于热载荷处理过于简单，仅仅认为温度在整个涡旋盘的分布为线性分布；文献[4]采用实验的方法，在静涡旋盘安装温度传感器，测量出静涡旋盘在工作时测量点的温度值，然后利用有限元软件ABAQUS分析得到了涡旋盘的温度场，并分析了其热载荷下的应力和变形。文献[5]先对涡旋压缩机内部流场进行分析，得到压力场，温度场等压缩工质的状态，然后把流场分析的温度结果加载到涡旋盘，分析涡旋盘的温度场。文献[6]分析了涡旋盘在无温度场，40℃温度场和最高温度为85℃的线性温度分布的温度场3种情况与气体力耦合时的应力与变形。

首先对温度在变截面动涡旋盘为线性分布的情况进行了分析，得到了其温度场，热应力和热变形。然后，利用已有流场分析得到的压缩腔内的工质温度分布，经过处理后加载到动涡旋盘，分析得到涡旋盘的温度场，热应力和热变形，比较了两种温度场简化分析方法的优劣。

1 变截面涡旋盘的有限元模型

1.1 涡旋盘的几何模型

变截面涡旋盘基本几何参数：基圆半径2.6mm，涡旋型线终止展角4.5π，涡旋齿高度40mm，涡旋盘端板厚度10mm，端板直径110mm。涡旋型线包括圆渐开线和高次曲线，齿头部位采用PMP型线修正，非啮合部分为圆弧。在Pro/E中，依据涡旋型线的参数方程建立涡旋盘的三维模型。如图1所示。

图1 变截面动涡旋盘

1.2 涡旋盘的材料参数

变截面动涡旋盘材料选择铸铁(FC250),基本参数：弹性模量E=113GPa，泊松比μ=0.26，密度ρ=7150kg/m3,膨胀系数α=1.33×10-7/℃，导热系数λ=0.0526W/mm℃。

1.3 涡旋盘的约束条件

在涡旋压缩机实际工作中，动盘做公转平动，其约束为：1) 动涡盘与支架接触的部分，限制沿z轴方向的自由度；2) 与动盘相连接的十字滑环，限制沿z轴的自转；3) 动盘与曲柄稍接触的轴承座内，限制动盘沿x轴和y轴方向的自由度；4) 静盘静止，限制所有方向的自由度。

在利用ANSYS进行数值分析时，将以上实际约束简化为:1) 限制端板z轴方向的移动自由度；2) 轴承座内部环形面的移动和转动自由度完全限制。

1.4 涡旋盘的网格划分

变截面涡旋盘的几何形状比较复杂，为了保证网格划分的品质，以及分析结果的精度，现选择热分析单元Thermal Solid 87,10节点四面体单元划分网格。分析动盘温度场完成后，要转换有限元模型的单元类型为Structure Solid185，再进行热应力及热应变的分析。对动涡盘网格划分的结果为：单元为51866个，节点为82419个。具体网格划分结果，如图2。

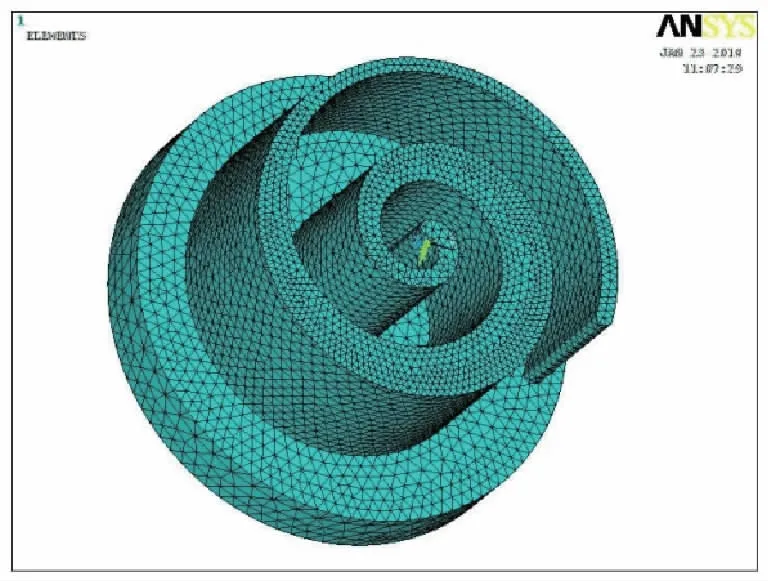
图2 动涡旋盘网格划分

2 涡旋盘的两种边界载荷

2.1 涡旋齿的热传递简化模型

在利用有限元方法分析涡旋盘的温度场时，需要首先分析涡旋齿两侧工作腔的热量传递过程。对应主轴每转一个角度，动涡旋盘对应的吸气腔，压缩腔和排气腔都发生了变化。为了更好的说明涡旋齿的热传递过程，把涡旋齿简化为一个二维的长条形状，如图3所示。在每一时刻涡旋齿内侧的压缩工质的温度始终要高于涡旋齿外壁。

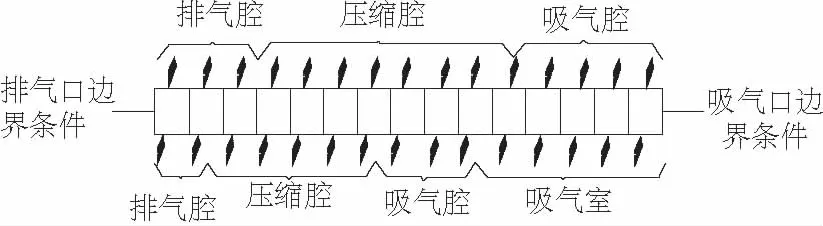
图3 动盘热量传递过程

2.2 温度线性变化的边界载荷

将涡旋盘的温度简化为沿涡盘端板半径方向呈线性递减变化，考虑到涡旋压缩机实际吸气、排气温度，线性变化的温度最高温度为100℃，最低温度为40℃。具体温度边界变化规律为：

T=40+60(1-x/0.055)。

式中：x(m)为柱坐标系下的涡旋盘端板半径；0.055(m)是涡旋盘端板的最大半径。

2.3 基于流场的热边界载荷

由变截面涡旋压缩机的流场数值模拟结果可以获得压缩腔内，动涡旋盘表面部分温度值以及对流换热系数。文中计算了这些位置在瞬态分析整个过程的平均值，具体如表1与表2所示。然后利用Matlab中插值拟合函数(regress)，获得了二维动涡旋盘的边界热载荷。由于涡旋盘沿齿高方向的参数变化很小，所以把二维热边界载荷作为三维变截面动涡旋盘的热载荷。

表1 涡盘边界对流换热系数值 W/m2·℃

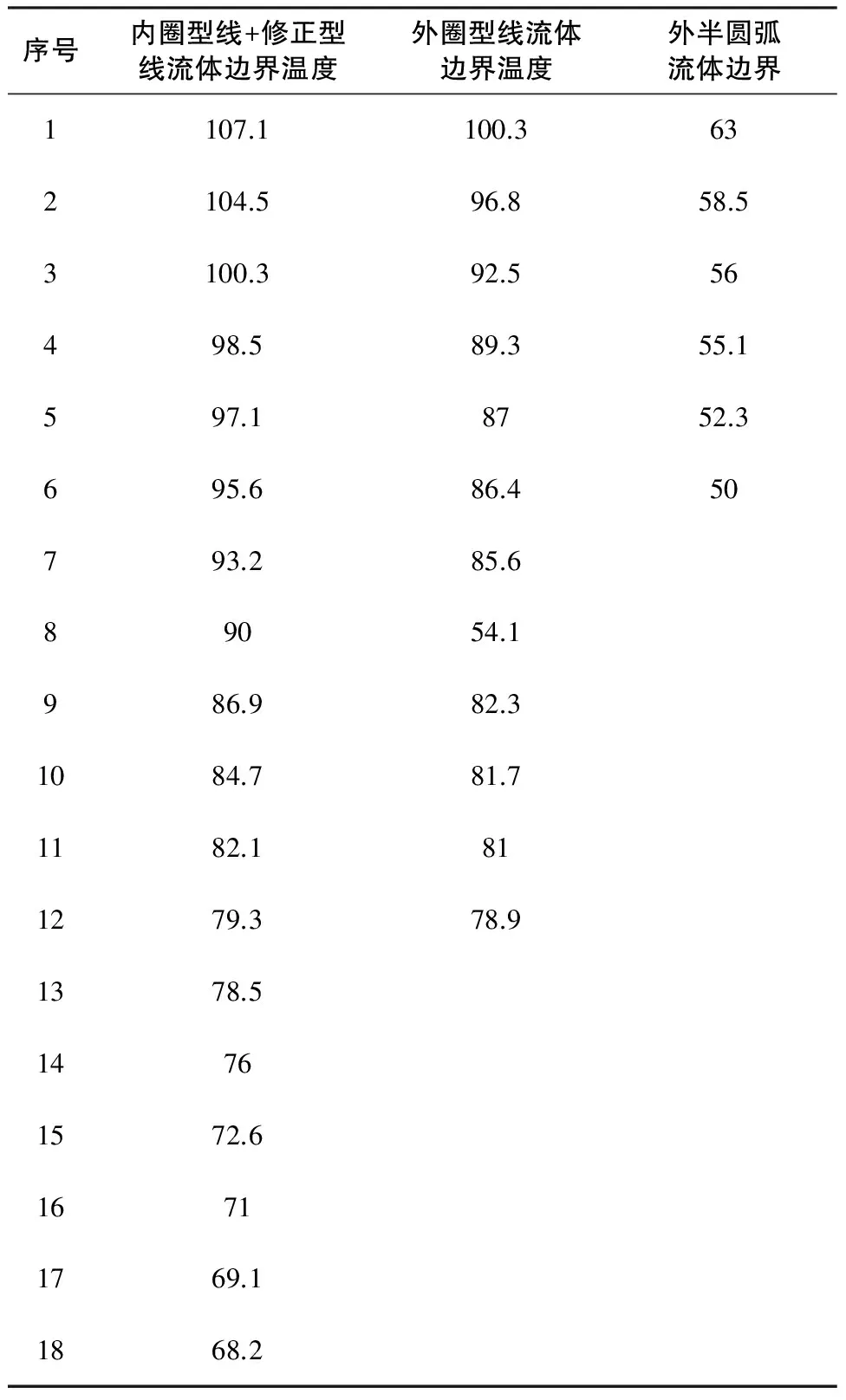
表2 涡盘边界温度值 ℃

1) 二维模型边界对流换热系数

由于非啮合圆弧部分一直处于吸气室，所以认为其对流换热系数为常数：820W/m2·℃。

涡旋盘外圈型线处的边界对流换热系数：

h=1859.2+40.7×R-89.3×φ-10.3×φ2

(1)

涡旋盘内圈型线和修正型线处的边界对流换热系数

h=1820.8-10.1×R-13.9×φ-1.8×φ2

(2)

2) 二维模型边界温度

非啮合圆弧部分的边界温度分布：

T=218.083 6+1.7036×R-22.6846×φ+0.464×φ2

(3)

涡旋盘外圈型线处的边界温度分布：

T=108.011+0.5495×R-4.789×φ+0.0661×φ2

(4)

涡旋盘内圈型线和修正型线处的边界温度分布

T=96.9372-0.3659×R-1.744×φ+0.0594×φ2

(5)

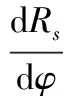
对于涡旋齿端面和涡旋盘端板其边界温度分布规律采用线性变化温度分布，即：T=40+60(1-x/0.055)。

文中所选的环境温度为30℃。将热边界载荷施加于涡旋盘实体的表面上，ANSYS程序自动将其转换到对应的节点上。

3 计算结果及分析

涡旋盘边界温度线性分布的分析结果如图4所示，温度由中心到外面逐渐降低，最高温度99.87℃出现在涡旋齿头部位。基于流场分析结果的涡旋盘温度场分析结果与前者最高温度99.93℃几乎相同，但涡旋齿部分的温度分布规律发生了变化，温度分布更符合实际情况，如图5所示。两种热边界载荷的热应力，总变形，Mises应力及涡旋盘z向变形结果见表1。两种热边界载荷分析的结果都表明，最大Mises应力位于东涡旋齿最内圈与静涡旋盘啮合的齿根处。由于分析求解时，对于涡旋盘端板底面施加了z方向的约束，所以最大变形位于涡旋齿头部位。总体来看，由于热涨冷缩，变截面涡旋盘整体呈现外凸的趋势，局部也存在内凹的现象。

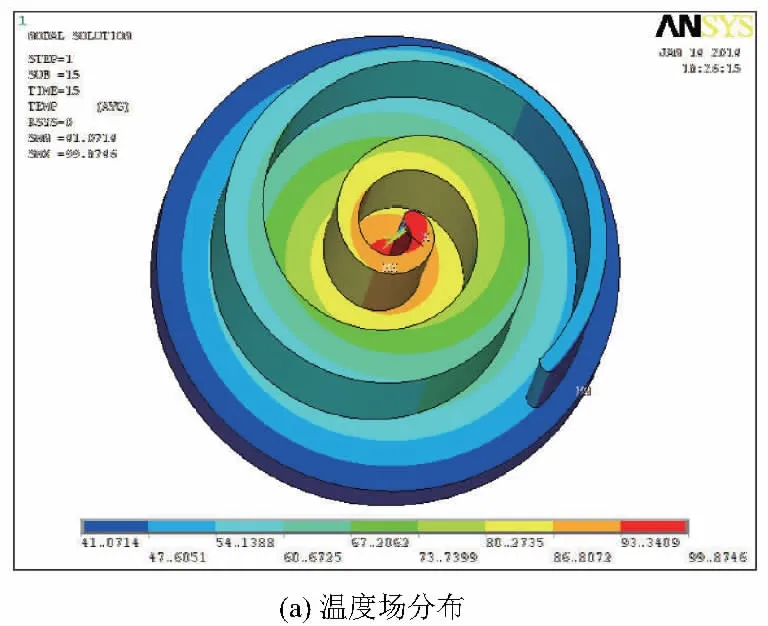
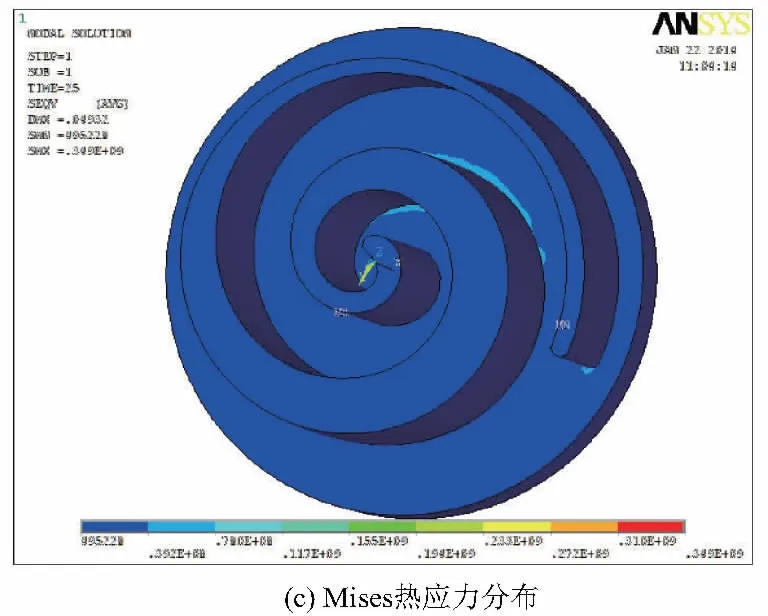
图4 边界载荷为线性温度的涡旋盘热分析

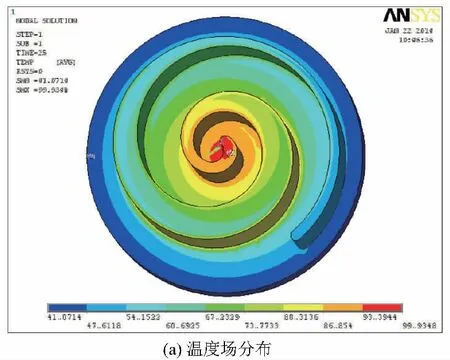
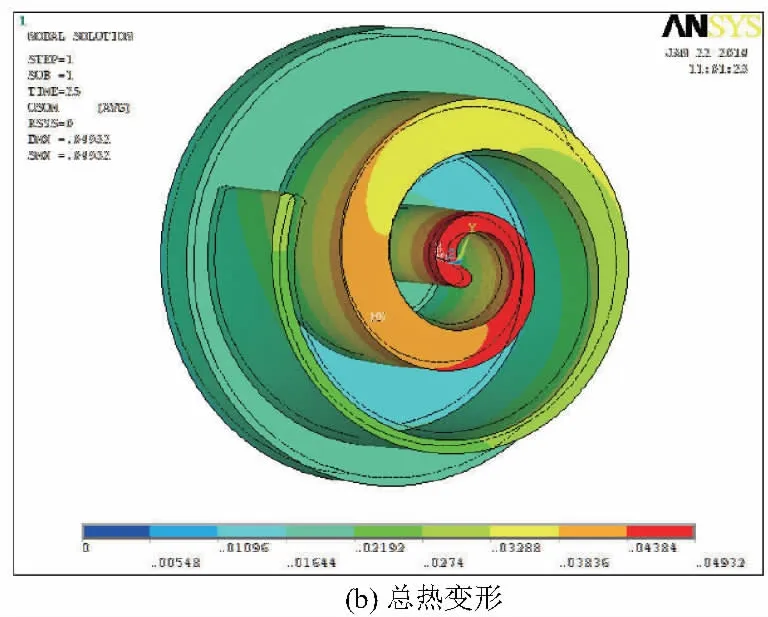
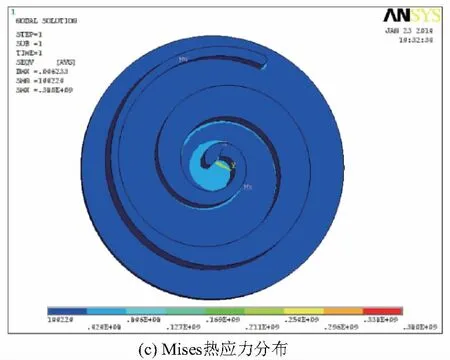
图5 基于流场分析结果的涡旋盘热载荷分析

由表3可以得到，变截面涡旋盘在两种热边界载荷条件下的变形与应力结果。对比分析可以知道，采用基于流场分析结果的热载荷时其变形要更大一些，然而其最大热应力比温度线性变化时的分析结果小。这是由于经流场分析得到的温度场更加符合涡旋压缩机实际工况，其涡旋盘的温度场分布更加合理。

4 结语

1) 由表3数据以及涡旋盘温度场的分布可以知道，两种热边界载荷应用于动涡旋盘的结构分析时，其热变形及Mise应力计算结果相差不大。但是基于涡旋压缩机内部流场流动得到的动涡盘温度场，其与采用线性温度简化的方法不同，特别是在涡旋齿壁处温度的分布。计算结果表明，两种方法都可以用于涡旋盘热应力与变形计算时的温度载荷。

表3 两种边界载荷的热分析结果

2) 在涡旋压缩机工作中，变截面动涡旋盘在压缩结束时刻的应力和变形最大，这是由于此时该处的温度最高。相比较之后，发现两种热边界载荷条件下，应力最大部位位于涡旋齿头部位的齿根处，变形最大出现在涡旋齿齿头的齿顶处。所以在压缩机工作过程中，动涡盘的齿头部位为最危险位置。

3) 综上所述，虽然两种温度场求解方法在涡盘结构分析中差别不大，但是应该尽量依据涡旋压缩机工作的实际工况简化模型，以及相关的载荷边界条件，才能得到符合实际、可靠的分析结果。

[1] 金丹, 陈旭, 田涛. 非均匀温度场下涡旋压缩机动涡盘的应力及变形分析[J]. 流体机械, 2003, 31(6): 11-14.

[2] 殷俊, 杨美传, 冯鉴. 基于热应力场耦合的涡旋压缩机动涡旋盘有限元分析[J]. 压缩机技术, 2011,(6): 6-9.

[3] 强建国, 刘振全. 基于稳态温度场轴向密封的涡旋齿高研究[J]. 润滑与密封，2007, 32(10): 62-65.

[4] Chiachin Lin, Yuchoung Chang, Kunyi Liang, et al. Temperature and Thermal Deformation Analysis on Scroll of Scroll Compressor [J]. Applied Thermal Engineering, 2005, 25:1724-1739.

[5] 王君, 张娜, 刘凯,等. 基于流场模拟的涡旋压缩机涡齿应力变形分析[J]. 工程热物理学报，2012, 33(8): 1134-1137.

[6] 黄蕾, 唐景春, 韩坤. 温度场对动涡旋盘应力与应变的影响[J]. 制冷技术，2013, 41(5): 60-63.

[7] Marco C.DINIZ, Evandro L.L.PEREIRA, Cesar J.DESCHAMPS. A Lumped Thermal Parameter Model for Scroll Compressors Including the Solution of the Temperature Distribution along the Scroll Wraps[C]. In: Proc. of International Compressor Engineering Conference. Purdue, 2012, 1341: 1-10.

[8] 张朝晖. ANSYS12.0热分析工程应用[J]. 北京：中国铁道出版社，2010.

Non-Uniform Orbiting Scroll Thermal Stress and DeformationAnalysis Based On Flow Field

LIU Tao, WANG Yongwei

(College of Mechanical and Electrical Engineering, Lan Zhou University of Technology, Lanzhou 730050, China)

The non-uniform orbiting scroll dimensional geometry is generated. The finite element model of its variable cross-section is established with the structural unit SOLID185. Then, the thermal load that is the surface temperature of the compressed working fluid and convective heat transfer coefficient is fitted for the load function. And the thermal analysis is done for the non-uniform orbiting scroll with the load. Compared with the analysis results of the thermal deformation and Mises stress of the scroll, it indicates that the simplified method of linear thermal load is reasonable, which can be used to analyze the deformation and stress of the scroll. And the finite element analysis based on the flow field is more suited for the actual working conditions of the scroll compressor.

compressor; orbiting scroll; variable cross-section; flow filed; thermal stress; thermal deformation

国家自然科学基金(51265027)；甘肃省高等学校基本科研业务费项目(1302ZTC034)

刘涛(1971-)，女，甘肃武威人，教授，博士，研究方向：机械设计及理论。

TH45

A

1671-5276(2015)05-0011-04

2014-03-20