钢纤维-钢筋混凝土板抗低速冲击作用机理研究

□□ 秦 菱，王鹏飞，童云罡

(1.空军勤务学院，江苏 徐州 221000；2.空后机营部，北京 100720；3.空后直供部 机场营房处，北京 100350)

工程应用

钢纤维-钢筋混凝土板抗低速冲击作用机理研究

□□ 秦 菱1，王鹏飞2，童云罡3

(1.空军勤务学院，江苏 徐州 221000；2.空后机营部，北京 100720；3.空后直供部 机场营房处，北京 100350)

主要从纤维强化理论、板壳理论和防护结构计算理论等3个方面，分别阐述了钢纤维-钢筋混凝土板构件在低速冲击作用下的强化原理，重点解释了钢纤维的增韧机理、薄板小挠度弯曲理论和弹性体系结构的动力分析方法。

钢纤维-钢筋混凝土；低速冲击；增强机理

引言

混凝土本身是一种脆性材料，十分有限的抗拉性能和极易发生脆性破坏的特点制约了其在工程领域的发展。在受拉部位配钢筋可以有效地提高混凝土结构的抗拉能力，钢纤维对混凝土韧性的增强已经受到工程界的广泛重视。本文就钢纤维-钢筋混凝土板抗低速冲击作用机理进行探讨。

1 纤维强化理论

钢纤维混凝土的增强机理主要有3种方式，分别是阻裂、增强和增韧。其中，钢纤维对混凝土最突出的改变在于对其韧性的显著改善[1]。钢纤维混凝土在基体发生开裂时仍能保持一定抗力的变形能力，一般用σ-ε曲线的有关面积参数来表示。纤维强化理论中最为重要的是纤维间距理论和复合材料力学理论。

1.1 纤维间距理论

纤维间距会影响混凝土的抗拉强度。纤维强化理论基于线弹性断裂力学，认为混凝土内部存在孔隙和微裂缝，在外力作用下会产生较大的应力集中，使裂缝进一步扩展，最终导致混凝土的破坏。钢纤维的加入使复合材料结构在成型和受力的过程中，其内部裂缝的产生和扩展得到了有效减少和限制，达到了钢纤维混凝土增强与增韧的效果。钢纤维混凝土的抗拉强度可表示为：

(1)

式中：K1c———钢纤维混凝土临界应力强度因子；Y———与裂缝形状有关的常数；K———与K1c、Y有关的常数；s———定向长纤维平均间距；a———裂缝半宽度。

1.2 复合材料理论

根据复合材料力学混合原理，钢纤维混凝土的弹性模量和强度性能遵循复合结构内部各组成部分性能的弹性叠加法则。其基本假定为：①基体混凝土为各向同性的匀质材料；②钢纤维沿受力方向平行、均匀分布；③钢纤维的变形与基体混凝土一致，无相对滑动产生。依据弹性叠加原理有：

(2)

σfc=σfρf+σmρm=σfρf+σm(1-ρf)

2 薄板小挠度弯曲理论

一般将板厚小于中面最小尺寸1/5的板称为薄板，将垂直于中面使薄板发生弯曲的力称为横向力，因此产生的应力应变可以按照薄板弯曲理论来解决[2]。薄板弯曲理论的基本假设为：①变形前垂直于中面的直线在变形后仍为直线，并垂直于变形后中面，其长度也保持不变；②对垂直于中面而产生的挤压应力可以忽略不计；③中面上点的位移都不平行于x、y方向。通过列举薄板的几何方程、物理方程、平衡方程和边界条件可以得到挠度函数：

(3)

式中：w———板的挠度；a，b———矩形板的边长；Amn———与振型相关的动力函数，m、n均为正整数。

针对本文重点研究的简支薄板，其挠度值的求解主要有纳维解法和李维解法。

2.1 四边简支矩形板的纳维解法

联立弹性曲面的微分方程和挠度函数，依据四边简支的矩形板的边界条件，以受均布荷载为例的薄板挠度有：

(4)

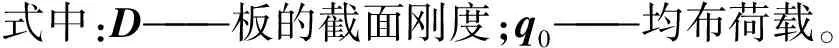
(m=1，3，5，…，n=1，3，5，…)

纳维解法适用于各种荷载，且级数的运算都较简单；缺点是只适用于四边简支的矩形薄板，且级数收敛较慢，较高的精度需要取级数的很多项。

2.2 矩形薄板的李维解法

对于有两个对边为简支的矩形薄板可用李维解法。将w表示成如下的单三角级数：

(5)

式中：Ym(y)———y的任一函数，m为任意正整数。

将边界条件带入(5)式，对于正方形板来讲，b=a，通过解微分方程可以得到李维解法的挠度表达式：

(6)

在级数中仅取前两项即能得到精确的答案。用李维解法解矩形板弯曲问题时，适用多种边界条件，但计算较为繁琐，不如纳维解法处理起来简单易行。

3 弹性体系结构的动力分析理论

在防护结构计算理论中将动力定义为：施加在结构上的随时间迅速改变方向、大小或位置的荷载，同时结构的内力和位移也跟随发生改变[3]。普遍是采用将结构视作弹性体系的方法进行动力分析。其基本原理是利用简化的结构单自由度体系将运动方程用常微分方程表示出来，从而得到结构体系的形变和位移规律。对于不同的研究对象，建立动力体系的运动方程主要有直接平衡法和能量法。

3.1 直接平衡法

结构在动力荷载作用下未发生变形，结构内部产生的与这一变形对应的内力就是抗力。根据牛顿第二定律有：

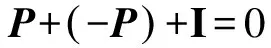
(7)

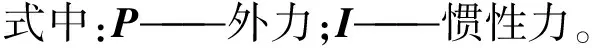
式中：P———外力；I———惯性力。

与静力平衡方程相比，(7)式仅增加一项惯性力I，把惯性力计入在全部力系内即可将动力问题按照静力问题的方式来处理。

3.2 能量法

能量法基于能量守恒原理，结构在动力荷载作用下不断积累应变能，任意时刻外力所做功与该时刻结构应变能和动能之间有如下关系：

(8)

W=U+K

与静力问题相比，(8)式中仅增加一项动能。若为自由振动，则外力功的一项等于常量。引入动力系数表示动载对结构作用的动力效应，即最大动挠度与将动载最大值当作静载作用下的静挠度的比值，则最大挠度可以表示为：

(9)

ydm=Kd·ycm

从而可以将动力荷载问题转换为静载作用下的问题予以解答。而动力系数的求解可以借鉴防护结构计算领域经典的动荷载模型，对于低速冲击作用来讲，动荷载可以看作是短时间作用的荷载，此时作用时间很小，动载系数可以表示为：

(10)

式中：ω———等效体系的自振频率，ω=KeMe，Ke为等效体系的弹簧常数；t1———荷载作用时间。

[1] 黄承逵.纤维混凝土结构[M].北京：机械工业出版社，2004：149-150.

[2] 成祥生.应用板壳理论[M].济南：山东科技出版社，1989：32-35.

[3] 王年桥.防护结构计算原理与设计[M].南京：工程兵工程学院出版社,1998：86-90.

(英文摘要

(编辑 芋艳梅)

Reinforcing Mechanism of Steel-Fiber-Reinforced Concrete Slabs against Low Speed Impact

QIN Ling1，WANG Peng-fei2，TONG Yun-gang3

(1.Air Force Service College，Xuzhou，Jiangsu，221000，China；2.The Airport Barracks Department of Air Force Service，Beijing，100720，China；3.The Airport Barracks Department of the Supply Ministry of Air Force Service，Beijing，100350，China)

This paper illustrates the reinforcing mechanism of steel-fiber-reinforced concrete slabs against low speed impact from the fiber reinforcing theory，the theory of plates and shells，and the protective structure calculation theory.It mainly explains the reinforcing mechanism of steel fiber，small deflection bending theory of thin slabs and dynamic analysis theory of elastic system structure.

steel-fiber-reinforced concrete；low speed impact；reinforcing mechanism

1009-9441(2015)05-0024-02

TU 528.572

A

秦菱(1990-)，男，四川眉山人，硕士研究生，研究方向为机场防灾减灾与防护工程。

2015-09-12