有限栈的出栈序列计数问题分析

王文龙

(喀什师范学院信息工程技术系， 新疆喀什 844000)

有限栈的出栈序列计数问题分析

王文龙

(喀什师范学院信息工程技术系， 新疆喀什 844000)

出栈序列个数是栈研究的基本问题.目前的研究大都基于无限栈，即不考虑栈空间的大小来讨论出栈序列计数问题.但在现实应用中，栈大小往往是有限的，出栈序列问题就要复杂得多.从非降路径计数的角度，分析了无限栈和有限栈的出栈序列计数问题；从二元函数的角度，给出了出栈序列计数的算法;最后设计出相应的程序进行实现和验证.实验证明，算法结果正确，算法设计易于理解.

有限栈；出栈序列；非降路径

栈是限定仅在表尾端进行插入或删除操作的特殊线性表.通常称表尾端为栈顶，向栈中插入元素称为进栈，从栈中删除元素称为出栈.由于插入和删除运算仅在栈顶一端进行，因此栈具有后进先出的特性，这种特性使得栈有着十分广泛的应用.对一个给定的入栈序列，文献[1-9]对出栈序列的数量等问题进行了研究.然而，以上研究结果均基于无限栈的前提，即栈的大小是不受限制的，也就是栈的大小大于等于入栈序列的长度.而在某些情况下，栈的大小会受到限制，即栈的大小小于入栈序列的长度，此时有限栈的入栈出栈问题会变得较为复杂.因此，文中从非降路径的角度，在栈大小不受限制和栈大小受限制两种情况下，对出栈序列计数问题进行分析研究，并给出计算算法和实现程序.

为方便分析，将研究的有关栈的问题描述为：给定入栈序列(1,2,…,n)，求出栈序列数量.

1 栈大小不受限制情况下非降路径的出栈序列计数

栈大小不受限制的出栈序列的计数，有多种方法[1-9],文中着重从非降路径计数[10]的角度分析出栈序列的计数问题.

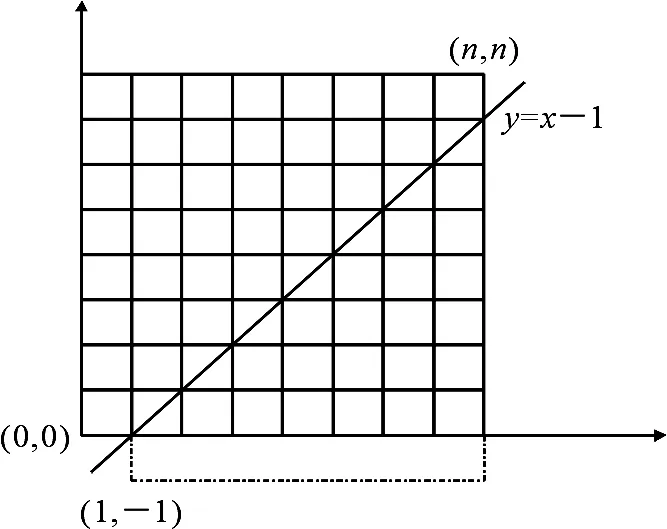
图1 上三角计数Fig 1Count of upper triangular

不妨设栈长度为入栈序列长度n，此时所有出栈序列的计数，可以用非降路径的计数解决.图1中，若将上行一步看做入栈一个元素，将右行一步看做出栈一个元素，则所有出栈序列的计数等于上三角中从(0,0)到(n,n)的非降路径总数.

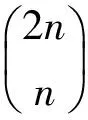
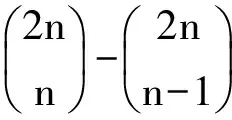
2 栈大小受限制情况下非降路径的出栈序列计数

为方便后续计算，需要先做如下2个计数.

2.1 计数1

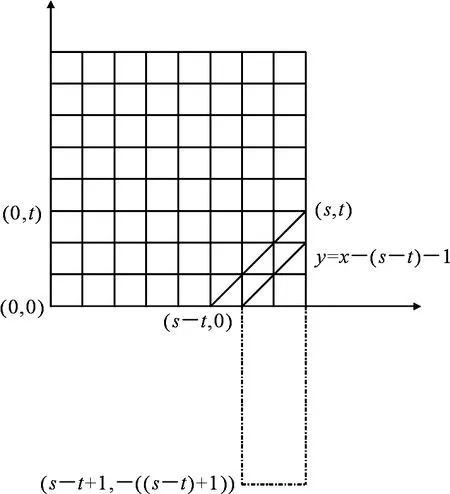
图2 直角梯形计数Fig 2Count of right angle trapezoid

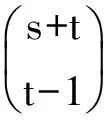
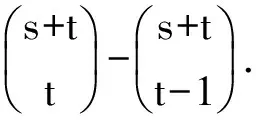
2.2 计数2

考虑计算图3由(0,0),(t,t),(s,t),(s-t,0)所组成的平行四边形中，从(0,0)到(s,t)的非降路径总数.

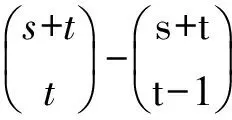
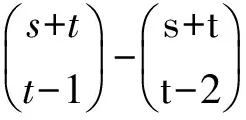
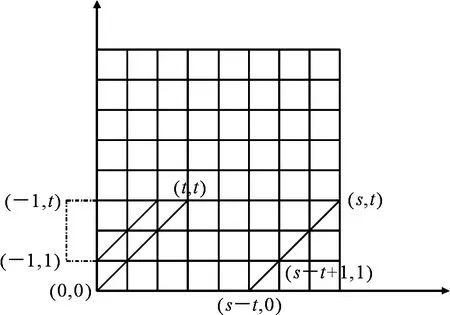
图3 平行四边形计数Fig 3Count of paralleogram

因此，由(0,0),(t,t),(s,t),(s-t,0)组成的平行四边形中，从(0,0)到(s,t)的非降路径总数等于

即

2.3 栈大小受限制的出栈序列计数

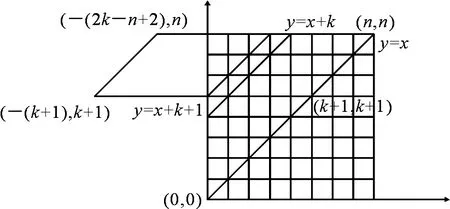
当栈的大小为k，小于入栈序列长度n时，栈中元素不能超过k个，则出栈序列的计数对应于图4上三角中从(0,0)到(n,n)不穿过y=x+k上点的非降路径数，即图4上三角中从(0,0)到(n,n)被y=x和y=x+k所夹的非降路径总数.

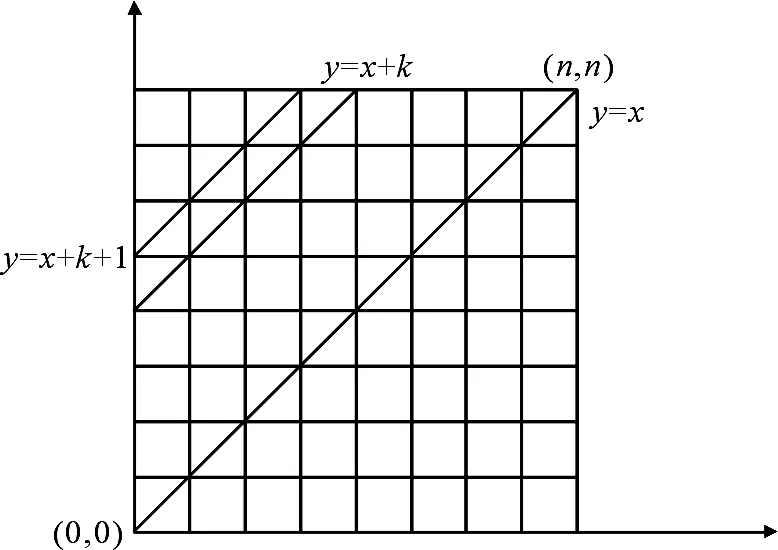
图4 被y=x与y=x+k所夹的计数Fig 4Count between y=x and y=x+k

现需计算上三角中从(0,0)到(n,n)接触(含穿过)y=x+k+1上点的非降路径总数.为求其值，结合非降路径的特点，在图5中，可以考虑求出接触(含穿过)a1点的非降路径总数、不接触a1点而接触(含穿过)b1点的非降路径总数……依次类推,直到求出不接触d1点之前的点而接触(含穿过)d1点的非降路径总数，然后将所求的非降路径总数求和，即为上三角中从(0,0)到(n,n)接触(含穿过)y=x+k+1上点的非降路径总数.

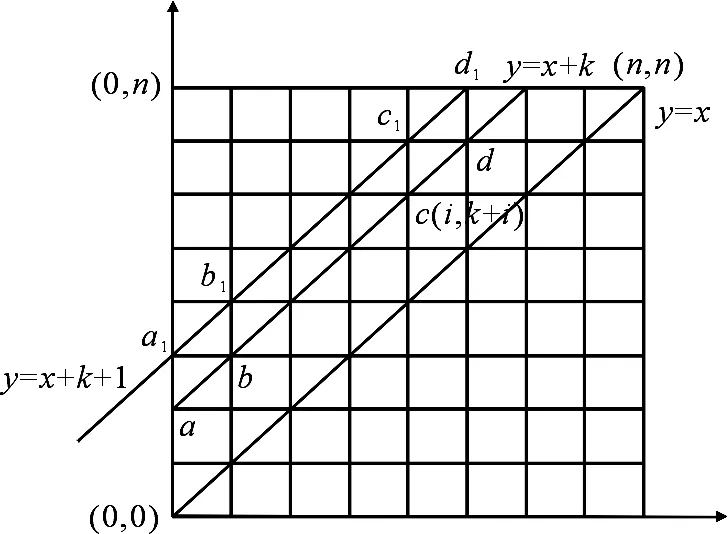
图5 接触y=x+k+1的计数Fig 5 Count of contact y=x+k+1

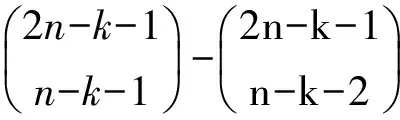
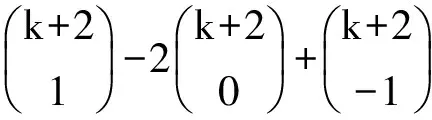
不接触c1点之前点而接触(含穿过)c1点的非降路径总数为这两部分之积

该式可化简为

根据以上分析，上三角中从(0,0)到(n,n)被y=x和y=x+k所夹的非降路径总数为

此值即为当栈的大小为k，小于入栈序列长度n时，出栈序列的计数.

2.4 几种特殊情况下的计数

2.3节中所得计数公式较为复杂，可以考虑以下几种较特殊的情况下的计数问题.

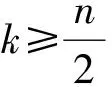
图的计数

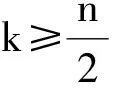
则上三角中从(0,0)到(n,n)被y=x和y=x+k所夹的非降路径总数为

此式可以化简为

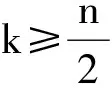
分析上式，当k=n-1时，值为

当k=n-2时，值为

2)当k=1时,不难发现出栈序列只有一种.

3)当k=2时,出栈序列的计数对应于图7上三角中从(0,0)到(n,n)被y=x和y=x+2所夹的非降路径总数.

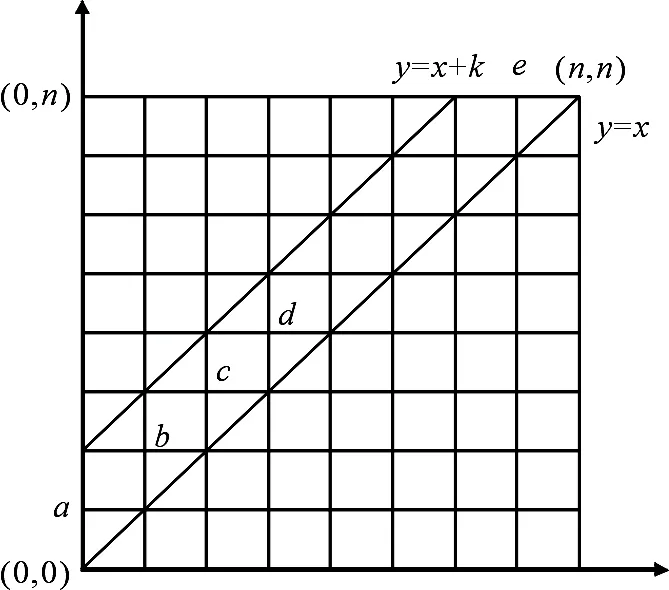
图7 被y=x与y=x+2所夹的计数Fig 7Count between y=x and y=x+2

此时求非降路径总数，可以做如下考虑.所求的非降路径先由(0,0)到a，而后由a到b，再到c……直到e，最后由e到(n,n).由(0,0)到a只有1种选择，而a到b有2种选择，b到c有2种选择……到e有2种选择，e到(n,n)只有1种选择.根据乘法法则可知，上三角中从(0,0)到(n,n)被y=x和y=x+2所夹的非降路径总数等于2n-1，此即当k=2时，栈大小受限时的出栈序列的计数.

3 计算算法及程序实现

为更好地计算出栈序列数量，从求二元函数值的角度，设计两种情况下出栈序列计数的算法及改进算法，并给出相应的程序实现.

3.1 栈大小不受限制

可以把问题描述为求一个二元函数f(x,y)的值，其中x表示待入栈元素个数，y表示已在栈中元素个数.对栈的操作不外乎两种：继续入栈一个元素，则此时待入栈元素个数变为x-1，栈中元素个数变为y+1；出栈一个元素，则此时待入栈元素个数不变为x，栈中元素个数变为y-1.用函数表示为f(x,y)=f(x-1,y+1)+f(x,y-1).

再考虑x=0和y=0两种特殊情况.当x=0时，则元素都在栈中，此时出栈序列数量为1，即f(0,y)=1；当y=0时，栈中无元素，此时只能入栈一个元素，待入栈元素个数为x-1，栈中元素个数为1，即f(x,0)=f(x-1,1).

此时，所求问题变为求函数f(n,0)的值.根据以上分析，可采用递归函数解决计数问题.程序如下：

#include“iostream.h”

intstacknum(intx,inty)

{if(x==0)return1;

if(y==0)returnstacknum(x-1,1);

returnstacknum(x-1,y+1)+stacknum(x,y-1);}

void main()

{ intx,y;

cout<<“please inputxandy:”<

cin>>x>>y;

cout<

考虑到递归效率不高，可以对程序进行改进.用二维数组s[i][j]来记录函数f(i,j)的值，则s[i][j]=s[i-1][j+1]+s[i][j-1].而当i=0时，s[0][j]=1;当j=0时，s[i][0]=s[i-1][1].由此可以得到如下效率更高的程序：

#include “iostream.h”

#defineN100

void inits(intx,ints[N][N])

{ inti,j;

for(i=0;i<=x;i++)

for(j=0;j<=x;j++)

{ if(i==0)s[i][j]=1; else if(j==0)s[i][j]=s[i-1][1];

else s[i][j]=s[i-1][j+1]+s[i][j-1];}}

void main()

{ intx,y,s[N][N]; cout<<“please inputxandy:”<

cin>>x>>y;

inits(x,s);

cout<

3.2 栈大小受限制

假设栈的大小为k，由3.1节可知，当y

可采用递归函数解决计数问题，程序如下：

#include “iostream.h”

intk;

long stacknum(intx,inty)

{ if((x==0)&&(y<=k)) return 1L;

if(y==0) return stacknum(x-1,1);

if(y==k) return stacknum(x,y-1); return stacknum(x-1,y+1)+stacknum(x,y-1);}

void main()

{ intn,m;

cout<< “please inputxyandk:”<

cin>>x>>y>>k;

cout<

亦可用二维数组记录函数值，程序如下：

#include “iostream.h”

#defineN100

intk;

void inits(intx,int s[N][N])

{ inti,j;

for(i=0;i<=x;i++)

for(j=0;j<=k;j++)

{ if(i==0)s[i][j]=1; else if(j==0)s[i][j]=s[i-1][1]; else if(j==k)s[i][j]=s[i][j-1]; elses[i][j]=s[i-1][j+1]+s[i][j-1];}}

void main()

{ intx,y,s[N][N];

cout<<“please inputxyandk:”<

cin>>x>>y>>k;

inits(x,s); cout<

[1] 张先伟,曹雁锋.用插入法解决堆栈输出问题[J].计算机应用与软件,2007,24(11):169-171.

[2] 唐锐.用后继序列法解决堆栈输出问题[J].小型微型计算机系统,2006,27(12):2314-2316.

[3] 徐凤生.出栈序列的性质及其求解新算法[J].计算机工程与应用,2006,42(5):66-68.

[4] 何坤金,陈正鸣,杨垠.基于算子的栈序列生成算法与实现[J].计算机工程与设计,2006,27(12):2266-2267.

[5] 唐保祥.栈序列及其生成算法[J].郑州大学学报:自然科学版,2001,33(4):33-35.

[6] 李红卫,徐亚平.出栈序列的研究[J].计算机技术与发展,2007,17(10):127-129.

[7] 袁红娟.基于链表的出栈序列生成算法[J].河北北方学院学报:自然科学版,2006,22(5):71-75.

[8] 韩静.“数据结构”课程中出栈序列的一种求解算法[J].计算机教育,2008,6(23):68-70.

[9] 吴集林.用二叉树解决出栈序列问题[J].赣南师范学院学报:自然科学版,2005,26(6):28-30.

[10] 卢开澄,卢华明.组合数学[M].第4版.北京：清华大学出版社,2006:128-130.

(责任编辑 惠松骐)

Analysis of counting problems on limited stack-output

WANG Wen-long

(Department of Information Engineering and Technology,Kashgar Teachers College,Kashgar 844000,Xinjiang,China)

The stack-output number is a basic problem of stack research.The present research is mostly based on infinite stack,which does not consider the size of the stack,and the stack-output counts are discussed.But in the practical applications,the size of stack is often limited,the stack-output problem has much more complexity.From the perspective of the counting on not descend path,counting problem of limited stack and infinite stack on stack-output is analysed.And from the perspective of dual function,algorithms are designed.Finally the corresponding programs are designed and verified.The results show that the algorithm is correct,and the algorithm design is easy to understand.

stack;limited stack;stack-output;not descend path

2014-10-23;修改稿收到日期:2015-01-17

新疆自治区高校科研计划重点项目(XJEDU2014I039)；喀什师范学院教研教改重点项目(KJDZ1303,KJDZ1202)；喀什师范学院重点课题((13)2456)

王文龙(1976—)，男，湖南双峰人，副教授，硕士.主要研究方向为计算机软件与信息安全. E-mail:wwl-yx@163.com

TP 311

A

1001-988Ⅹ(2015)04-0046-06