地球自转对弹道导弹被动段落点的影响
苏 浩
(江苏自动化研究所,江苏连云港 222006)
弹道导弹的被动段主要受3 个因素的影响:地球自转、地球扁率、空气阻力。在弹道导弹诸元准备中,需分析这3个因素对被动段落点射程的影响及影响方式,以便采取相应的方法来提高诸元准备的速度和精度。对中、远程弹道导弹,地球自转是影响落点射程的最重要因素,第二位的是地球扁率,空气阻力的影响一般仅有几百米而已。温羡峤[1]、谢代华[2]在圆球地球模型上以椭圆弹道理论为基础分析了地球自转对弹道的影响,但这些分析存在着一定程度的不足,在较真实地球物理条件下分析探讨这一问题具有更为现实的意义和参考价值。本文以正常地球椭球体地球模型为基础,合理简化被动段运动微分方程,从动力学角度针对典型射击情况分析探讨地球自转对被动段落点射程的影响。
1 被动段运动微分方程及简化
1.1 被动段运动微分方程
弹道导弹的被动段运动通常以质点的动力学问题进行研究,导弹在被动段受空气阻力、地球引力、由地球自转产生的柯氏惯性力及牵连惯性力的作用,由质点的动力学理论,发射坐标系中的被动段动力学矢量方程为[3]
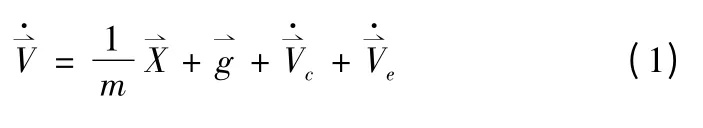

式(1)、式(2)组成被动段弹道运动微分方程组,其为变系数非线性常微分方程组,当给定初始参数,采用数值方法积分,便可求得被动段弹道参数。
1.2 运动微分方程的简化
弹道导弹的被动段由自由段和再入段两部分组成,导弹在自由段的射程和飞行时间占全弹道的80% ~90% 以上[4]。在自由段,导弹在相当稀薄的大气中飞行,空气阻力远远小于其他作用力,通常认为导弹是在真空中飞行的,不考虑空气阻力的影响;再入段就是导弹重新进入大气层直至落点的一段弹道,再入段的空气阻力对导弹的飞行速度有较大影响,而对导弹的射程及飞行时间的影响较小。为了便于分析地球自转因素对被动段落点射程的影响,同时又保证一定的计算精度,进行如下假设:
a)地球为正常地球椭球体,长半轴aE=6 378 140 m,扁率αE=1/298.257;
b)地球匀速自转,自转角速度Ω = 7. 292 115 ×10-5s-1;
c)忽略再入段空气阻力的影响。
综上几点所述,发射坐标系中被动段的标量方程组为
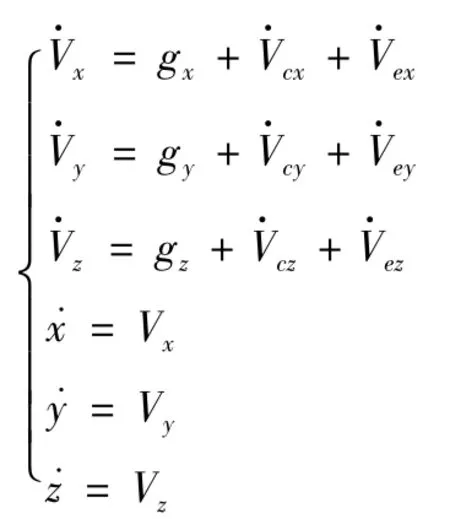
2 主要参数的计算
2.1 柯氏加速度的计算
由理论力学,式(1)中导弹的柯氏加速度为

依据矢量外积运算,柯氏加速度在发射坐标系各轴上的分量为
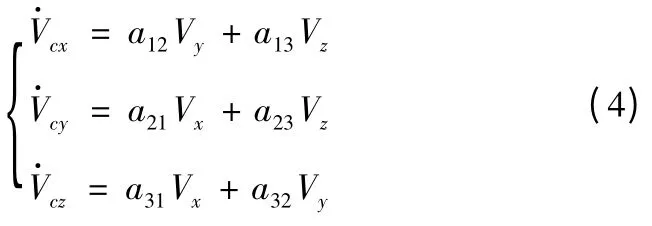
式中:
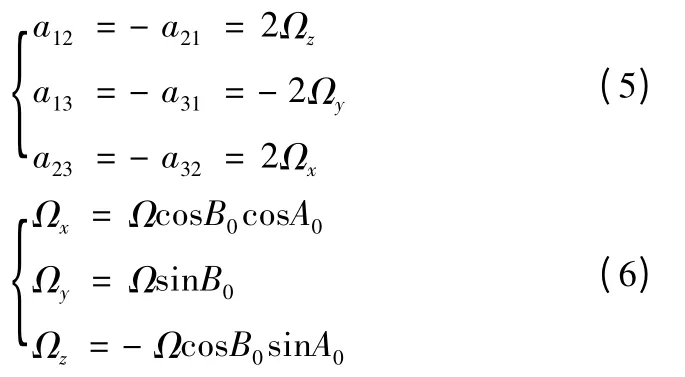
Ωi(i=x,y,z)为地球自转角速度在发射坐标各轴上的分量;B0为发射点地理纬度;A0为射向。
2.2 牵连加速度的计算
由理论力学,式(1)中导弹的牵连加速度为
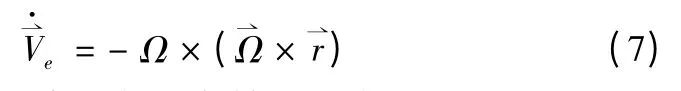
牵连加速度在发射坐标系各轴上的分量为
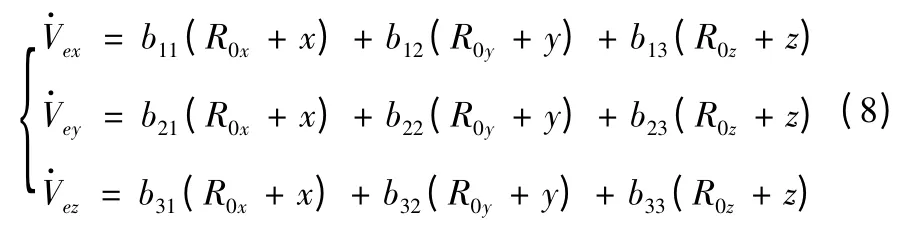
式中:
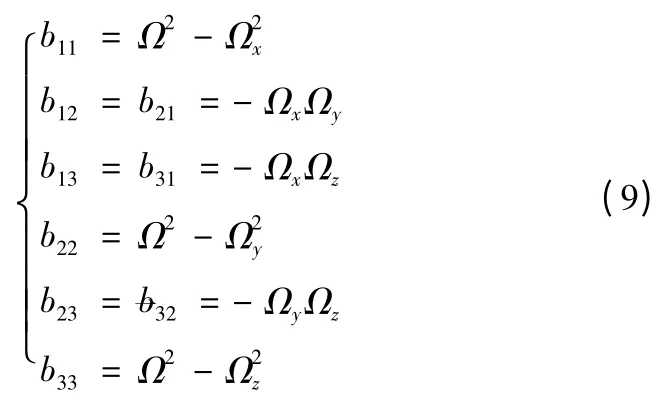
R0i(i=x,y,z)为发射点地心矢径在发射坐标系各轴上的分量为导弹的地心矢径。
2.3 落点纬度和经度的计算
2.3.1 落点纬度的计算
落点的地心纬度的计算式为
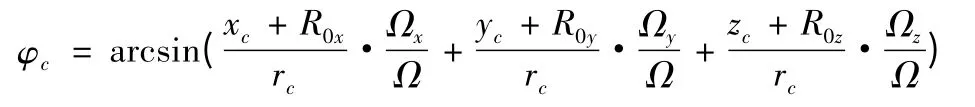
式中:为导弹落点位置在发射坐标系各轴上分量;rc为落点地心距。
地心纬度到地理纬度的转换公式为[5]
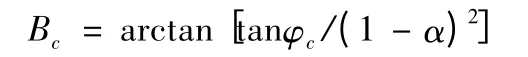
2.3.2 落点经度的计算
发射点与落点之间的经度差为
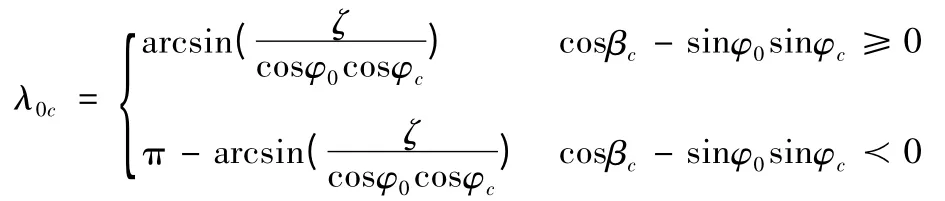
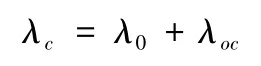
因此落点经度为
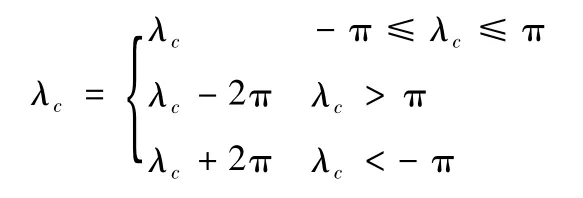
2.4 射程偏差和横向偏差的计算
在地球自转因素的作用下,导弹的落点将产生偏差(图1),C1为地球自转因素作用下导弹落点,C2为忽略地球自转因素导弹落点。C2在射击平面OC1OE内的投影点为C',C'与落点C1之间的距离ΔL 为射程偏差,C2与C'之间的距离ΔH 为横向偏差[3]。
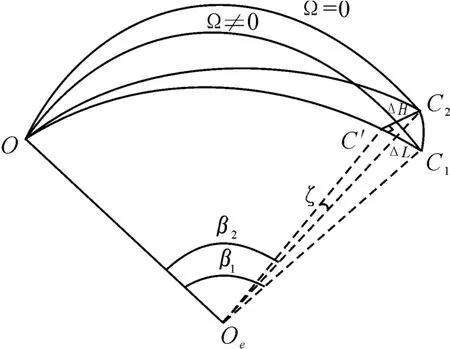
图1 落点偏差示意图
落点C1、C2的射程角为β1、β2,相对发射点的球面方位角为ψ1、ψ2,由球面三角形公式,可得:
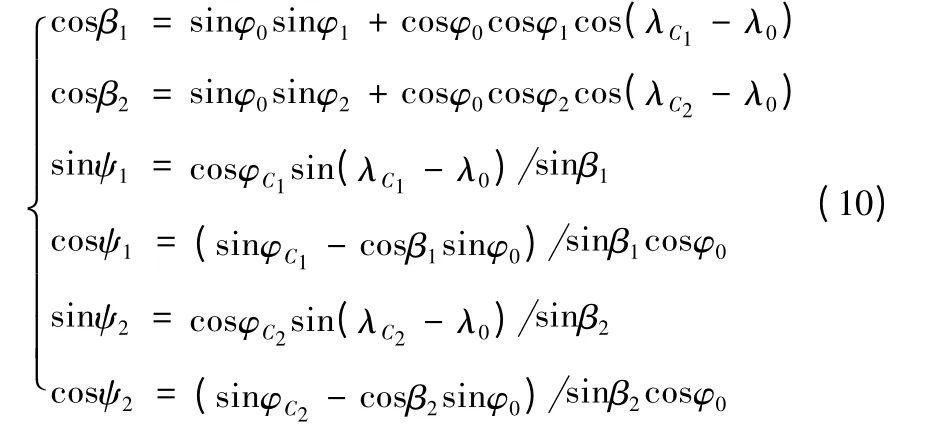
式中:φ0、φ1、φ2分别为发射点、落点C1、落点C2的地心纬度;λ0、λC1、λC2分别为发射点、落点C1、落点C2的经度。
射程偏差ΔL 的计算公式为
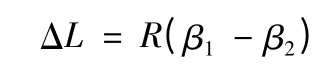
设ΔH 对应的地心角为ζ,则横向偏差为
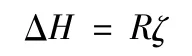
由球面三角形正弦定理

则有
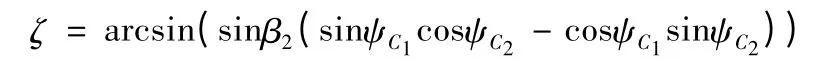
将式(10)的相关计算式代入即可求得ζ。
为计算出更精确的ΔL、ΔH,可用C'处的地心半径代替地球平均半径。
3 地球自转对被动段落点射程的影响分析
地球自转产生柯氏加速度和牵连加速度,使得导弹在被动段飞行中的受力发生改变,从而使得导弹的落点相对于地球静止时产生偏差。由式(3)可知,柯氏加速度的大小和方向由2决定,当主动段终点参数所决定的射击平面与赤道平面重合时,则柯氏加速度在赤道平面内,使得弹道参数发生变化,造成射程偏差,但不会造成横向偏差。除上述情况外,柯氏加速度作用的结果既会产生射程偏差也会产生横向偏差,计算结果如表1 所示。
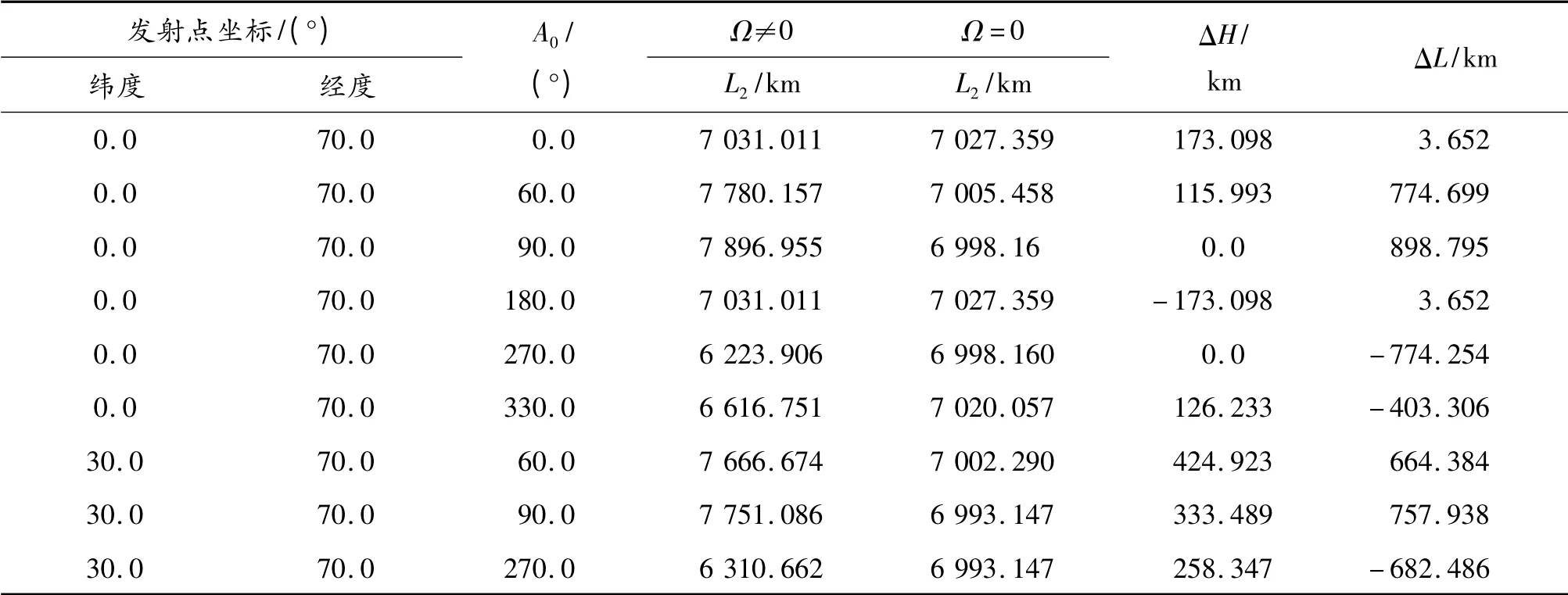
表1 柯氏加速度对落点射程的影响
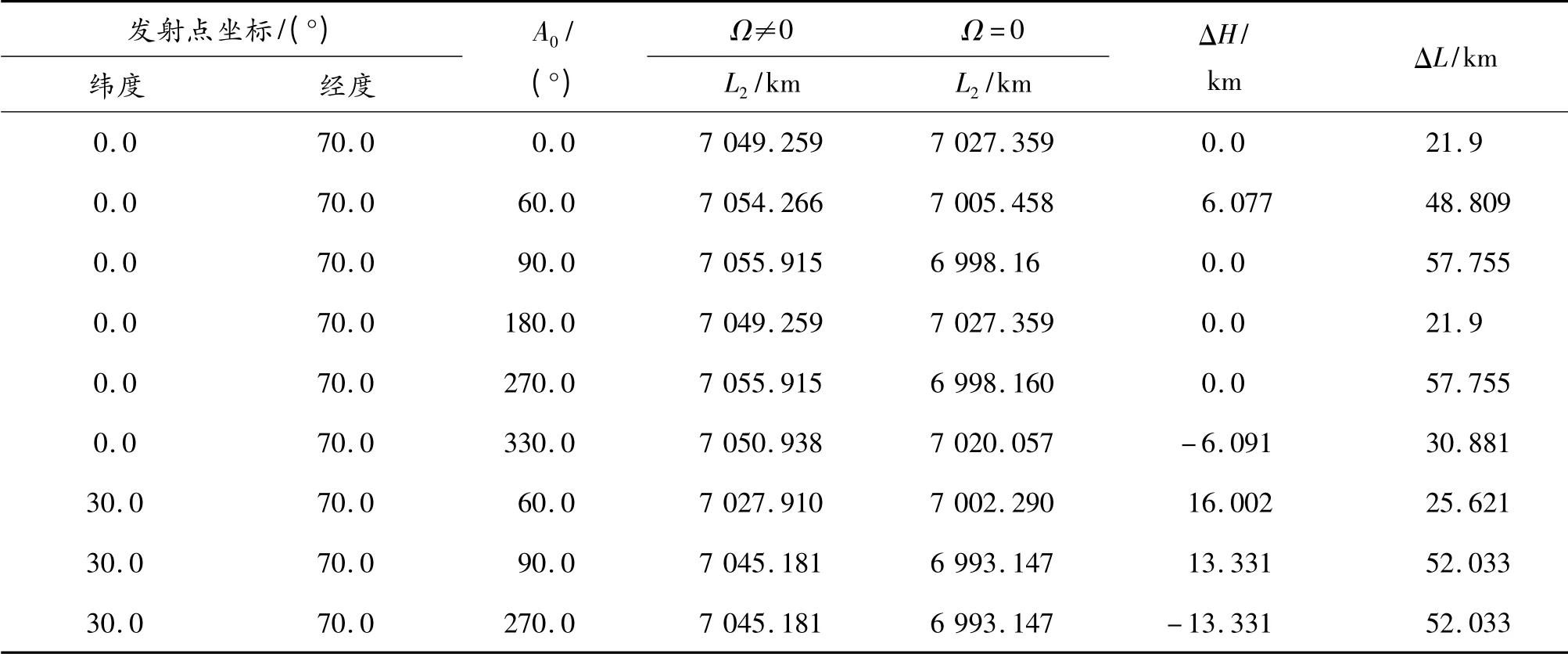
表2 牵连加速度对落点射程的影响
计算结果表明,在地球自转因素的作用下,当导弹向东射击时,射程将增加,向西射击时,射程将减小。下面以导弹发射点位于赤道,主动段弹道终点参数所决定的射击平面与赤道平面重合这种典型的射击情况展开分析。
3.1 柯氏加速度对落点射程的影响
导弹向东射击,B0=0°,A0=90°,由式(5)、式(6)可得
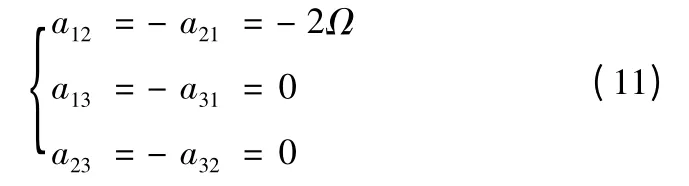
将式(11)代入式(4),有
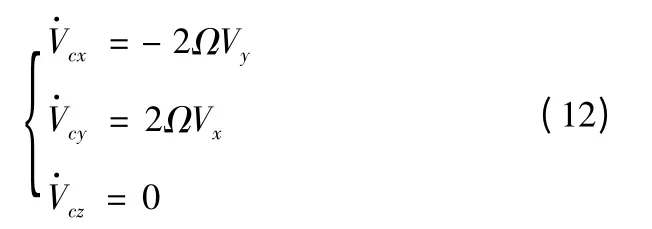
导弹向东射击时,速度分量Vy在被动段开始飞行不长的一段时间内由正值减小到零,此后Vy为负值且绝对值不断增大,由式(12)第一式可知,柯氏加速度分量在被动段开始的一段时间内为负值逐步到零,此后为正值,且不断增大;速度分量Vx在被动段飞行的绝大部分时间内为正值,只有在落点前一段不长的时间内才有可能为负值(射程较大时才会出现负值的情况),由式(12)第二式,柯氏加速度分量被动段飞行的绝大部分时间内为正值,只有在落地前一段不长的时间内才有可能为负值。从导弹整个被动段的飞行来看,导弹向东射击时,柯氏加速度总作用的结果将使得弹道高度提高、射程增加,仿真计算结果见表1,图2 给出了导弹向东射击,在Ω=0 射程约为7 000 km 时随飞行时间的变化曲线。
导弹向西射击,B0=0°,A0=270°,由式(5)、式(6)可得
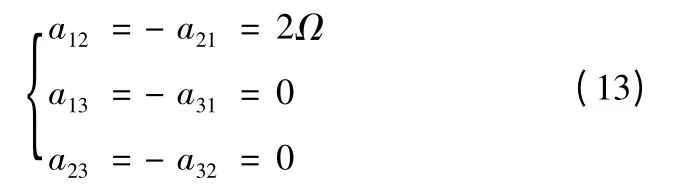
将式(13)代入式(4),有
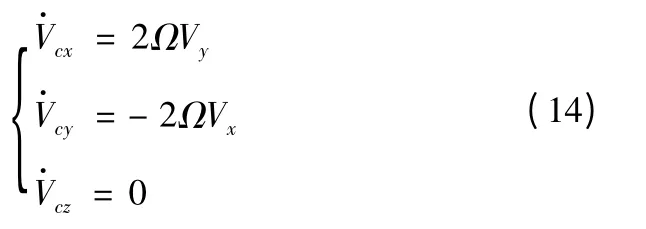
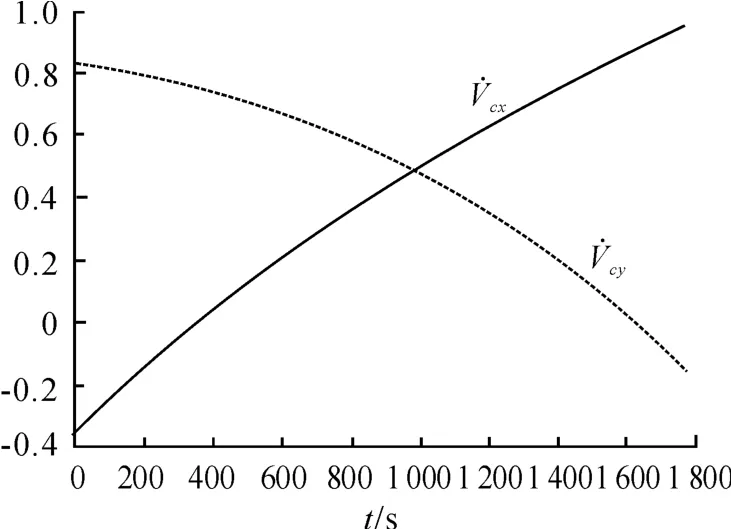
图2 随飞行时间变化曲线
导弹向西射击时,速度分量Vy在被动段开始飞行不长的一段时间内由正值减小到零,此后Vy为负值且绝对值不断增大,由式(14)第一式可知在被动段开始的一段时间内为正值逐步到零,此后为负值且绝对值不断增大;速度分量Vx在被动段飞行的绝大部分时间内为正值,只有在落地前一段不长的时间内才有可能为负值,由式(14)第二式,柯氏加速度分量在被动段飞行的绝大部分时间内为负值,只有在落点前的一段时间内才有可能为正值。从整个被动段的飞行来看,导弹向西射击时,柯氏加速度总作用的结果将降低弹道高度、减小射程,仿真计算结果见表1,图3 给出了导弹向西射击,在Ω=0 射程约为7 000 km 时,随飞行时间的变化曲线。
3.2 牵连加速度对落点射程的影响
由式(6)、式(9)可知,无论导弹向东射击,还是向西射击,均有
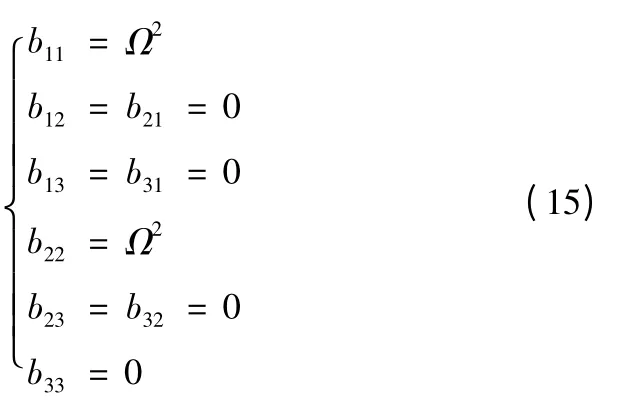
将式(19)代入式(8),有
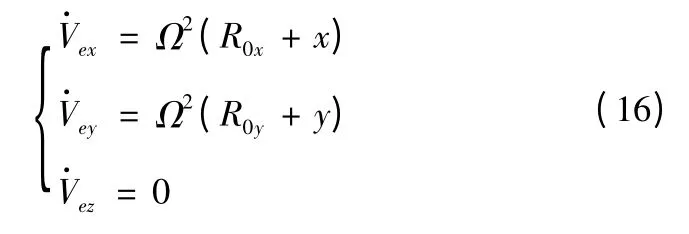
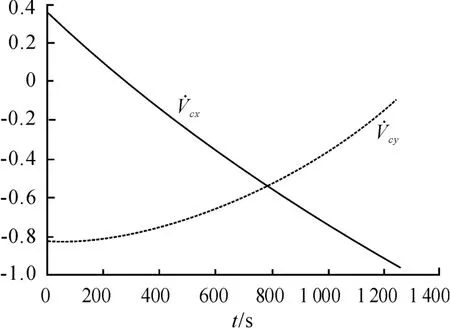
图3 随飞行时间的变化曲线
对于中、远程弹道导弹,在被动段飞行的整个阶段R0x+x、R0y+y 均为正值,由式(16)可知在被动段飞行的整个阶段为正值,因此,牵连加速度的作用将使得弹道高度提高,射程增加,仿真计算结果见表2,图4 为导弹向东射击,在Ω=0 射程约为7 000 km 时随飞行时间的变化曲线,图5 为导弹向西射击,在Ω =0 射程约为7 000 km 时,随飞行时间的变化曲线。
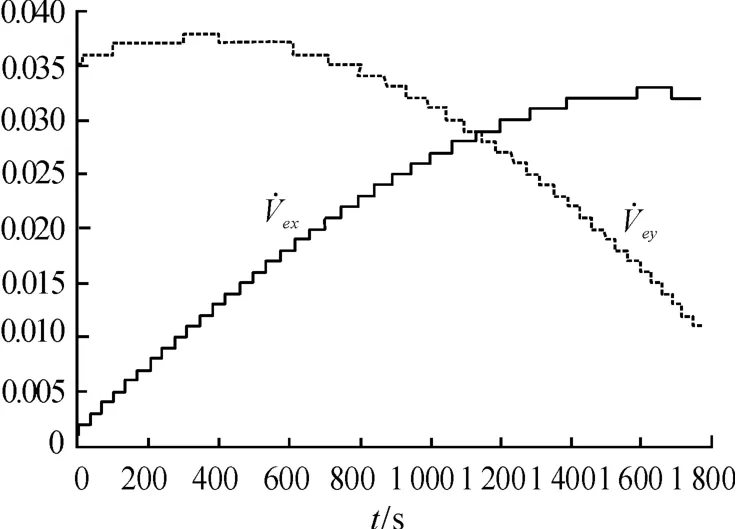
图4 随飞行时间的变化曲线
3.3 柯氏加速度与牵连加速度的综合作用
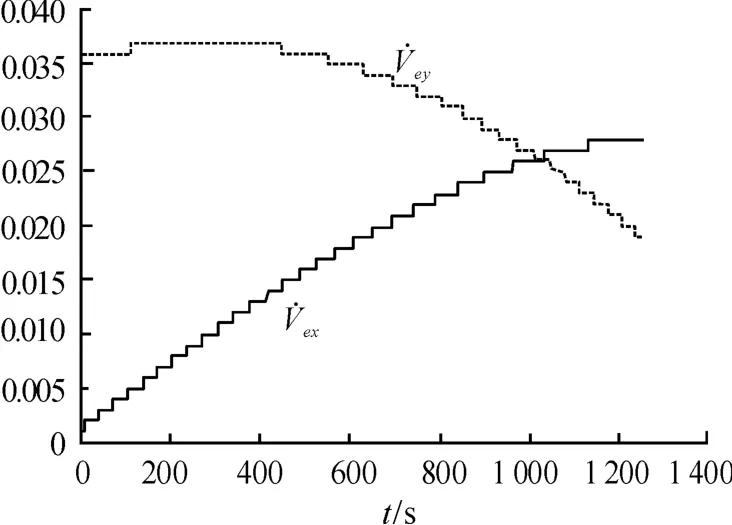
图5 随飞行时间的变化曲线
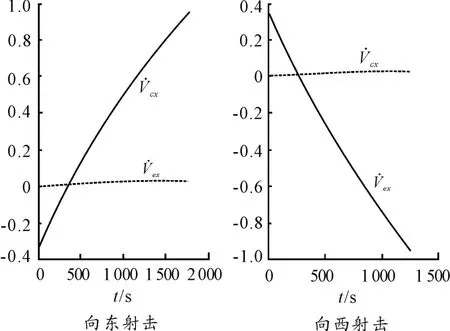
图6 随飞行时间的变化曲线
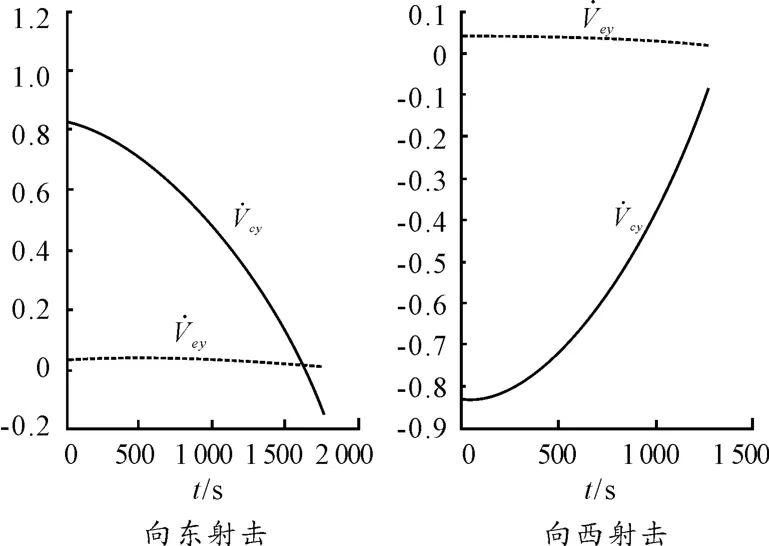
图7 随飞行时间的变化曲线
4 结束语
[1]温羡峤,高雁翎.地球旋转对弹道性能影响分析[J].现代防御技术,2006,34(1):11-15,36.
[2]谢代华.地球自转对弹道导弹轨道和落点影响分析[J].航空兵器,2006(1):18-21.
[3]张毅.弹道导弹弹道学[M].长沙:国防科技大学出版社,1998.
[4]贾沛然.远程火箭弹道学[M].长沙:国防科技大学出版社,1993.
[5]肖业伦.航空航天器运动的建模—飞行动力学的理论基础[M].北京:北京航空航天大学出版社,2003.

