基于有限时间同步的无人艇集结控制研究

徐 林，陈 云，桂志芳，刘 忠

(1.海军装备研究院，北京 100161; 2.海军工程大学 a.电子工程学院; b.兵器工程系，武汉 430033)

21 世纪以来，无人机在阿富汗战争、伊拉克等战争中，取得了巨大的军事效益。由此引发了世界各国对无人机、无人艇、水下无人航行器等无人作战平台的广泛关注，纷纷制定相关发展规划［1-2］，并投入了大量人力物力开展无人作战平台的相关技术研究［3-15］。近年来，无人机技术已经取得了跨越式发展［3-4］，水下无人航行器技术也得到了大量研究［5-11］。相对于无人机和水下无人航行器，无人艇的研究结果比较少见［12-15］。但另一方面，无人艇的应用无疑是十分重要的，比如使用无人艇遂行情报侦察、监视、目标攻击、反潜、防空等作战任务时，由于其目标小，机动性强，不易被敌人发现。在执行这些作战任务时，往往需要多艘无人艇进行协同，从而达到单艇所无法取得的作战效果。比如，在舰艇编队进入作战区域时，母舰可以释放多艘无人艇执行搜索敌潜艇的任务，当某一艘无人艇发现目标时，可以向其他无人艇发出信息，集体向目标位置集结，然后发起攻击，这样可以增大发现和摧毁敌潜艇的概率。因而分布在不同位置的无人艇的集结控制问题是一个值得研究的问题，但对这一问题的研究却未引起人们的足够重视。

众所周知，同步是指两个或多个系统，在外部驱动或者相互耦合的作用下，调整它们的某个动态性质以达到相同性质的过程［16］。按同步时间划分，同步可分为渐近同步［17-18］和有限时间同步［16，19-24］两种类型。值得注意的是，渐近同步只能保证系统在时间趋于无穷大时达到同步，而有限时间同步却能够保证系统在有限的时间内或尽可能短的时间内达到同步。显然，有限时间同步更切合实际应用。

为此，本文将基于有限时间同步理论，研究分布在不同位置的无人艇的集结控制问题。为简化模型，本章只考虑两艘无人艇的集结问题。同时由于各无人艇集结时的位置相距不远，且远小于初始分布时无人艇之间的距离，因而我们在建模时可以近似认为无人艇集结时的位置相同。

1 无人艇的运动模型

考虑如图1 所示的水面无人艇的平面运动。该艇由两个独立的推进器来产生推力和转向力。在图1 中，X -Y 为绝对坐标系(大地坐标系)。令 (x(t)，y(t))是无人艇在绝对坐标系上t 时刻的位置坐标，ψ(t)为无人艇在绝对坐标系上t 时刻的首向偏航角(表示无人艇的运动方向)。那么，无人艇在t 时刻的水平面运动状态可以由 (x(t)，y(t)，ψ(t))确定。建立原点G 在无人艇的重心处，且坐标轴与无人艇惯性主轴重合的运动坐标系(体坐标系)G -xByB。再令vx(t)和vy(t)分别为无人艇在t 时刻的线速度沿运动坐标系的横轴和纵轴方向的速度分量，ωz(t)为无人艇在t 时刻的(水平)旋回角速度。

图1 水平面坐标系下的水面无人艇［12］

由绝对坐标系和运动坐标系的关系容易得到如下等式［12］:

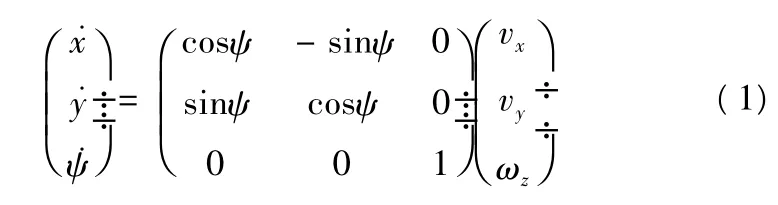
忽略风力和波浪力的影响，可以得到以下简单的动力学模型［12］:

其中，正常数mii(i =1，2，3)由无人艇的惯性和附加质量确定，正常数dii(i=1，2，3)为水动力衰减常数，τ1和τ2为推进器产生的外力。

进一步令m11=m22=m，d11=d22=d，可以得到以下简化模型:

通过式(1)可将式(3)转换到绝对坐标系，方程为

其中:

2 无人艇集结控制模型

不失一般性，本文只考虑两艘无人艇的集结问题。散布在不同位置的两艘无人艇，当其中一艘无人艇(作为主艇)发现目标时，在继续对目标进行跟踪的同时，持续不断地给另一艘无人艇(作为从艇)发送自身的状态信息，从艇接收到主艇的信息并传递给自身控制器，控制器根据主艇和从艇本身的状态信息产生控制信号给操纵系统，由其驱动从艇向主艇机动，直至与主艇的位置、运动方向、速度及加速度达到一致，完成集结，然后发动攻击。

根据式(5)，可采用如下主-从同步框架来实现两艘无人艇集结控制:

主艇和从艇的有限时间同步问题可描述为:设计一种合适的控制器U(X，Z)，使得对于主艇的初始状态X1(0)，和从艇的初始状态主艇和从艇的状态变量满足:

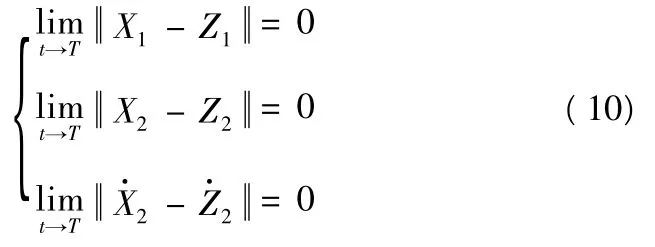
并且当t ＞T 时，

其中，有限正数T 为同步时间，‖·‖表示欧几里德范数。

因此，如果零点E =0 是误差系统式(12)的平衡点(此时有E1=0，E2=0，E3==0)，并且误差系统(12)在零点E=0 是全局有限时间稳定的，那么从系统(从艇)的位置、运动方向、速度和加速度与主系统(主艇)的相应状态变量达到全局有限时间同步。

现在，无人艇在有限时间内的集结问题可转化为: 设计一种合适的同步控制器U(X，Z)，使得对于主(主艇)-从(从艇)系统的主艇的任意初始状态X1(0)，X2(0)和从艇的任意初始状态Z1(0)，Z2(0)，误差系统式(12)在E=0 达到全局有限时间稳定。

3 集结判据

为了使从艇集结到主艇的位置，即误差系统式(12)在E=0 达到全局有限时间稳定，采用如下有限时间同步控制器——广义线性反馈控制器［9］:

其中，K1= diag{ k11，k12，k13，k14，k15，k16} ∈R6×6和K2=diag{k21，k22，k23，k24，k25，k26}∈R6×6为待定的常数耦合矩阵，

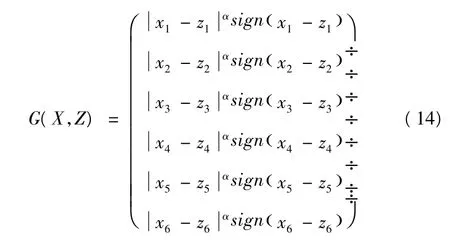
式(14)中:

注解1 值得注意的是，控制器(13)结构简单，实现成本低。此外，该控制器连续，不会产生抖振现象。而在同步过程中，系统的抖振可能会破坏同步［23］。

下面，我们来寻找合适的耦合矩阵K1和K2使得误差系统式(12)达到全局有限时间稳定。

由中值定理可知:

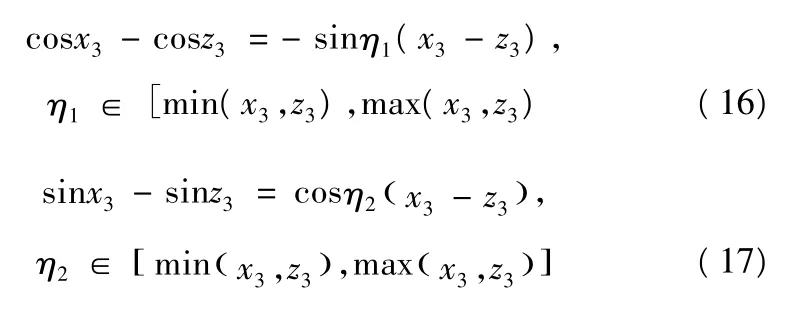
由式(16)和式(17)易得:

其中:

根据式(12)～(14)、式(18)和式(19)，可知:

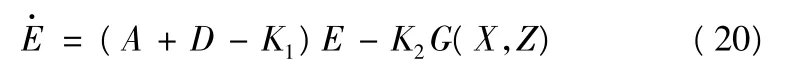
根据有限时间稳定性定理来证明两艘无人艇集结(同步)的条件。

定理1如果存在一个式(13)定义的控制器U(X，Z)，使得

则主-从无人艇可以集结到同一地点(达到全局有限时间同步)，且相应的集结(同步)时间满足:

其中c=min{k21，k22，…，k26}，E(0)=X(0)-Z(0)，α∈(0，1)。

证明:选择二次型Lyapunov 函数V(E)=ETE，则V(E)沿着误差系统(20)的轨迹对时间t 的导数为:

对于任意的α∈(0，1)，由附录A 引理2 有:

根据附录A 引理1，由式(21)、(23)和式(24)可知: 如果存在常数c=min{k21，k22，…，k26}，使得

则主-从无人艇可以集结到同一地点(达到全局有限时间同步)，同步时间T 满足不等式(22)。

证毕。

根据定理1，易证如下推论1。

推论1如果存在一个式(13)定义的控制器U(X，Z)，使得

则主-从无人艇可以集结到同一地点(达到全局有限时间同步)，且相应的集结(同步)时间满足:

其中c=min{k21，k22，…，k26}，E(0)=X(0)-Z(0)，α∈(0，1)。

证明:由式(6)和式(19)可知:

式(33)中:

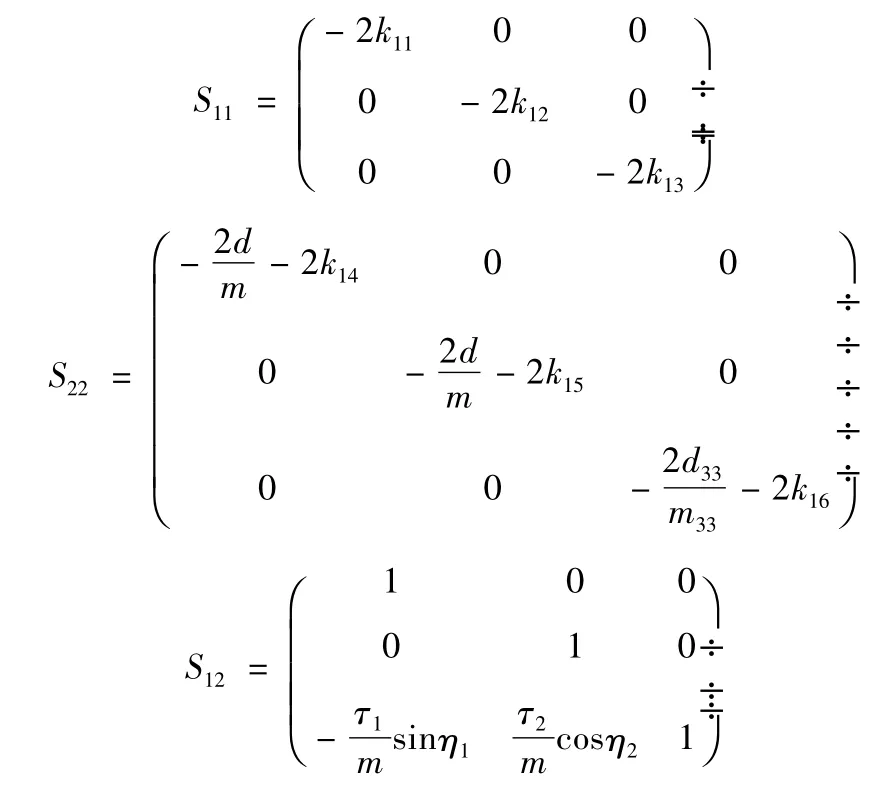
则由附录A 引理3 可知:S 负定，如果

显然，如果式(26)～式(28)成立，那么式(34)恒成立。

再次根据附录A 引理3 可知式(35)成立，如果

又由于sin2η1≤1，cos2η2≤1，如果式(29)～式(31)成立，那么式(36)～式(38)成立。

综上，根据定理1，该推论得证。

证毕。

4 数值仿真

下面通过一个例子来验证所得结果的有效性。选取无人艇的惯性和附加质量系数m =m11=m22=100，m33=120，水动力衰减常数d=d11=d22=12，d33=14，推进器产生的外力τ1=τ2=50。主从无人艇的初始值分别为X(0)=(12.1，2.6，3.5，2.3，2.1，2.7)T和Z(0)=(1.7，23.2，35.8，4.2，1.4，3.3)T，主从无人艇的状态轨迹如图2 ～图3 所示。根据推论1，选择控制器(13)中参数耦合矩阵K1=diag{0.1，0.3，0.2，34，0.6，1.4}，K2= diag{0.1，0.1，1.0，0.2，0.4，0.1}，则主-从无人艇可以集结到同一地点(即达到全局有限时间同步)，如图4 ～图6 所示。同时可以根据式(32)计算出相应的集结(同步)时间的估计值T*=174.7，如图4 ～图6 所示，实际同步时间T≤T*。由此可见，本文所得的结果是有效的。

图2 主无人艇的动力系统的轨迹

图3 从无人艇的动力系统的轨迹

图4 主无人艇和从无人艇位置及角度误差E1 =(e1，e2，e3)T 的轨迹

图5 主无人艇和从无人艇速度误差E2 =(e4，e5，e6)T 的轨迹

图6 主无人艇和从无人艇加速度误差的轨迹

5 结束语

本文应用有限时间同步理论，研究了无人艇的集结控制问题。基于无人艇的运动模型，构造了无人艇集结控制的模型，将集结控制问题转化为全局有限时间同步问题; 然后基于该模型，证明了在广义线性反馈控制下，主从无人艇集结(同步)的判据，并给出了集结(同步)时间的估计表达式。最后，通过数值实例验证了所得判据是有效的。本文采用的广义线性反馈控制器简单易行，同步成本低。由推论1 可以看出，本文所得到的判据简洁直观，代入系统参数即可判断无人艇是否可以集结到同一地点，还可以根据式(32)对同步时间进行估计。

附录A(Appendix A)

考虑如下系统:

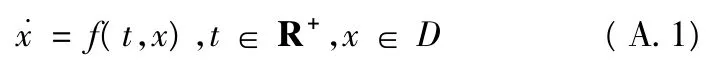
其中，f:R+×D→Rn是连续函数，且f(t，0)=0 对任意t≥t0都成立，即原点是系统(A.1)的一个平衡点。

引理1［25］如果存在一个连续可微的正定函数V: D→R、实数β ＞0 和实数α∈(0，1)以及一个原点的开邻域U⊆D，使得

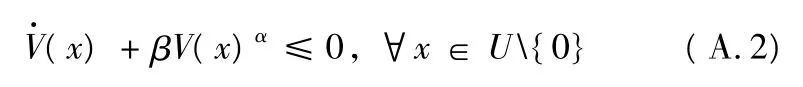
那么系统(A.1)在原点是有限时间稳定的，并且停息时间函数满足

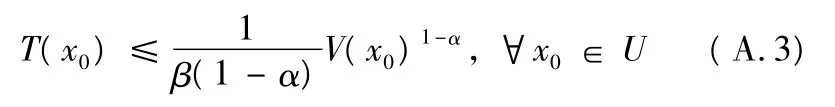
其中，x0是变量x 的初始值.

另外，如果D =Rn，V 是径向无界的，那么系统(A.1)是全局有限时间稳定的。

引理2［26］对任意正实数αi，i=1，2，…，n 和0 ＜p ＜2，下面的不等式成立:

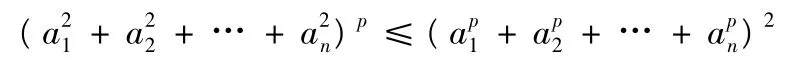
引理3［27］对给定的对称矩阵其中S11∈Rr×r，那么下面的3 个条件是等价的:

(1)S ＞0(＜0);

［1］DOD.The navy UUV master plan［R］.American，November，2004.

［2］DOD. Unmanned aircraft systems roadmap 2005—2030［R］.American，July，2004.

［3］Austin R.Unmanned aircraft systems:UAVs design，development and deployment ［M］. UK: John Wiley ＆Sons，2010.

［4］申振晴，张斌，龚昂，等.无人机着舰引导信息处理方法研究［J］.电光与控制，2012，11(19):13-16.

［5］Smith S M，Dun S E，Hopkins T L，et al.Application of a modular AUV to coastal oceanography:case study on the explorer［C］//Proceedings of Oceans Conference，1995:1423-1432.

［6］Xiang X B，Jouvencel B，Parodi O. Coordinated formation control of multiple autonomous underwater vehicles for pipeline inspection［J］. International Journal of Advanced Robotic Systems，2010，7(1):75-84.

［7］Stevenson I，Nicholson P，Attieh A，etc.Ultra-high resolution seabed mapping using an AUV［J］. Sea Technology，2002，43(8):40-45.

［8］Wu Z，Wu X.Robust synchronized motion of parent -child autonomous underwater vehicles［C］//Proceeding of the 32ndChinese Control Conference，2013:5693-5698.

［9］吴泽伟，吴晓锋.基于有限时间系统同步的自治水下航行器回收控制［J］. 自动化学报，2013，39(12): 2164-2169.

［10］胡红波，宋涛.UUV 在水下态势感知中的应用［J］.水雷战与舰船防护，2013，21(4):57-61.

［11］李德远，吴汪洋，李晓晨.军用UUV 的发展与应用前景展望［J］.舰船电子工程，2012，32(4):22-35.

［12］梁迎久.一类切换非线性系统的全局有限时间镇定［J］.重庆工商大学学报:自然科学版，2014，31(1):8-13.

［13］Wu G，Zou J，Wan L，Sun H. Design of the basic motion control system for water-jet-propelled unmanned surface vehicle［J］.Control Theory ＆ Application，2010，27(2):257-262.

［14］廖煜雷，庄佳园，李晔，等.欠驱动无人艇轨迹跟踪的滑模控制方法［J］.应用科学学报，2011，29(4):428-434.

［15］廖煜雷.无人艇的非线性运动控制方法研究［D］.哈尔滨:哈尔滨工程大学，2012.

［16］林茜.状态误差反馈控制的主-从混沌系统同步研究［D］.武汉:海军工程大学，2011.

［17］杨涛，邵惠鹤.基于遗传算法混沌系统同步的研究［J］.控制理论与应用，2002，19(5):789-792.

［18］任子武，熊蓉，储健.基于混合类电磁机制算法的混沌系统控制与同步［J］.控制理论与应用，2011，28(7):1009-1014.

［19］Wang H，Han Z Z，Xie Q Y，et al.Finite-time chaos control via nonsingular terminal sliding mode control［J］.Communications in Nonlinear Science and Numerical Simulation，2009，14(6):2728-2733.

［20］Aghababa M P. Khanmohammadiv S，Alizadeh G. Finitetime synchronization of two different chaotic systems with unknown parameters via sliding mode technique［J］.Appllied Mathematical Modelling，2011，35(6):2080-3091.

［21］Wang H，Han Z Z，Xie Q Y，et al.Finite-time synchronization of uncertain unified chaotic systems based on the CLF［J］.Nonlinear Analysis:Real World Applications，2009，10(5):2842-2849.

［22］Li S H，Tian Y P. Finite-time synchronization of chaotic systems［J］.Chaos，Solitons ＆ Fractals，2003，15(2):303-310.

［23］刘云峰，杨小冈，缪栋.基于模糊滑模的有限时间混沌同步实现［J］.物理学报.2007，56(11):6250-6257.

［24］陈云.有限时间同步及其军事应用研究［R］.武汉:海军工程大学，2014.

［25］Bhat S P，Bernstein D S.Finite time stability of continuous autonomous systems［J］.SIAM Journal on Control and Optimization，2000，38(3):751-766.

［26］Yu S，Yu X，Shirinzadeh B，et al. Continuous finite-time control for robotic manipulators with terminal sliding mode［J］.Automatica，2005，41(11):1957-1964.

［27］吴晓锋.主-从Lur’e 系统混沌滞后同步研究［D］.广州:中山大学，2004.