基于改进量子粒子群优化算法的多UCAV 协同任务分配研究

赵雪森，王社伟，邵 校

(空军航空大学飞行器控制系，长春 130022)

多UCAV 任务分配是近年来UAV 领域研究的热点问题。多UCAV 协同任务分配目的是在满足资源、平台以及时间等约束条件下，将合适的任务在合适的时间分配给合适的UCAV，并使多UCAV 系统的整体任务效能达到最优［1］。它是一个约束条件众多而复杂的优化问题，其解空间随着目标总数的增加而增加，使其成为一个多参数、多约束的NP 问题。传统的数学方法求解十分困难，而智能算法提供了解决问题的新途径。量子粒子群算法［2］是智能优化算法中的一种，本文提出的改进型量子粒子群算法在量子粒子群算法的基础上加入了混沌机制和变异算子，提高了算法的寻优能力，有效避免算法陷入局部最优和过早的收敛。

1 多UCAV 任务分配MOIP 模型

1.1 任务分配问题描述

本文假设UCAV 在一个二维空间内执行任务，战场地形以及战场中的目标位置信息已预先获知。战场中有m 架UCAV，V={V1，V2，…，Vm}，t 个作战目标，T ={ T1，T2，…，Tt}，任务类型Mt={Classify，Attack，Verify}，分别代表侦察、攻击和毁伤评估任务，但不是每个作战目标都全部包含这3种任务类型，任务总数要求每架无人机至少执行一个任务，至多执行Tmax个任务，且每个任务被一架无人机执行。考虑无人机的能力约束和多无人机间的时间约束，使最终分配达到收益最大，损耗最小。

1.2 任务分配模型

首先定义二进制决策变量xi，j∈{0，1}，xi，j=1 时表示Vi执行任务Ti，xi，j=0 时无人机不执行任务。本文针对无人机在执行任务时的任务总飞行航程、任务完成时间、目标价值收益3 个重要指标进行分析。

1)任务总飞行航程J1。在实际作战中，UCAV 执行任务的路程越长，执行任务的时间就越长，所消耗的燃油也越多，被敌方所击落的概率也就越大，因此为了降低UCAV 所受的风险要缩短UCAV 编队执行任务的总航程。

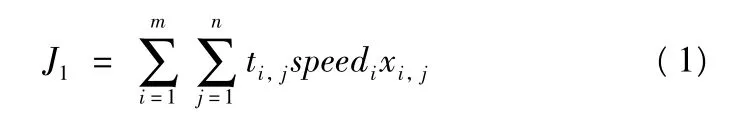
式(1)中，ti，j表示无人机Vi执行任务Tj的时间，speedi表示无人机的速度。

2)最长任务完成时间J2。战场环境瞬息万变，暴露在目标区域时间越长，无人机所受威胁越大。缩短完成任务时间最长的UCAV 的执行时间能够有效减低UCAV 被敌方防空武器击毁的概率。

3)目标价值收益J3。不同的任务相应具有不同的收益价值，在协同作战中，UCAV 应该尽可能地攻击高价值的目标，追求效益的最大化。

综合考虑上述3 个指标，多UCAV 协同任务分配模型定义为式(4)，为了求得指标函数最小，J3取为-J3。

1.3 任务分配约束条件

多UCAV 协同控制任务分配问题是一类约束条件众多的组合优化问题［3-4］，由于约束条件的耦合程度高，使得求解极为复杂，为了方便建模和算法的求解，下面从多机协同约束、任务时间约束、无人机任务类型及能力约束3 个方面进行考虑，给出协同控制约束条件的数学描述。

1.3.1 多机协同约束

每个任务只能被执行一次。

每架UCAV 一次只能执行一项任务。

每个目标包含的任务都要被执行。

1.3.2 任务时间约束

时间窗约束，给定时间窗口(aj，bj)，无人机Vi到达目标Tj时刻为tij。

1.3.3 无人机任务类型及能力约束

无人机任务类型约束，Mti，j为UCAV Vi执行的任务Mj的任务类型，MKind(Vi)为Vi所能执行的任务类型。

无人机能力约束，Di为UCAV Vi的最大航程。

2 改进的量子粒子群优化算法

2.1 量子粒子群优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)是在1995年由美国社会心理学家Kennedy 和电气工程师Eberhart提出的［5-6］，主要思想来源于对鸟类群体行为的研究。自提出以来，由于其计算简单、收敛速度快、易于实现、控制参数少等特点，引起了国内外相关领域众多学者的关注和研究，越来越多的被应用于优化问题中。但PSO 算法在优化过程中易出现早熟现象，不能保证收敛于到全局最优解，甚至于局部最优解。目前已提出了多种PSO 改进算法，如变异粒子群算法、自适应调整粒子群算法、免疫粒子群算法［7］，这些算法在一定程度上可避免PSO 陷入局部最优，但对算法易懂性、可操作性考虑太少，并且增加了算法的计算量。

为了更好地解决上述问题，sun 等［8-9］在研究了Clerc等人的关于粒子收敛行为的研究成果后，从量子力学的角度出发，提出了一种新的PSO 进化模型，这种模型以DELTA 势阱为基础，认为粒子具有量子行为，在模型的基础上提出了量子粒子群优化算法。该算法对整个PSO 算法的进化搜索策略进行了修改，进化方程中不再需要速度向量，而且整个迭代方程参数更少，更容易控制。在量子空间中粒子满足聚集态的性质完全不同，它可以在整个可行解空间中进行搜索，因而QPSO 算法的全局搜索性能远远优于标准PSO算法［10］。

QPSO 算法利用波函数φ(x，t)来描述粒子的状态，并通过求解薛定谔方程得到粒子在空间某一点出现的概率密度函数，再通过Monte Carlo 随机模拟得到粒子的位置方程为

式(11)中:u 是在［0，1］上服从均匀分布的随机数;L 值由式确定，

则QPSO 算法的进化方程为

式(14)中:φ 和u 是［0，1］上均匀分布的随机数，α 为收缩扩张系数，M 为种群中粒子的数目，N 为粒子的维数，Pi，j(t)和Gj(t)分别是粒子所经历的最好位置和种群中所有粒子所经历的最好位置。

2.2 混沌思想

混沌是一种貌似无规则的运动［11-13］，指在确定性非线性系统中不需要附加任何随机因素即可以类似随机的行为，随机性使得搜索能够避免陷入局部最优。混沌系统另一个最重要的特性就是遍历性，它通过迭代产生的解能够覆盖目标区域内所有的点，只要控制得当，最终解可以以任意精度逼近真实的最优解。由于混沌系统的随机性、遍历性等特点，可以将混沌与量子粒子群算法相结合，来提高算法的性能。Logistic 映射是一种经典的混度映射，非常简单且被广泛应用，定义如下:

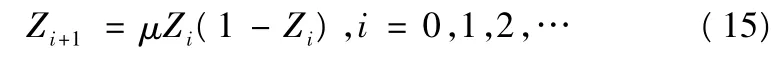
其中，μ∈(2，4］，当μ=4 且Z0∈(0，1)时方程处于完全混沌状态。首先将决策变量xi，j按式(16)映射为［0，1］之间的混沌变量:

因为Logistic 映射在［0，1］上完全遍历，所以将混沌系统应用到算法中，可以改善早熟收敛的问题。本文中采用采用混沌系统来初始化粒子的位置，这样既不改变算法初始化时的随机性，又可以利用混沌特性来提高种群的多样性和搜索的遍历性［12］。

2.3 高斯分布变异算子

混沌思想是在粒子初始化时增加群体的多样性，而变异操作是在寻优过程中增加群体多样性的有效手段。高斯概率分布是一类应用最广泛的连续概率分布形式，当种群陷入局部最优时，通过增加一个扰动来解决这个问题。

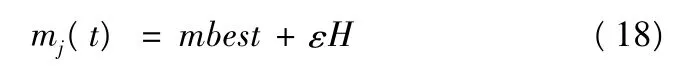
其中ε 是预先规定的参数，本文设为ε=0.001，H 是满足均值为0 方差为1 的高斯随机分布。则式(14)变为

满足高斯概率密度分布的变化方式具有很强的局部搜索能力，有利于提高算法的局部搜索精度。本文设置粒子群的变异作用随着代数的迭加而降低，即在寻优初期作用于所有粒子，在寻优中期作用于部分粒子，而在寻优后期则不再变异，使粒子能够在最优解邻近区域进行精细搜索。高斯变异算子作用方式如图1 所示。改进的量子粒子群算法(IQPSO)的流程如图2 所示。

图1 高斯变异算子作用方式示意图

图2 改进的QPSO 算法的流程

3 多UCAV 协同任务分配仿真

3.1 粒子编码方式

多无人机任务计划中的任务分配情况和执行次序都是自然数，因此需要对粒子的位置进行整数化处理。在粒子初始化和更新过程中，若某一维出现非整数，则按照四舍五入原则取整。编码采用双层整数编码方式，第1 行表示执行任务的UCAVi，第2 行表示与第1 行UCAV 序列所对应的执行目标序列，如图3 所示。

图3 双层编码示意图

图中目标出现的次序表示对应UCAV 执行的任务类型，第1 次出现代表执行的为侦察任务，第2 次代表攻击任务，第3 次代表评估任务。

3.2 适应度函数的建立

上述编码方式可以满足部分约束条件，但在任务超出无人机最大航程和不满足时间窗约束时则需要对适应度函数加一个惩罚项将约束问题转化为无约束问题。

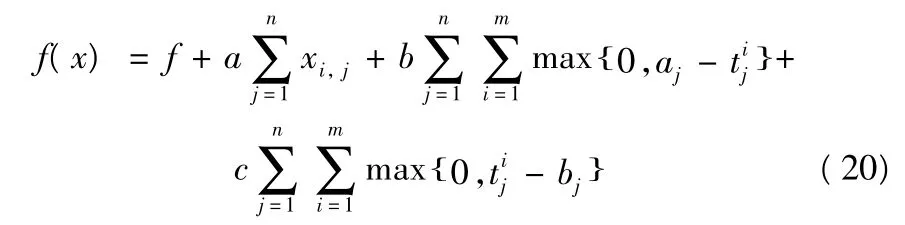
式(20)中，系数a，b，c 用于对不同类型的惩罚进行一个尺度变换。

3.3 仿真示例

为验证算法的有效性，针对3 架无人机对5 个敌方目标的任务进行仿真实验，需要对目标进行侦查、攻击以及评估3类任务，共计15 个待执行任务，分别用C、A、V 进行表示。UCAV 和敌方目标的位置如图2 所示，具体数据如表1 ～表3所示，在不影响任务分配算法验证的前提下简化仿真实验过程，假设飞行航路为直线，且所有待执行任务很短时间内即可完成。位置坐标均为km，无人机巡航速度360 km/h，最大航程3 500 km，任务价值经归一化处理，每个算法运行30 次取最好值，最大迭代次数600，粒子数为50，PSO 算法中c1=c2=2，α 与β 范围从0.9 到0.2 线性递减。实验初始设置图如图4 所示。

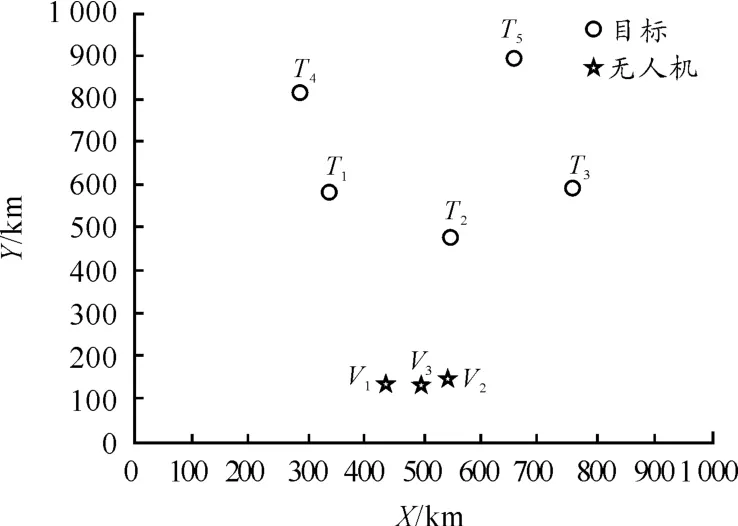
图4 仿真实验初始设置图

3.4 仿真结果及分析

仿真的结果如下所示，表4 为3 种算法任务分配的结果，表5 为3 种算法在执行时间、整体代价和价值收益上的对比，图5 为任务航程代价随迭次数变化的曲线图。

表1 无人机性能参数

表2 目标任务信息表

表3 任务时间窗约束

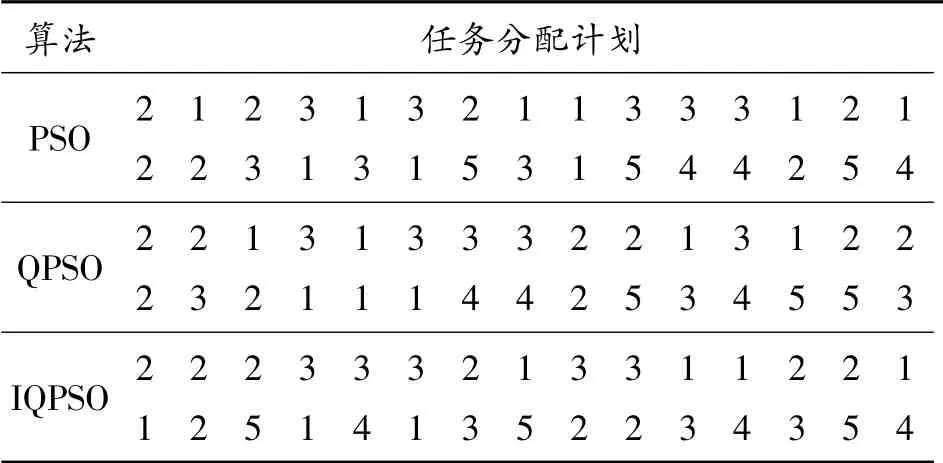
表4 PSO、QPSO、IQPSO 算法分配结果

表5 PSO、QPSO、IQPSO 算法所得结果比较

图5 总任务航程代价曲线

通过图表可以看出3 种算法均能完成预定任务的分配，每个目标都可以完成，但在任务的整体代价和执行时间上改进算法则明显低于其余两种算法，从图5 中看出改进算法的收敛速度提高。通过仿真结果表明改进的算法在迭代过程中能够帮助粒子跳出局部最优值，有效完成任务，验证了算法的有效性。

4 结论

本文以为任务总飞行航程最小、任务完成时间最短、目标价值收益最大为目标构建了多UCAV 协同任务分配模型，在QPSO 算法的基础上采用混沌机制和变异因子来提高种群的多样性，改进的QPSO 算法能够在保持快速性的同时有效的跳出局部最优解，克服了QPSO 易陷入局部最优的不足。最后仿真结果验证该算法优于QPSO 算法，能够有效的解决多UCAV 协同任务分配问题。

［1］Bryson M，Sukkarieh S.Decentralised Trajectory Control for Multi-UAV SLAM［C］//Proceeding of the 4th International Symposium on Mechatronics and it’sApplications.Sharjah，Uited Arab Emirates:IEEE，2007:1-6.

［2］宁涛. 混合量子算法在车辆路径问题中应用的研究［D］.大连:大连海事大学，2013.

［3］霍霄华，陈岩，朱华勇，等.多UCAV 协同控制中的任务分配模型及算法［J］.国防科技大学学报，2006，28(3):83-88.

［4］龙国庆，祝小平，周洲.多无人机系统协同多任务分配模型与仿真［J］.飞行力学，2011，29(4):68-76.

［5］Kennedy J，Eberhart R.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks，1995:1942-1948.

［6］Eberhart R，Kennedy J. A new optimizer using particle swarm theory［C］//Proceeding of the 6th International Symposium on Micro Machine and Human Science.Nagoya，Japan:IEEE Service Center，1995:39-43.

［7］高海昌，冯博琴，朱利.智能优化算法求解TSP 问题［J］.控制与决策，2006，21(3):241-247.

［8］Sun Jun，Feng Bin，XuWenbo. Particle swarm optimization with particles having quantum behavior［C］//Proceedings of The IEEE Congress on Evolutionary Computation(CEC).USA，IEEE Presss，2004:325-331.

［9］Sun Jun，XuWenbo，Feng Bin. A global search strategy of quantum-beaved particle swarm optimization［C］//2004 IEEE Conference on Cybernetics and Intelligent Systems.USA，IEEEE Press，2004:111-116.

［10］李川.基于混合量子进化算法的随机车辆路径问题的研究［D］.浙江工业大学，2011.

［11］高尚，杨静宇.群智能算法及其应用［M］.北京:中国水利水电出版社，2006.

［12］Chang Junlin，An Fengshuan，Su Pizhao. A quantum-PSO algorithm for no-wait flow shop scheeduing problem［C］//2010 Chinese Control and Decision Conference. Xuzhou，China:IEEE Press，2010:179-184.