不同浪向下船舶动力定位的动力学分析
张大朋,朱克强,严心宽,姬芬芬
(宁波大学海运学院,宁波315211)
不同浪向下船舶动力定位的动力学分析
张大朋,朱克强,严心宽,姬芬芬
(宁波大学海运学院,宁波315211)
参考某动力定位船舶的具体参数和该船的海浪响应幅值算子(RAO),结合该船工作时的具体过程,利用大型水动力分析软件OrcaFlex建立了船舶动力定位时的动力学分析简化模型。通过调节不同海况下的浪向,实现了对动力定位船舶在不同浪向下的动力学分析,对海浪作用下船舶的纵荡、横荡和转艏运动进行了数值仿真,得到了不同浪向对船舶动力定位精度的影响,确定了船舶动力定位时的最佳浪向,结合计算结果,给出了船舶动力定位的优化设计方案。
动力定位;OrcaFlex;动力学分析;不同浪向
随着海洋开发不断向远海深海扩展,传统的多点锚泊系统己经不能满足深海地区船舶定位的作业要求[1]。其缺点是:定位精度不够,其准确性与水深成反比;机动性能差,一旦抛锚,当需要重新定位时,需要重新定位抛锚过程繁琐;应用受到水深及海况的限制。为了满足更高的作业施工要求,动力定位系统(Dynam⁃ic Positioning System)应运而生。
动力定位系统是指海上漂浮物依靠自身的动力[2],如主推进器、舵、侧推等在控制系统的指挥下抵抗外界干扰,使自身保持某一姿态和舷向,悬停在空间的某一定点位置或沿着某一轨迹航行,它具有不受海水深度影响、定位准确快速等优点。
自由船舶或者海洋平台漂浮在海上时,要受到来自风、海流和波浪等环境因素所产生的力和力矩的作用,致使船舶或平台产生平移和舷向的改变,并会发生横摇、转艏运动[3],如果这些船舶或平台需要定位在海面上的某一个固定的位置,那么船舶就必须能够依靠自身的动力相应地产生反力与反力矩来抵抗这些变化,使船舶保持在以大地坐标系为参考的某一个固定的位置上,并且保持一定的指向,即定点控制;或者使船舶在作业的过程中,以特定的速度,沿着一条事先给出的大地坐标系下的轨迹航行,并且保持船舶的指向以满足作业的要求,直到终点,即循迹控制。
海上动力定位船舶受到风、浪、流等干扰力的作用,其中缓慢变化的流力、风力以及二阶浪力使船产生低频运动,一阶浪力使船产生高频运动。海浪干扰对动力定位船舶的运动影响很大,随机性较强,因此船舶对海浪的响应相当复杂。而浪向的改变会对船舶的动力定位产生不同的影响,甚至会威胁到施工作业的安全。本文以大型水动力分析软件OrcaFlex软件为平台,建立了不同浪向作用下船舶动力定位时的动力学分析模型,并对其进行模拟仿真,通过时域耦合动力分析方法分析船舶动力定位系统的非线性动力学特性。为了最大限度的确保模拟的真实性,模拟的时间步长不应超过模型最短自然周期的1/10。结合水动力性能的计算结果给出了一些指导性的建议,对于保证海上安全作业有重要意义。
1 海洋环境载荷的计算理论
1.1波浪理论的选择
研究船舶在随机海浪作用下的运动特性和船舶动力定位系统在海浪作用下的动态响应时,经常把海浪作为一个平稳随机过程来处理[4]。波浪冲击过程比较复杂[5],现实中的波浪为由多个振幅不同、频率不同、相位差不同的单元波叠加而成,为尽量确保波浪的真实性,利用谱分析来研究具有平稳随机过程的波浪的统计特性。利用“北海联合海浪计划”(JONSWAP)谱对海浪进行设定。该谱的优点之一在于引进峰升高因子γ来描述风浪的成长状态[6]。JONSWAP谱公式为

式中:a为无因次常数;通过指定有效波高Hs和波浪周期Tz得出;f为波浪频率;fm为波峰频率;g为万有引力常数;γ为谱峰提升因子,取平均值。

1.2船体RAO
RAO,即response amplitude operator,可以用来计算船舶在海中工作时的行为。船体RAO一般可以通过船舶的水池模型实验来获得。本质是一个由波浪激励到船体运动的传递函数,在OrcaFlex中,一旦船体的RAO确定,那么波浪所引起船体的运动就将是确定的[7]。
船体运动响应特性可以用船体响应幅频因子(RAO)进行描述。一阶波浪力所引起的船体偏移用响应幅频因子(RAO)进行定义,如下

式中:x为浮体位移响应(升沉、纵荡、横荡是长度单位,艏摇、横摇、纵摇是角度单位);a,ω为波浪的振幅和频率;R为RAO响应的系数;φ为相位;RAO的坐标原点取在船体的设计水线处。
1.3动力定位施加反力及反力矩的计算
推力器系统主要是对安装在船体的各个推力器(一般不少于5个)进行推力分配,并且借助它们得到相应的推力和力矩,以抵抗作用于船的干扰力和力矩。而在OrcaFlex中,在建好模型后,系统会根据不同的外部环境参数自动地给船体的各个推进器通过乘以不同的反力系数Kf、反力矩系数Km进行最优分配,以达到使船体在允许误差范围内定位的目的。
2 在OrcaFlex中船舶动力定位动力学模型的建立
2.1坐标系、风浪流方向的确定OrcaFlex用一个全局坐标系G-XYZ来确定坐标轴,其中G代表全局坐标系的起点,GX、GY、GZ分别表示X轴、Y轴及Z轴。对于不同的物块模型,也有相对应的局部坐标系。风浪流相对于x轴和y轴的方向是相对全局坐标系中的GX轴和GY轴而言的,具体如图1、图2所示。
2.2OrcaFlex中船体主尺度的确定
根据实际船体主尺度在OrcaFlex软件中建的模型中船长为103 m,型宽为16 m,型深为13.32 m。设计吃水为6.66 m,横稳性半径1.84 m,纵稳性半径114 m,排水量8 800 t,水面上正面投影191 m2,水面上侧面投影927 m2。方形系数CB为0.804,首摇转动惯性矩为5.83×109kg·m2。本船的RAO、波浪漂移QTFs、附加质量系数及阻尼系数的数据均来自一个103 m长的实船在400 m水深水池的NMIWave衍射分析。

图1全局及局部坐标系示意图Fig.1Global and local coordinate system
图2风浪流方向示意图Fig.2The direction and headings
2.3OrcaFlex中模型的建立
模型建成后(图3),在本模型中,有3艘船,左侧船为动力定位的理想目标位置,右侧船为加装了动力定位系统的船舶,上方船舶为没有加装动力定位系统的船舶,在本模型中主要是与加装了动力定位系统的船舶做对比。

图3动力定位模型示意图Fig.3Schematic model of dynamic positioning system
3 计算结果
设计中主要考虑如下特征海况条件作为设计边界条件:水深为100 m,浪向取为0°~180°;波高为7 m,周期为8 s。
目标的定位位置为:在全局坐标系下,船体横向坐标X为30 m,纵向坐标Y为-20 m,转艏角为90°。
3.1无动力定位系统船舶的横荡、纵荡、转艏的变化情况

图4无动力定位系统横荡历时的仿真结果Fig.4The sway versus time curve

图5无动力定位系统纵荡历时的仿真结果Fig.5 The surge versus time curve

图6无动力定位系统艏摇历时的仿真结果Fig.6 The yaw versus time curve
图4~图6为无动力定位系统的船舶随浪向改变时船舶的横荡、纵荡和转艏变化情况。对比图4、图7,图5、图8发现,无动力定位系统时船舶的横荡和纵荡幅度很大,在船体随波逐流的过程中,横荡和纵荡幅度甚至达到了上千米。图4显示,随着浪向的改变,船体的横荡方向会发生改变,当浪向在1°~90°时,船体往船舶右舷方向横荡,且随着浪向角的增大横荡幅度依次减小;当浪向角为90°~180°时,船体往船舶左舷方向横荡,且随着浪向角的增大横荡幅度依次增大。
图5显示,随着浪向的改变,船体的纵荡幅度会发生改变,当浪向在1°~90°时,船体往船艏方向纵荡,且随着浪向角的增大横纵荡幅度增大,当浪向角达到90°时,纵荡幅度达到最大;当浪向角在90°~180°时,船体仍旧往船艏方向纵荡,且随着浪向角的增大纵荡幅度依次减小,当浪向角达到180°时纵荡幅度达到最小。而产生上述2种现象的原因是,浪向的改变使得船体相对浪向的面积发生了改变,进而导致了作用在船体横荡和纵荡方向的波浪力发生了变化,而且这种模拟计算结果也和理论计算结果相一致。对比图6、图9发现(无动力控制时船体的转艏角度很大),当无推进器控制时,除浪向为180°外,其他浪向时,船体总体上往右舷转动,且转动幅度是有动力定位系统船舶的十几倍。
3.2动力定位船舶的横荡、纵荡、转艏的变化情况
观察图7~图9发现,动力定位船舶在不同浪向下的横荡、纵荡和艏摇的历时图像均呈周期性往复变化,这种周期性往复循环式变化在横荡和艏摇历时图像表现得尤为明显。对比图7和图8发现,图8的图像相对于图7而言较为紧密,这说明,对于动力定位船舶而言,相对于船体的纵荡,浪向的改变对船体横荡的影响程度更大,而纵荡与横摇的自振周期亦不相同。图9说明,动力定位船舶的艏摇比较微弱。
在此说明一点,图中的坐标均是动能定位船舶在进行仿真时的大地坐标系,因此船体某一时刻的坐标要加上目标的定位位置的坐标值。
3.3动力定位船舶施加的反力、反力矩的变化情况
对比观察图10、图11发现,浪向的改变对推进器纵荡方向的约束反力影响程度更大,也就是说,随着浪向的改变约束纵荡方向的反力变化要比约束横荡方向的反力变化明显。结合对比图7、图8,不难解释这一现象:正是因为图10和图11中推进器对船体纵荡方向约束反力变化比横荡方向的剧烈,从而使得随着浪向的改变,对船体纵荡方向的约束大于对船体横荡方向的约束,这也正是图8的图像相对于图7而言较为紧密的原因。观察图12发现,推进器的总约束反力随着浪向的改变而改变,当浪向为90°~180°时推进器的总约束反力要大于1°~90°时推进器的总反力,且当浪向在90°~180°时,推进器的总反力随着浪向角的增加而递增;产生这种现象的原因为,推进器的纵荡约束反力相对于横荡约束反力对浪向的改变更加敏感,而当浪向变为90°~180°时,随着浪向角的改变使得纵荡约束反力相对于浪向角为1°~90°时发生了巨大的变化,但随着浪向的改变横荡约束反力变化不大,这也就导致了二者的合力-推进器总约束反力在浪向角为90°~180°发生了上述变化。对比观察图9、图13发现,二者的曲线在外型上呈现很大的相似性,且都表现出一定的周期性,这说明转艏角的变化直接影响推进器艏摇约束反力矩的大小。
4 结论
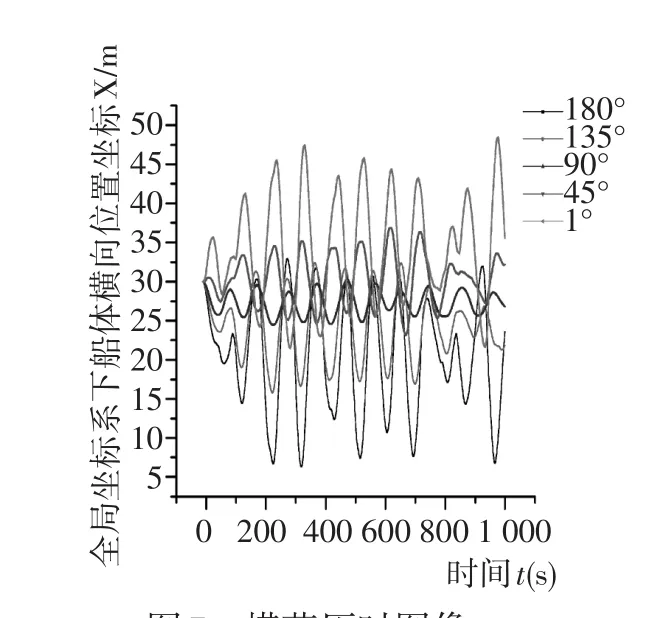
图7横荡历时图像Fig.7The sway versus time curve

图8纵荡历时图像Fig.8The surge versus time curve

图9艏摇历时图像Fig.9The yaw versus time curve

图10推进器横荡方向反力历时图像Fig.10The applied Lx-Force versus time curve

图11推进器纵荡方向反力历时图像Fig.11The applied Ly-Force versus time curve
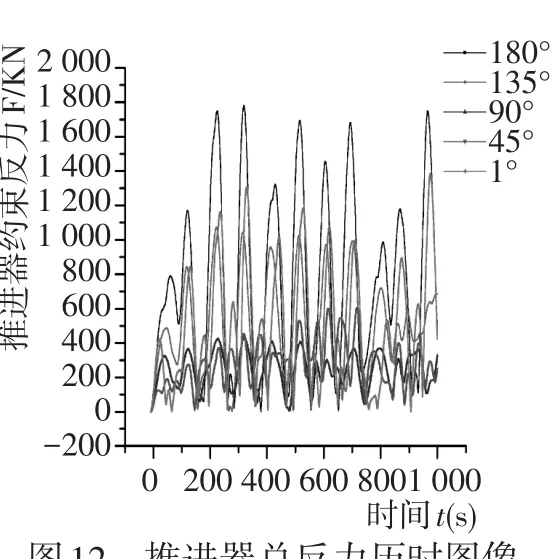
图12推进器总反力历时图像Fig.12The applied Force versus time curve

图13推进器艏摇反力矩历时图像Fig.13The applied Lz-Moment versus time curve
(1)动力定位船舶在不同浪向下的横荡、纵荡和艏摇的历时图像均呈周期性往复变化,这种周期性往复循环式变化在横荡和艏摇历时图像表现的尤为明显。对于动力定位船舶而言,相对于船体的纵荡,浪向的改变对船体横荡的影响程度更大。(2)浪向的改变对推进器纵荡方向的反力影响程度更大,也就是说,随着浪向的改变推进器纵荡方向的反力变化情况要比横荡方向的反力变化明显。这对于在设计船舶的动力定位系统有很重要的指导意义,可根据实际工况的需要对动力定位系统的各个推进器的布局及结构进行优化设计,以达到最佳工作效果。(3)无动力定位系统时船舶的横荡和纵荡幅度很大,在船体随波逐流的过程中,横荡和纵荡幅度甚至达到了上千米。(4)对于无动力定位系统的船舶而言,随着浪向的改变,船体的横荡方向会发生改变,当浪向在0°~90°时,船体往船舶右舷方向横荡,且随着浪向角的增大横荡幅度依次减小;当浪向角在90°~180°时,船体往船舶左舷方向横荡,且随着浪向角的增大横荡幅度依次增大。(5)对于无动力定位系统的船舶而言,随着浪向的改变,船体的纵荡幅度会发生改变,当浪向在0°~90°时,船体往船艏方向纵荡,且随着浪向角的增大横纵荡幅度增大,当浪向角达到90°时,纵荡幅度达到最大;当浪向角90°~180°在时,船体仍旧往船艏方向纵荡,且随着浪向角的增大纵荡幅度依次减小,当浪向角达到180°时纵荡幅度达到最小。(6)由于OrcaFlex软件本身的限制,本仿真在一定程度上来说还是比较粗糙的,但还是能说明及解决一些在实际工作中的问题。下一步将着手运用matlab中的simulink对动力定位系统进行更加精确地仿真。
[1]吴楠,陈红卫.船舶动力定位仿真系统设计[J].舰船科学技术,2013,35(5):103-110. WU N,CHEN H W.Simulation design on dynamic positioning system of vessels[J].Ship Science and Technology,2013,35(5): 103-110.
[2]童进军,何黎明,田作华.船舶动力定位系统的数学模型[J].舰船工程,2002(5):27-29. TONG J J,HE L M,TIAN Z H.Mathematical model of dynamically positioning system of ship[J].Ship Engineering,2002(5):27-29.
[3]刘喜传.海洋石油286船三级动力定位系统设计[J].舰船设计通讯,2012,1(130):52-55. LIU X C.Introduction of 3 class dynamic positioning system design for HAIYANGSHIYOU 286[J].Journal of Ship design,2012,1(130):52-55.
[4]王立军,陈锋,丁福光,等.船舶动力定位海浪环境的实时仿真与海浪谱分析[J].华东船舶工业学院学报,2001,15(1):48-51. WANG L J,CHEN F,DING F G,et al.Real⁃time simulation and spectrum⁃analysis of a dynamic positioning system ship in waves[J].Journal of East China Shipbuilding Institute,2001,15(1):48-51.
[5]郭保臣,任冰,刘明.波浪冲击作用下海洋结构物的动力响应[J].水道港口,2011,32(3):168-172. GUO B C,REN B,LIU M.Dynamic responses of marine structures due to wave impact[J].Journal of Waterway and Harbor,2011, 32(3):168-172.
[6]郭佩芳.JONSWAP谱的几个参量的研究[J].海洋与湖沼,1992,23(4):350-354.
Dynamic analysis of dynamic positioning system of vessel under different wave directions
ZHANG Da⁃peng,ZHU Ke⁃qiang,YAN Xin⁃kuan,JI Fen⁃fen
(Faculty of Maritime and Transportation,Ningbo University,Ningbo 315211,China)
Based on the parameters of a certain vessel with dynamic positioning system and the response ampli⁃tude operator(RAO),combined with the specific process of the vessel at work,the model of the vessel with dynamic positioning system was established by using OrcaFlex.With the change of the direction of wave,the dynamic analy⁃sis of the system was made under different wave directions.At the same time,the digital simulation of ship′s surge, sway and yaw motions were made.And the extent of influence on the dynamic positioning system under different wave directions and the optimum wave direction for the operation of dynamic positioning were gotten.According to the calculated result,the optimization design of the operation of dynamic positioning for the vessel was given.
dynamic positioning system;OrcaFlex;dynamic analysis;different wave directions
TV 131.2;U661
A
1005-8443(2015)04-0313-05
2015-04-08;
2015-05-28
长江学者和创新团队发展计划资助项目(IRT0734);国家自然科学基金资助项目(11272160);浙江省自然科学基金资助项目(LY13A020006);国家高技术研究发展计划(863计划)(2014AA09A224)
张大朋(1987-),男,山东省聊城人,助理研究员,主要从事船舶与海洋工程结构物动态响应方面研究。
Biography:ZHANG Da⁃peng(1987-),male,assistant professor.

