SWAN与CGWAVE嵌套模型在设计波要素计算中的联合应用

王少朋，李瑞杰,2，吉鸣，董啸天，朱文瑾

（1.河海大学海岸灾害及防护教育部重点实验室，南京210098；2.河海大学环境海洋实验室，南京210098；3.浙江省舟山市交通规划设计院，舟山316021；4.淮海工学院土木工程学院，连云港222006）

SWAN与CGWAVE嵌套模型在设计波要素计算中的联合应用

王少朋1，李瑞杰1,2，吉鸣3，董啸天1，朱文瑾4

（1.河海大学海岸灾害及防护教育部重点实验室，南京210098；2.河海大学环境海洋实验室，南京210098；3.浙江省舟山市交通规划设计院，舟山316021；4.淮海工学院土木工程学院，连云港222006）

以舟山东福山岛码头为例，利用SWAN与CGWAVE建立的大、小范围波浪嵌套模型对码头附近海域进行波浪计算，经验证表明大范围计算结果准确性较好，从中提取-50 m等深线处波要素作为小范围边界条件，利用CGWAVE模型对码头附近海区进行小范围波浪计算，并提取码头前沿波要素并进行分析。研究结果表明SWAN与CGWAVE模型的联合应用在东福山岛码头设计波浪计算中具有良好的适应性，为港口工程的设计、建设提供了科学依据和理论借鉴。

SWAN模型；CGWAVE模型；联合应用；设计波要素

波浪是海岸工程中非常重要的因素，外海深水区的波浪传播到近岸浅水区时，受到海底地形变化、底摩擦和障碍物等各种因素的影响，发生折射、绕射、反射和破碎等一系列变形［1］。准确计算设计波浪分布，是海岸工程设计规划的前提条件。近年来，常用数学模型主要有3种：（1）缓坡方程，计算软件有CGWAVE模块和TK⁃2D中的波浪模块等；（2）Boussinesq方程，MIKE 21中的BW模块等；（3）能量平衡方程计算软件有SWAN模块等［2］。

码头是海岸地区重要的工程建筑物，是船舶停靠、货物装卸的重要场所。波浪是影响近岸海域最重要的水动力因素，码头附近海域的波浪条件是码头规划建设中首要考虑的问题［3］。SWAN、CGWAVE模型分别在大尺度、小尺度的模拟精度较高，但SWAN模型在复杂地形下小尺度波浪传播计算的精度仍不及CG⁃WAVE模型，而CGWAVE模型一旦计算区域稍大，就会因为网格数过多而难以进行计算，两者很少被联合应用于实际工程的波浪计算。以舟山东福山岛码头为例，该海域海底地形复杂，波浪在由外海向近岸传播过程中会发生一系列变形现象，如果利用单一模型进行计算，则计算尺度和计算精度不能兼顾，研究利用大小网格嵌套的SWAN模型与CGWAVE模型相结合的方式对该海域进行波浪要素计算。

1 模型的建立

1.1SWAN模型介绍

SWAN模型［4］以二维动谱密度表示随机波，直角坐标下，动谱平衡方程其表达形式为

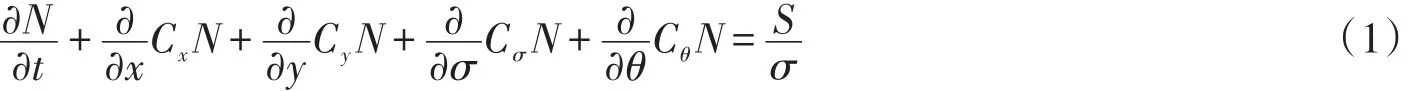
式中：左边第1项为N随时间的变化率；第2和第3项表示N在地理坐标空间x、y方向的传播；第4项为由于流场和水深引起的N在相对频率σ空间的变化；第5项为N在谱分布方向θ空间（谱方向分布范围）的传播；S为以谱密度表示的源汇项，包括风能输入、波与波之间非线性相互作用和由于底摩擦、白浪、破碎引起的能量损耗；Cx、Cy、Cσ、Cθ分别代表在x、y、σ和θ空间的波浪传播速度。

SWAN模型全面考虑波浪浅化、反射、折射、底摩擦、破碎、风能输入及波浪非线性效应，模型采用全隐式有限差分格式，无条件稳定。该模型已成功应用于海岸、河口及近海水域的波浪预报［5-7］。

1.2模型参数的选取及计算条件

大范围波浪数学模型计算区域如图1所示，共5条开边界，北面以长江口南支以南的北东海海域为北开边界，南面以石浦港及牛鼻山以南海域为南开边界，东面以东福山岛以东约75 km的东海海域为东开边界，西面以黄湾镇南杭州湾口为开边界，其他均为固边界。计算区域采用非结构三点式三角网格进行剖分，并在研究海域进行局部加密（图2），最小网格尺寸为19 m，节点数为37 150，网格数为71 156。

嵊山海洋观测站位于北纬30°42′，东经122°49′，与工程区大致处于同一经度，地形相似且都不受遮挡的直面外海，其波要素能代表工程区附近海域的波浪设计要素，该测波站的波浪资料对N向至S向等（顺时针）9个方向外海来向波浪有较好的代表性，因此采用这九个方向的海向波高资料作为大范围波浪数值模拟结果外海方向波浪的率定数据。收集该站1995～2012年这9个方向的最大波高及频率资料，并拟合此9个方向波高的P-Ⅲ曲线，获取各重现期波浪要素作为海向计算的外海起波边界；同时收集普陀山气象站的1994～2013年其他7个方向（陆向）的风速资料，并转化为海面上10 m高度处的风速值，该气象站与工程区域约44 km，为了保证风速资料的可用性，拟采用风浪成长公式推算出陆向7个方向的波高值及周期值作为大范围波浪数值模拟结果陆向波浪的率定数据。采用“莆田海堤试验站公式”推算设计波浪作为陆向计算的边界条件，为了节省篇幅，只考虑对该海域有较大影响的几个方向。计算水位采用50 a一遇高潮位,为2.0 m，以上构成了SWAN模型的计算条件（表1～表2)。

莆田海堤试验站公式

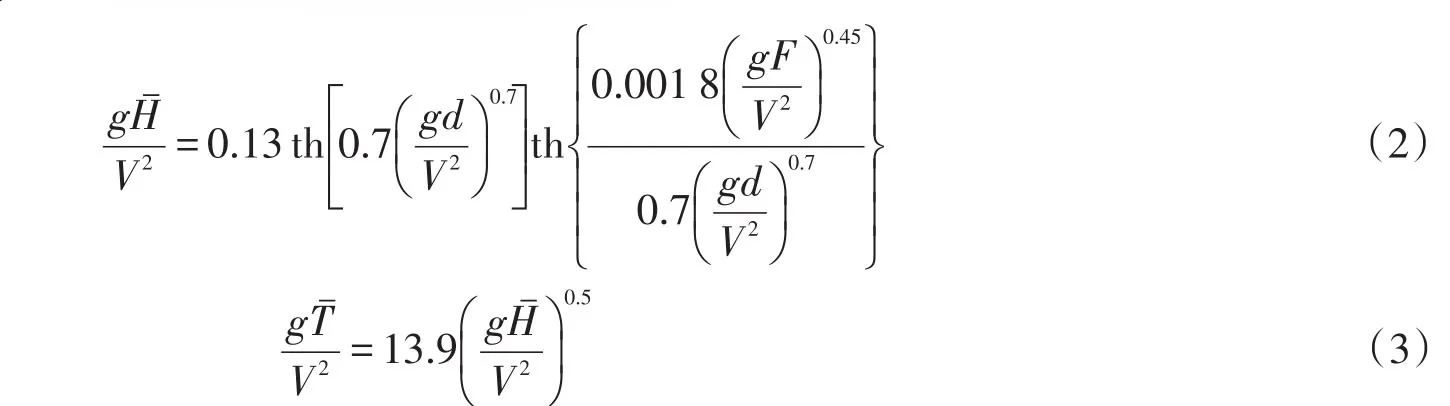
式中：g为重力加速度，9.81m s2；F为风区长度，m；V为设计风速，m s；d为水深即风区平均计算深度，m；Hˉ为平均波高，m；Tˉ为平均波周期，s。

大范围开边界波浪入射条件采用河海大学环境海洋实验室根据WAVEWATCH-III模型和SWAN模型开发的全球波浪数值模拟软件提供,小范围波浪数学模型的开边界波浪入射条件由大范围计算得到（图3）。

大范围波浪传播的计算结果表明，由于地形及岛屿阻挡作用，外海NW、NNW、N、NNE 4个方向来波在传至码头附近海域时，传播方向均发生不同程度的偏转：NW向波浪偏转为N向，NNW向及N向偏转为NNE向，NNE向偏转为NW向。

图1大范围计算区域Fig.1Large computational domain

图2计算区域网格示意图Fig.2Meshes of computational domain

表150 a一遇海向边界条件Tab.1Boundary conditions of oceanic direction under 50⁃year return period

表250 a一遇陆向边界条件Tab.2Boundary conditions of continental direction under 50⁃year return period

小范围波浪数学模型的开边界波浪入射条件是由大范围计算得到，大范围计算模型的准确性对小范围数学模型的计算结果有着重要影响，因而应对大范围模型进行验证。对嵊山海洋站波浪观测站提供的N向和NNE的波高资料进行数据整理和推算，将得到的波高值和周期值与大范围波浪数学模型的计算结果进行对比和验证（表3）。利用普陀气象站测得的NW向及NNW向的风速资料，根据风浪成长公式推算该海域的波浪要素并与大范围波浪数学模型的计算结果进行比较验证（表4）。由表3和表4可知，利用SWAN模型计算的有效波高模拟值与推算值差别很小，吻合度较高，偏差基本在3%之内；陆向波浪的周期值的模拟值相比推算值差别不大，海向方向的模拟值比推算值稍高，整体上差别不大。即建立的大范围波浪数学模型能够较好的反应浙北海域的波浪场分布情况，可为小范围波浪数学模型提供波浪入射边界。

1.3CGWACVE模型介绍

CGWAVE［8］模型是Berkhoff基于小振幅波和缓坡的假定，采用沿水深积分的方法得出联合折射、绕射的二维波浪变形方程——椭圆型缓坡方程。该方程结合固边界的反射边界条件，构成波浪传播变形的联合折射、绕射、反射数学模型。在上述缓坡方程的基础上，Dalrym⁃ple和Kirby［9］、Zhao和Panchang［10］、李瑞杰［11］等对方程进行了拓展，得到联合波浪折射、绕射、反射，考虑陡变地形、能量耗散以及非线性效应的缓坡方程如下

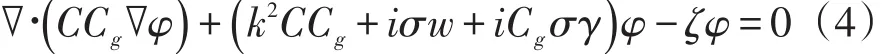
1.4模型参数的选取及计算条件

小范围网格采用非结构三点式三角形网格剖分计算区域，网格步长控制在一个波长内有12个网格节点，以满足波浪条件。由于码头附近地形变化较大，特别是工程区域沿N向水深变化较剧烈，如图5所示，东福山岛拟建交通码头前沿最小网格长度约1.5 m,各波向计算组合区域如图3所示。除入射边界外，其他海边界均为吸收边界，反射系数取为0.0，由于该海岸为基岩海岸，岸边界反射系数取0.3。

图3大范围波浪场分布图Fig.3Distribution of wave field at large computation domain

表3海向波要素推算值与模拟值对比Tab.3Comparison of calculated wave parameters and estimated ones on oceanic direction

表4东福山陆向入射波浪波要素验证Tab.4 Comparison of calculated wave parameters and estimated ones on continental direction

图4小范围计算网格示意图Fig.4Meshes of small computational domain

图5工程区域附近地形图Fig.5Topography of the area near engineering area

根据码头工程海域的地形分布特点，在各入射方向外海水域约-50 m等深线处布设计算点，提取波要素作为小范围计算的边界条件。工程水域外海-50 m深水处的波浪要素如表5所示。

以表5中各方向-50 m等深线波要素为边界条件，利用CGWAVE对小范围波浪场进行计算（图6）。

拟建码头为高桩梁板式码头，平面形式为开敞式，不同入射波向对拟建码头附近海域波浪情况有较大差异，为说明拟建码头处的波浪场分布情况，对NW向、NNW向、N向及NNE向4个入射波向对码头前沿波要素进行分析。

根据东福山岛拟建交通码头平面布置情况，在该交通码头平台前沿进行小范围波浪数学模型特征站位布置，由于码头平台设计长度为75 m，宽度为15 m，并考虑到码头所处水深，将特征站位站位的间距设置为8 m（图7）。

为统筹看待码头前沿波浪情况，对所布置的特征站位波浪要素计算结果提取并进行筛选，以码头前沿所布泊稳特征站位中波高最大站位为基准，按不同入射波向进行统计分析。各方向码头前沿波浪要素的统计结果见表6。

由图6波浪场分布情况及表6码头前沿波要素统计结果可以看出，NW、NNW、N及NNE 4个来向的外海波浪在向近岸传播过程中，都受到了不同程度的消耗。由于地形及岛屿的阻挡作用，NW及N向波浪在传播过程中波能消耗剧烈，传至码头前沿时H13%波高最高分别达到1.38 m和2.3 m；由于工程区域背靠东福山岛，NNE向入射波浪主要以绕射和折射方式传播，传至码头前沿时H13%波高最高达到2.19 m；NNW向入射波浪直面工程区域，波浪以较小的消耗传至码头前沿，H13%波高最高可达3.57 m。

表5-50 m等深线处的波要素统计Tab.5Wave parameters of-50 m depth contour

2 码头附近海域波要素计算分析

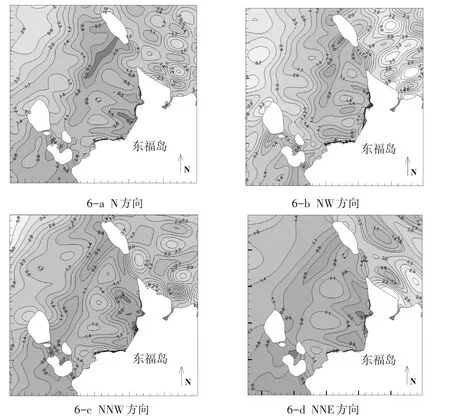
图6工程区域附近海域波浪场分布图Fig.6Distribution of wave field near engineering area

图7码头前沿波浪特征站位布置图Fig.7Characteristic stations of wave near the pier

表6码头前沿波浪要素统计Tab.6Wave parameters near the pier

3 结语

建立SWAN和CGWAVE大、小范围嵌套模型，对东福山岛交通码头附近海域波浪场进行计算。首先，利用SWAN模型进行大范围波浪计算，并以嵊山海洋站和普陀气象站的50 a一遇重现期波高进行了验证，结果表明该模型准确性较高，并开展了东福山岛外海相应方向的大范围波浪传播计算。

由大范围计算结果中提取等深线-50 m处波浪要素作为小范围计算边界条件，采用CGWAVE模型计算得到了东福山岛码头掩护区相应方向的波浪分布情况，并提取拟建码头前沿的波要素，其有效波高分别为1.38 m、3.57 m、2.3 m、2.19 m。SWAN模型与CGWAVE模型的联合应用，使得外海波浪由深海传至拟建码头掩护区过程中，大跨度地形下的波浪绕射、折射、反射等现象均得到了高精度的模拟，较好地反应了该海域的波浪场分布情况，表明该嵌套模型系统在实际工程中具有一定的实用价值。

［1］林祥志，王红川.漩门湾水域波浪计算分析［J］.水运工程,2004（7）:1-3. LIN X Z,WANG H C.Wave computation analysis at Xuanmenwan water area［J］.Port&Waterway Engineering,2004（7）:1-3.

［2］徐福敏.浅水波浪数值模型SWAN的原理及应用综述［J］.水科学进展,2004,15（4）:1-7. XU F M.Mechanism and application of a third generation wave model SWAN for shallow water［J］.Advance in water science,2004, 15（4）:1-7

［3］Pos J D,Kilner F A.Breakwater gap wave diffraction:An experimental and numerical study［J］.Harbor and Coast Engrg,1987,113（1）:1-21.

［4］Booij N,Holthuijsen L H,Ris R C.The SWAN wave model for shallow water［J］.Coastal Engineering Proceedings,1996,1（25）: 668-678.

［5］李绍武,梁超,庄茜.SWAN风浪成长模型在近海设计波浪要素推算中的应用［J］.港工技术,2012,49（2）:1-7. LI S W,LIANG C,ZHUANG Q.Application of SWAN model in onshore design wave factors calculation［J］.Port Engineering Tech⁃nology,2012,49（2）:1-7.

［6］王道龙.SWAN近岸海浪模式在辽东湾的应用［J］.海洋科学进展,2010,28（3）:1-6. WANG D L.Application of coastal wave model SWAN to Liaodong bay［J］.Advance in marine science,2010,28（3）:1-6.

［7］张宏伟.SWAN波浪模型在黄河三角洲海域的应用［J］.水运工程,2008（12）:1-5. ZHANG H W.Application of SWAN model at the sea area of the Yellow River delta［J］.Port&Waterway Engineering,2008（12）:1-5.

［8］Demirbilek Z,Panchang V.CGWAVE:A Coastal Surface Water Wave Model of the Mild Slope Equation［R］.Vicksburg MS:Army engineer waterways experiment station,1998.

［9］Dalrymple R A,Kirby J T,Hwang P A.Wave Diffraction due to areas of high energy dissipation［J］.Journal of Waterway,Port,Coast⁃al,and Ocean Engineering,1984,110（1）:67-79.

［10］ZHAO L Z,PANCHANG V G,CHEN W,et al.Simulation of wave breaking effects in two⁃dimensional elliptic harbor wave mod⁃els［J］.Coastal Engineering,2001,42（4）:359-373.

［11］LI R J,TAO J F.Analysis of Wave nonlinear dispersion relations［J］.China Ocean Engineering,2005,19（1）:167-174.

Combined application of SWAN and CGWAVE model in calculation of design wave parameters

WANG Shao⁃peng1,LI Rui⁃jie1,2,JI Ming3,DONG Xiao⁃tian1,ZHU Wen⁃jin4
（1.Key Laboratory of Coastal Disaster and Defence,Ministry of Education,Hohai University,Nanjing 210098, China;2.Laboratory of Ocean Environment,Hohai University,Nanjing 210098,China；3.Zhoushan Traffic Planning and Design Institute,Zhoushan 316021,China;4.Civil Engineering College,Huaihai Institute of Technology, Lianyungang 222006,China）

Taking the pier on Dongfushan island as an example,the distribution of the wave field around the protected area was simulated by the combined application of SWAN with CGWAVE model.Wave simulation of large scale area was carried out and the model was verified to be accurate.Then the wave parameters of-50 m depth contour were chosen from the large scale simulation results as the conditions for small scale wave simulation. The sea area near the pier was simulated by CGWAVE model,and the wave parameters in front of the pier extracted from the results were analyzed.It is found that combining SWAN with CGWAVE model together in design wave computation of Dongfushan pier has a good adaptability,providing important scientific basic and theoretical signifi⁃cance.

SWAN model;CGWAVE model;combined application;design wave parameters

TV139.2；TV131.61

A

1005-8443（2015）04-0308-08

2015-04-14；

2015-05-28

国家海洋局海洋公益性行业科研专项项目（201205005）；国家自然科学基金项目（41276017）；江苏省基础研究计划（自然科学基金）青年基金项目（BK20130409）；江苏省高校自然科学研究面上项目（13KJB570001）

王少朋（1988-），男，河北省邯郸市人，硕士研究生，主要从事物理海洋学方向研究。

Biography：WANG Shao⁃peng(1988-),male,master student.