桥梁结构地震响应与土层深度相关性研究

王典斌

(中国中铁二院科学技术研究院, 四川成都 610031)

桥梁结构地震响应与土层深度相关性研究

王典斌

(中国中铁二院科学技术研究院, 四川成都 610031)

由于土深在一定程度上影响着地震波的传播方式，并影响着地震波所包括的频谱特性。文章基于基岩设计反应谱来生成7条人工地震波，通过不同土层深度的一维传动后作为桥梁结构的地震输入，来研究土层深度对场地放大系数与位移修正系数的影响，并通过数值分析来研究不同土深情况下的桥梁的非线性位移反应的变化，并与规范值进行了比较，得到了以下结论：对于不同的位移延性水平，位移修正系数计算结果在短周期范围内差别较大，而在长周期范围内，土的深度对位移修正系数产生了一定的影响。场地放大系数会随着土深的增加而改变峰值所对应的周期。随着土深增加，非线性位移反应总体呈增大趋势。

地震响应； 桥梁结构； 场地放大系数； 位移修正系数

众所周知，土是地震波的传播过程中的介质，它能够深刻地影响基岩地震波的性质，且能对结构在地震作用下的性能产生影响。在很多的设计规范里面，土对地震波的影响经常使用场地放大系数来表示，场地放大系数的取值则跟场地的划分息息相关。而针对场地的划分，国外规范一般使用地表以下30 m范围内的土层平均剪切波速剪这个指标来进行。在我国，基本使用覆盖层厚度与20 m两者的较小值范围内的土层的平均剪切波速来进行。然而，很多学者指出仅仅用土层的平均剪切波速去表征场地的放大系数可能会导致场地放大系数的错误估算，因而在这一过程中，需要考虑多个参数对其的影响，比如土层的深度与周期的影响。近年来，学界开始注意这类问题，新西兰规范与日本规范将场地的基本周期作为一个区分场地的指标，由于周期与土层厚度直接相关，因而也是间接考虑了土的深度的影响。Rodriguez-Mark等人[1]则认为需要将土的深度考虑到场地的划分中，并提出了将土的深度与厚度并用。Pitilakis等人[2]为欧洲规范提出了一套新的场地划分标准，在这套新的标准中，他们将土的深度与其他指标联用来到达划分场地的目的。

在过去的十几年里面，桥梁结构的抗震设计方法从开始的基于强度的抗震设计思路到最近的基于位移与基于性能的抗震设计方法。基于位移的设计强调的是对结构位移的控制。在大多数规范中，一般基于等位移原理或等能量原理，使用弹性反应谱来估算结构的非线性位移。在使用等能量原理时，需要使用位移修正系数Rd来得到桥梁结构的非线性位移。然而，很少研究土的深度对位移修正系数的影响以及对桥梁结构非线性位移响应的影响。

因而，在本文中，将基岩设计反应谱来生成7条人工地震波，通过土层的一维传动后作为地震输入，研究对场地放大系数与位移修正系数的影响，从而来分析桥梁的非线性反应，并与规范值进行了比较。需要注意的是在本文的分析中，忽略了土层介质之间的阻抗差，需要注意的是土层介质之间的阻抗差对场地放大系数有较大的影响。且以一座桥梁结构为例，来研究土的深度对结构非线性位移的影响。

1 场地与桥梁结构

在本文中，选择了某中部三类场地进行分析，该场地位于北纬34°，东经114°。在分析场地放大系数与位移修正系数时，取常遇水准100 a超越概率63 %(对应PGA 0.05g)的设计反应谱来生成所需的7条地震波，在计算桥梁结构的非线性响应时，则用了罕遇水准50 a 2 %的设计反应谱来进行分析。图1给出了7条人工地震波与设计反应谱拟合的情况。

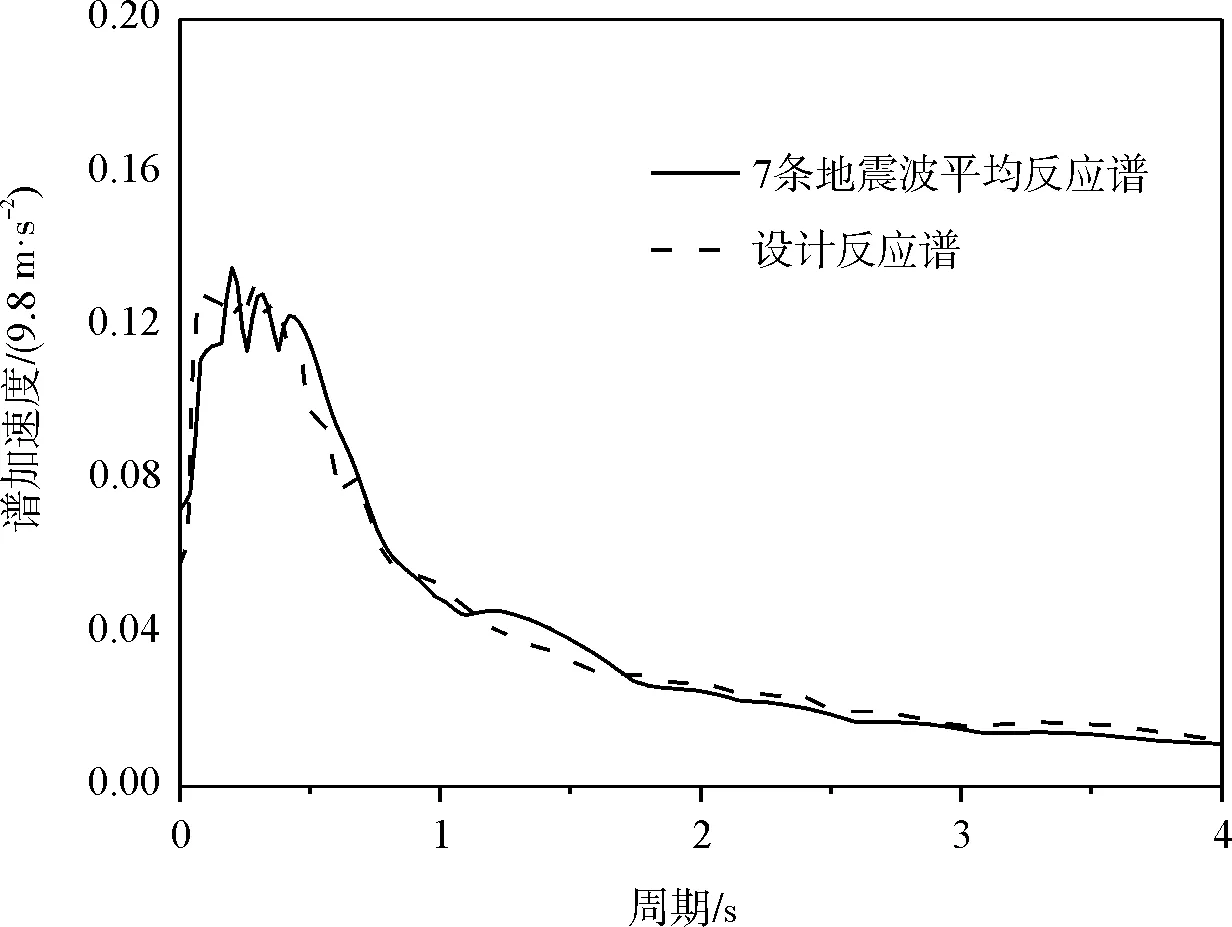
图1 7条人工地震波与设计反应谱的拟合

对于场地的地震非线性分析而言，一般需要定义土的剪切模量、阻尼以及塑性指标等影响土体地震反应的变量。在本文中，填土与沙子(前20 m)则使用Seed与Idriss等[3]给出的剪切模量折减与阻尼曲线，黏土(后180 m)则采用Vucetic与Dobry等[4]给出的塑性指标曲线。图2给出了相应的土层深度，单位自重以及剪切波速。本文将使用SHAKE2000来进行分析。SHAKE2000能进行一维的等效线性化的场地的地震响应分析。

本文所考虑的连续刚构桥梁结构总长174 m，跨径布置为(50+74+50) m，墩高38 m，墩采用，主梁采用箱形截面，上顶板宽7 m，厚0.28 m，腹板厚度跨中是0.4 m，支点处为0.6 m，图3给出了具体的尺寸与布置。桥梁的主梁与墩单元均采用弹性梁单元模拟，桥台上布置滑动支座，摩擦系数为0.02，且桥台处采用大刚度固结处理。墩底固结，未考虑桩土相互作用对桥梁结构的影响。模型采用软件OpenSees建立，桥梁的动力特性可见表1。

图2 土层深度、单位自重以及剪切波速

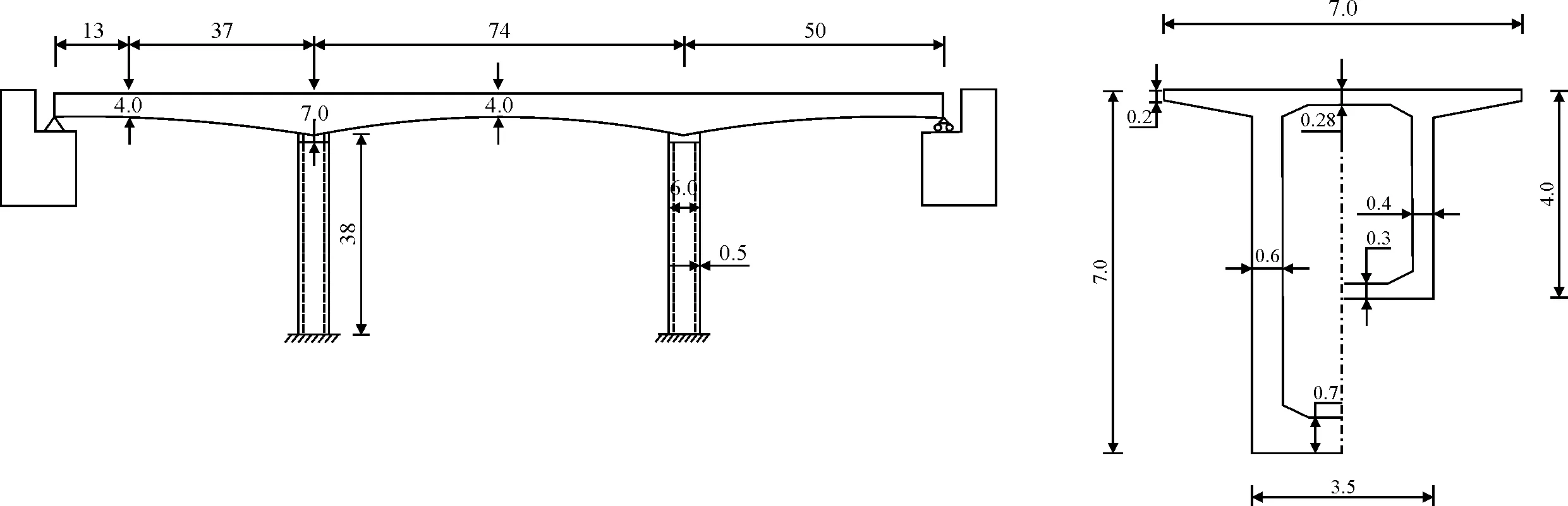
图3 桥梁结构具体尺寸与布局

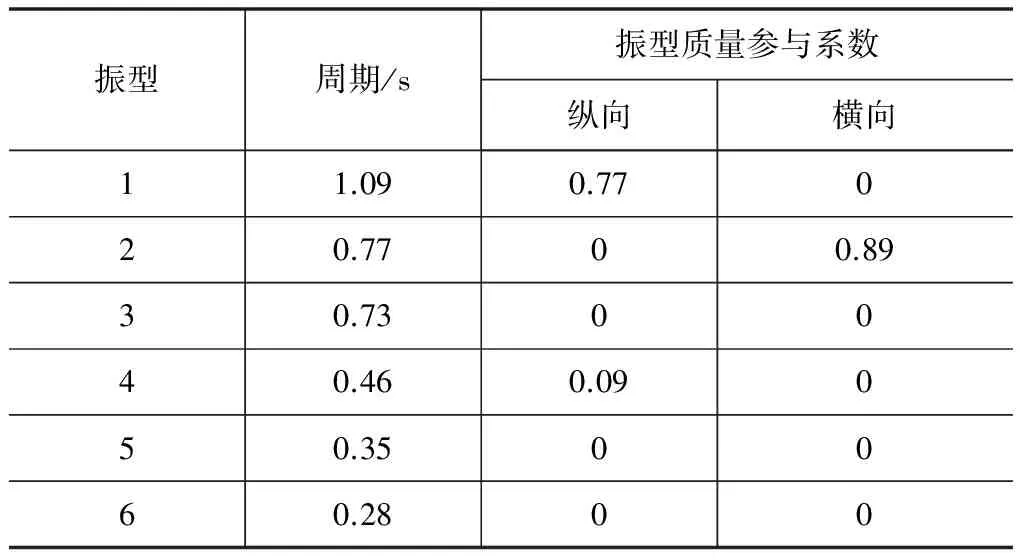
振型周期/s振型质量参与系数纵向横向11．090．77020．7700．8930．730040．460．09050．350060．2800

2 土的深度对场地放大系数的影响

在本文中，场地放大系数采用地表谱加速度值与基岩谱加速度值的比值来表示。图4与图5给出了不同土深下的地表的反应谱与场地放大系数。从图4中可以看出，不同的土深会导致地表反应谱的峰值以及形状的改变，且反应谱所对应的周期也发生了改变，这可能跟不同土层的自身频率影响地震波的频谱有关。从图4中还可以看出，仅对短周期而言，土深的增加并不一定增加了地表波的谱加速度，而对于长周期(大于1 s)而言，土深的增加在一定程度上增加了谱加速度。从图5中可以看出，场地放大系数会随着土深的增加而改变峰值所对应的周期，这点跟上文的谱加速度类似，也与土层自身的频率有关。对于规范值，本文参考了美国规范的定义，针对本文所用的三类场地，在美国规范中为类似的D类场地而计算，从计算的结果来看，规范的值是偏保守的。

图4 不同土深下的地表反应谱值

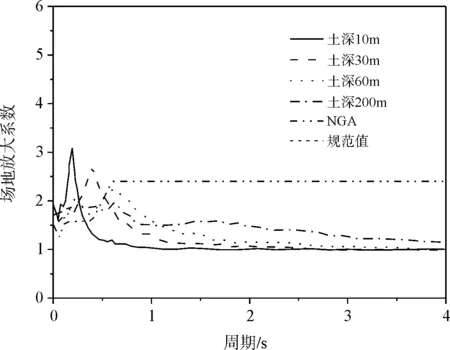
图5 不同土深下的场地放大系数

3 土的深度对位移修正系数的影响

位移修正系数Rd的定义是，在给定的周期T下，非线性位移谱值与线性位移谱值的比值。有了位移修正系数Rd，可以直接由规范中的常规线性设计反应谱的结果得到结构的非线性反应。

(1)

图6给出了所考虑的场地的位移修正系数的平均值，所使用的七条地震波均与目标谱拟合，且地震波的峰值加速度(PGA)为0.05g，并在计算中考虑两个水准的位移延性水平(μ=2，6)，初始阻尼取为5%。非线性位移谱采用软件BISPEC计算。由于滞回模型在一定程度上会影响结构的非线性反应和位移，因而本文选择了理想弹塑性模型，并与Miranda[5]提出的经验模型进行了比较，Miranda模型可由下式表示：

(2)

其中系数C1和系数C2分别与位移延性比μ和场地类别有关，在本文中，取值分别为12和0.8。

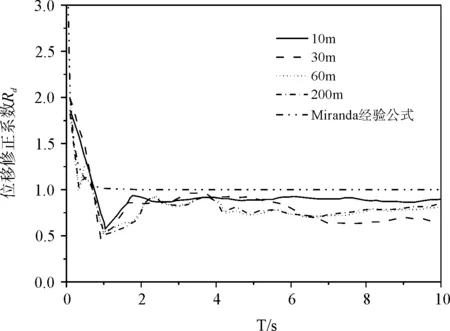
图6 不同位移延性水平下的位移修正系数

从图6上可以看出，对于不同的位移延性水平，Rd的数值计算结果在短周期范围内差别较大，特别是在周期较小的时候。另外，Rd的数值在场地的周期附近出现了极值，这也说明很多规范要将所考虑的场地的周期考虑进去的原因。在中周期范围内，Rd的数值计算结果与经验公式的差距不大，且随着土层的加深，Rd的数值并未发生变化。而在长周期范围内，土的深度对Rd的数值产生了一定的影响，当位移延性水平不高时，土的深度的影响有限，然而当位移延性水平提高时，在6 s以前土深越大，影响越大，6 s以后，30 m土深反而影响更大。

4 结构非线性地震反应

本节将研究土层深度对结构地震非线性位移响应的影响，并且对现行设计规范[6,7]的计算值与国外学者Cadet等[8]提出的SAPE模型进行比较。在进行数值计算时，本文采用的方法是根据软件BISPEC得到非线性反应谱进行反应谱分析。对于规范方法而言，由于目前国内外现行的规范都是基于位移的抗震设计方法，在基于位移的抗震设计方法中，经常使用位移修正方法(DMM)来计算结构的非线性位移。在DMM方法中，结构关键节点的非线性位移位移(一般就是结构的最大位移)可以用式(3)来计算：

(3)

式中:Te为基本周期，C0是将多自由度体系位移等效为单自由度体系位移时的修正系数。对于桥梁结构而言其他结构而言，C0值可以通过式(4)计算：

(4)

式中:Г表示第一阶周期所对应的振型参与系数，φcritical表示关键节点的振型分量，本文中，关键节点取为最大位移点。式(3)中Rd表示线弹性位移转化为最大非线性位移估计值的修正系数，可以用式(5)计算：

(5)

式中：a表示场地类型系数，本文可取为60，R表示位移延性比。当基本周期大于1 s时，Rd值取1。式(3)中Ch表示循环刚度退化效应的修正系数。当周期大于0.7 s时，值也取为1。

表2给出了通过式(3)计算的本文所考虑桥梁结构的非线性位移反应。从表中可以看出，随着土的深度增加，非线性位移反应在总体趋势上是增大的。且不同的PGA值所得到的非线性响应不同。从表2中，还可以看出，当土深不超过30 m时，规范值是比较保守的，但当土深超过30 m时，规范值是低估了应有的非线性位移反应。另外，SAPE模型所得到的非线性位移值普遍偏高于实际数值计算值。

表2 桥梁结构的非线性位移反应

5 结论

本文基于基岩设计反应谱来生成7条人工地震波，通过不同土层深度的一维传动后作为桥梁结构的地震输入，来研究土层深度对场地放大系数与位移修正系数的影响，并通过数值分析来研究不同土深情况下的桥梁的非线性位移反应的变化，并与规范值进行了比较，得到了以下结论：

(1)对于不同的位移延性水平，Rd的数值计算结果在短周期范围内差别较大，而在长周期范围内，土的深度对Rd的数值产生了一定的影响。

(2)场地放大系数会随着土深的增加而改变峰值所对应的周期。

(3)随着土的深度增加，非线性位移反应在总体趋势上是增大的。当土深小于30 m时，规范值是比较保守的，而当土深大于30 m时，规范值则低估了实际的非线性位移反应。

[1] Rodriguez-Marek A, Bray JD, Abahamson NA. An empirical geotechnicalseismic site response procedure. Earthquake Spectra. 2001, 17:65-87

[2] Pitilakis K, Riga E, Anastasiadis A. Newcode site classification, amplificationfactors and normalized response spectra based on a worldwide ground-motion database. Bull Earthquake Eng. 2013, 11(4):925-66

[3] Seed, H. B. and Idriss, I. M. [1970] “Soil moduli and damping factors for dynamic response analysis,”Technical Report EERC 70-10, University of California, Berkeley

[4] Vucetic, M. and Dobry, R. [1991] “Effect of soil plasticity on cyclic response,” Journal ofGeotechnical Engineering, 117(1), 89-107

[5] Miranda E. Inelastic displacement ratios for structures on firm sites. J StructEng ASCE, 2000, 126(10)

[6] CJJ 166-2011城市桥梁抗震设计规范[S]

[7] JTG/T B02-01-2008 公路桥梁抗震设计细则[S]

[8] Cadet H, Bard P-Y, Duval AM, Bertrand E. Site effect assessment using KiK-netdata: Part 2- Site amplification prediction equation based on f0and Vsz. BullEarthquake Eng, 2012, 10(2):451-89

王典斌(1981～)，工程师。

U442.5+5

A

[定稿日期]2015-03-16