Hoek－Brown准则下岩质边坡浅层稳定性分析

龙姣云

（永州市公路桥梁建设有限公司，湖南永州 425000）

随着公路建设事业在中国中西部山区的发展，高砌坡和陡峭岩质边坡在高速公路中的使用越来越普遍。工程中对此类岩质边坡需进行稳定性验算，必要时需进行工程防护，以保证其整体安全。田小甫［1］等人采用数值模拟的方法，对含有结构面的岩质边坡进行了地震作用影响下数值模拟研究。赵洪宝［2］针对某露天矿开挖形成的岩质边坡，利用有限差分软件FLAC3D，对边坡体开挖方向上的应力演化和变形规律进行了研究。段永伟［3］等人以顺层岩质边坡为研究对象，运用不平衡推力法、Sarma法及直线型分方法，对边坡的稳定性进行了分析，并与实际结构特征和破坏情况进行了比较。相关研究大多利用数值模拟或者极限平衡方法，进行岩质边坡整体稳定性分析。而对于某些中、强风化的岩质边坡，由于表面岩体受风化和剥落作用较为明显，使其强度降低，常发生浅层破坏，造成局部落石甚至崩塌，威胁着交通和行车安全。因此，对该类岩质边坡进行浅层稳定性分析在工程中是十分必要的。

作者拟利用塑性力学中的极限分析方法，采用广义Hoek－Brown准则，对中、强风化岩质边坡的浅层稳定性进行分析。以期为工程计算提供一种新的思路和理论计算方法。

1 广义Hoek－Brown准则下的极限分析

对边坡等岩土构筑物进行稳定性分析时，强度准则选取的准确与否，直接关系到分析结果的可靠性。在对土质边坡进行分析时，常采用线性Mohr－Coulomb破坏准则。而对于岩质边坡，由于岩体自身复杂的应力、应变特性，线性Mohr－Coulomb破坏准则常无法准确描述其物理力学性质。另一方面，不同类别岩体由于其自身结构特性的差异，力学性质也有较大差别，同样关系到破坏准则的选择。

Hoek［5］等人在大量室内三轴试验以及现场测试的基础上，提出了Hoek－Brown强度准则。该准则考虑了岩体结构和强度等多种因素的影响，适用于多节理裂隙岩体以及含有均匀的等规模、间距和强度的结构面岩体。对于节理和裂隙较为发育的中、强风化岩体，Hoek－Brown准则能够较好地表达其力学特性。在实际应用过程中发现：当岩体的地质强度指标GSI＝25时，Hoek－Brown准则中的计算参数会出现突变。为了克服这个缺点，经过不断的补充和修正，2002年Hoek又提出了最新的广义Hoek－Brown准则［6］，其表达式为：

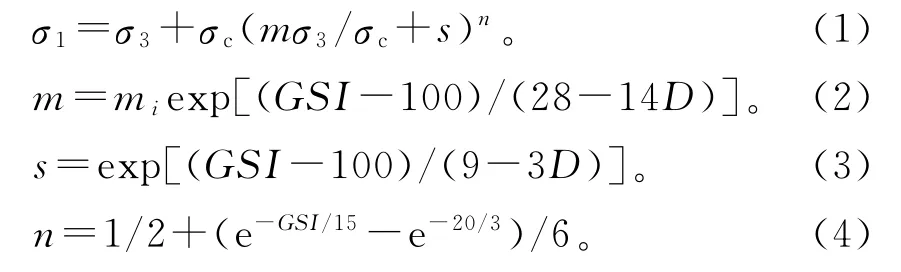
式中：σ1为岩石的最大主应力；σc为完整岩体的单轴抗压强度；σ3为岩石的最小主应力；D为岩石扰动因子；mi为完整岩块的Hoek－Brown常数；GSI为地质强度指标（根据岩体所处的地质环境，岩体结构特性和表面特性来确定）。

在Hoek－Brown准则中，抗剪强度的包络线是非线性的，而传统的极限分析方法建立在线型的Mohr－Coulomb破坏准则上。因此，在利用极限分析计算Hoek－Brown准则下的岩体稳定性时，需要采用切线法［7－8］，如图1所示。即在Hoek－Brown破坏包络线上任取一点C作切线，该切线与τ轴的截距为c，其斜率为tanφ，图中c为粘聚力，φ为内摩擦角。由于不同正应力σn下切线的斜率不同，导致c和φ的不同，因此c，φ不是常量而是瞬时值，它们的关系式为：

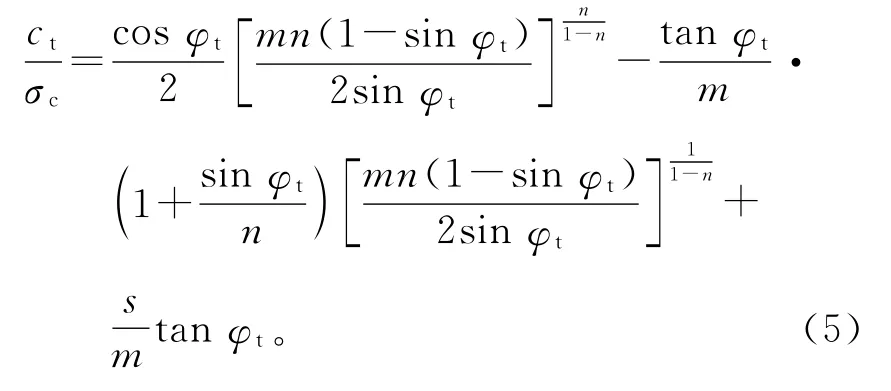
式（5）可记为ct＝σcf0（φt）。式中非线性抗剪强度指标φt在上限计算时为未知参数，ct在φt确定后由式（5）求得，两者最终的取值通过能耗最小原理进行优化求得。

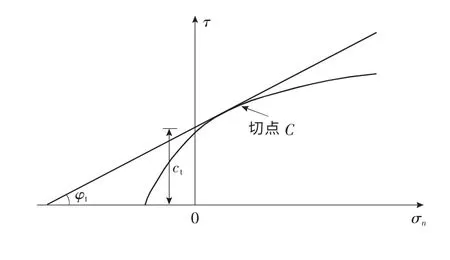
图1 极限分析中Hoek－Brown准则的切线法Fig.1 Tangent method of Hoek－Brown failure criterion in limit analysis

2 破坏机构的建立

对于中、强风化的岩质边坡，其表面长期受风化和雨水冲刷等自然侵蚀作用，岩体破碎，节理和裂隙发育。相比边坡内部岩体强度大幅降低，因此在岩质边坡的浅层破碎带中，易产生浅层破裂面，从而导致崩塌或者落石（如图2所示）。因此，有必要对中、强风化边坡进行浅层稳定性分析。

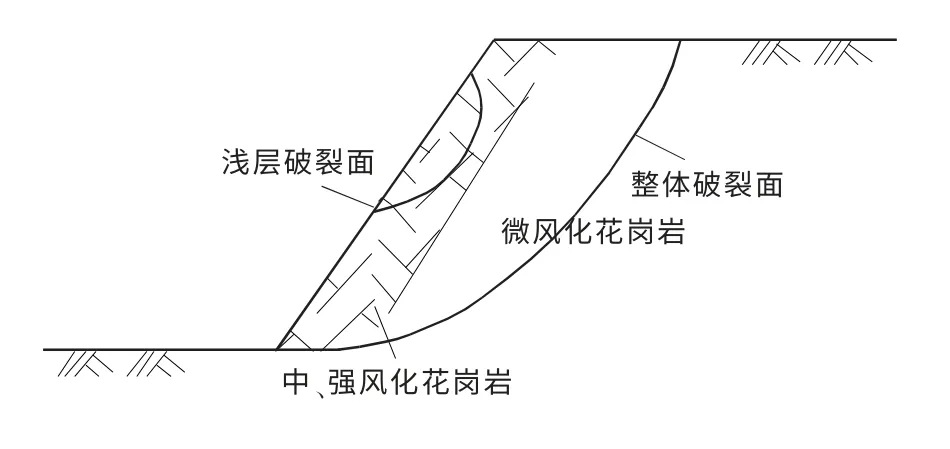
图2 岩质边坡的整体破坏和浅层破坏Fig.2 General and shallow failure for rock slope

利用上限定理，针对岩质边坡的浅层滑动，建立了由旋转刚体组成的破坏机构，如图3所示。其中滑裂面AB的方程为对数螺旋线［9］：

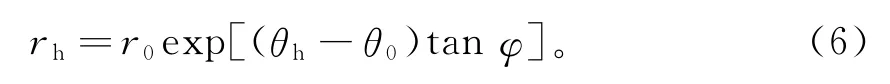
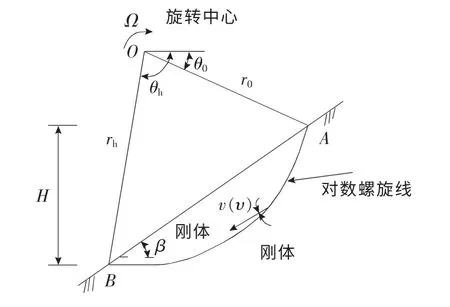
图3 岩质边坡浅层滑裂时的破坏机构Fig.3 Failure mechanism of shallow sliding for rock slope

由几何关系可得：

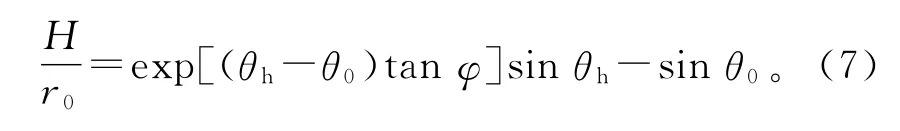
式中：H为临界高度。

由重力提供外力功率：

式中：γ为土体重度；Ω为刚体旋转的角速度。

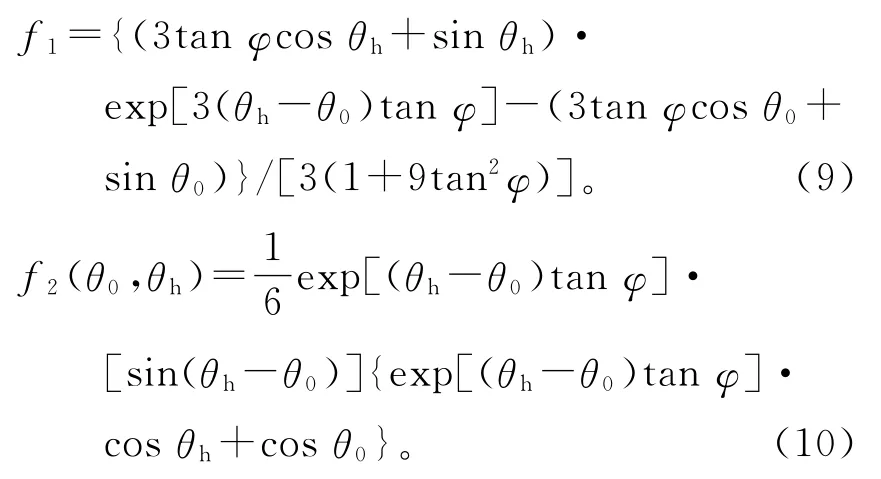
内部能量耗散D发生在速度间断面上。

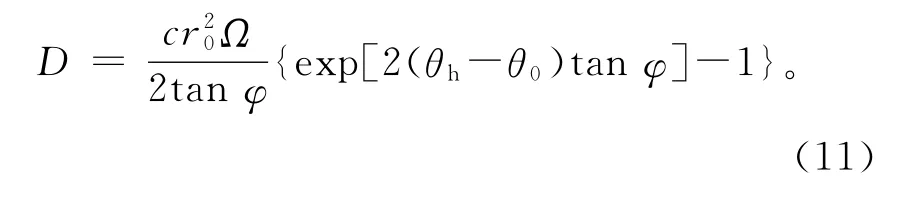
令破坏机构的内部能量耗散等于外力做的功，所确定的边坡高度H即为上限高度。

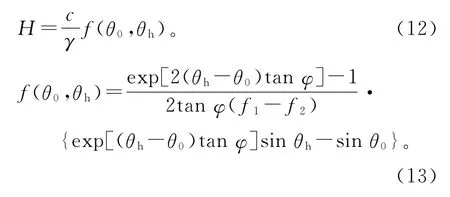
在Hoek－Bown准则下应用上限定理时，需将式（12）中的c和φ用瞬时的切线抗剪强度ct和φt替换。由几何关系可得：

结合式（11），（14）和（5），岩质边坡浅层滑动可表示为约束条件下的多变量非线性规划问题：

3 结果分析

在计算中，对边坡稳定性的评价指标是临界高度H，而在极限平衡或者数值模拟方法中，常用的评价指标为安全系数Fs。为了便于与已有方法进行比较以及更方便的工程应用，运用强度折减技术，在式（15）的基础上进行安全系数的求解。由强度折减法可得：

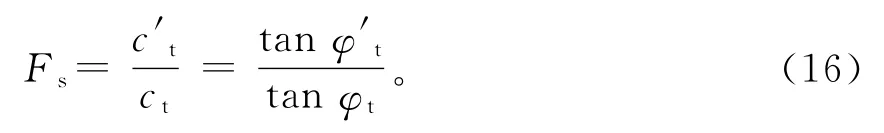
式中：c′t与tanφ′t均为边坡处于临界状态的抗剪强度参数。

将式（16）代入式（15），即可得到岩质边坡浅层滑动时的安全系数方程：

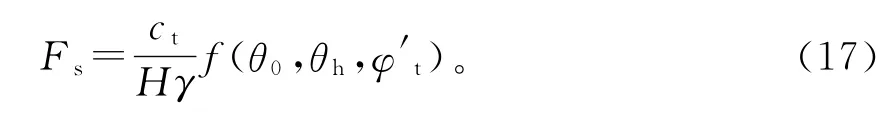
式中：H为已有边坡的高度，φt＝arctan（tanφt／Fs）。

因式（17）等号两边均含有Fs的项，因此该式是关于Fs的隐函数方程，只能利用序列二次规划算法等数值方法进行求解，部分计算结果如图4所示。从图4中可知，不同坡角和边坡高度下，边坡浅层滑动的安全系数随着GSI的变化规律。在图4（a）中，H＝25m，其他计算参数为mi＝10，γ＝26kN／m3，σc＝40.0MPa。图4（b）中β＝60°，其余参数同图4（a）。从图4中可以看出，随着GSI的增大，边坡的浅层稳定性也不断增加。

图4 岩质边坡浅层安全系数的变化Fig.4 Variation for shallow safety factor of rock slope

4 工程实例

塔山二号隧道位于207双牌尚仁里至道县县城段公路改建工程第ⅢA3合同段。在隧道进洞初期，道县端洞口K109＋915～K109＋945段路基的线路左侧边坡发生了数次边坡坍塌。其正面视图如图5所示。道路左侧的岩质边坡为多级台阶边坡组成，其中最低一级边坡的坡率为1∶0.3，台阶高度为12m，其岩体为节理发育的强风化花岗岩。根据室内试验结果，其强度参数为mi＝5，H＝12m，γ＝22.4kN／m3，σc＝30.0MPa。采用本研究提出的方法对其局部稳定性进行了分析，得到了安全系数Fs＝0.83，因此，需要对其进行加固。对于加固后的边坡方案，也可以采用极限分析方法进行稳定性分析，但是，由于其假设滑动面穿过锚杆加固段，因此，在建立破坏机构并进行内、外功率的计算时，需要考虑锚杆内部的能量耗散［10］。

图5 塔山二号隧道道县端洞口Fig.5 Tunnel entrance of Tashan 2＃Tunnel forward to Dao country

5 结论

对于表面节理发育的岩质边坡，需要在Hoek－Brwon准则下分析其浅层稳定性，以确保工程安全。本研究基于极限分析上限定理，建立了适用于浅层滑动的破坏机构，并推导了岩质边坡浅层滑动的安全系数表达式。工程计算的结果表明，该表达式能够评估岩质边坡的稳定性，指导工程应用。

（References）：

［1］田小甫，孙进忠，刘立鹏，等.结构面对岩质边坡地震动影响的数值模拟研究［J］.地质与勘探，2012，48（4）：840－846.（TIAN Xiao－fu，SUN Jin－zhong，LIU Li－peng，et al.Numerical simulation of the influence of structural planes on seismic motion on rock slopes［J］.Geology and Exploration，2012，48（4）：840－846.（in Chinese））

［2］赵洪宝，潘卫东.开挖对岩质边坡稳定性影响的数值模拟［J］.金属矿山，2011，421（7）：32－35.（ZHAO Hong－bao，PAN Wei－dong.Numerical simulation of the impact of excavation on the stability of rock slope［J］.Metal Mine，2011，421（7）：32－35.（in Chinese））

［3］段永伟，胡修文，吁燃，等.顺层岩质边坡稳定性极限平衡分析方法比较研究［J］.长江科学院院报，2013，30（12）：65－68.（DUAN Yong－wei，HU Xiu－wen，YU Ran，et al.Comparative study on limit equilibrium methods for stability analysis of bedding rock slope［J］.Journal of Yangtze River Scientific Research Institute，2013，30（12）：65－68.（in Chinese））

［4］潘勤学，查旭东，杨博.岩质路堑边坡柔性支护系统防护性能分析［J］.中外公路，2014，34（5）：19－22.（PAN Qin－xue，ZHA Xu－dong，YANG Bo.Protection propterty of flexible supporting system for rock cutting slope［J］.Journal of China ＆Foreign Highway，2014，34（5）：19－22.（in Chinese））

［5］Hoek E，Brown E T.Empirical strength criterion for rock masses［J］.Journal of the Geotechnical Engineering Division，1980，106（9）：1013－1035.

［6］Hoek E，Carranza－Torres C，Corkum B.Hoek－Brown failure criterion－2002edition［A］.Proceedings of NARMS－TAC Conference［C］.Toronto：University of Toronto Press，2002：267－273.

［7］Yang Xiaoli，Yin Jianhua.Slope stability analysis with non－linear failure criterion［J］.Journal of Engineering Mechanies，2004，130：267－273.

［8］Yang Xiaoli，Yin Jianhua.Stability faetors for rock slopes subjected to pore water pressure based on the Hoek－Brown failure criterion［J］.Roek Mechanics ＆Mining Sciences，2006，43：8146－1152.

［9］Chen W F.Limit analysis and soil plasticity［M］.Amsterdam：Elsevier，1975.

［10］赵炼恒，李亮，杨峰.加筋土坡动态稳定性拟静力分析［J］.岩石力学与工程学报，2009，28（9）：1904－1917.（ZHAO Lian－heng，LI Liang，YANG Feng.Dynamic stability pseudo－static analysis of reinforcement soil slopes［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（9）：1904－1917.（in Chinese））