旋流竖井泄洪洞数值模拟研究
代双键
(重庆市水利电力建筑勘测设计研究院,重庆 400020)
旋流竖井泄洪洞数值模拟研究
代双键
(重庆市水利电力建筑勘测设计研究院,重庆 400020)
通过对旋流竖井内水体的数值计算,将常规水力学参数计算结果与试验结果进行对比分析后发现,数值计算在研究旋流竖井泄洪洞的涡腔形态、沿程水深及壁面压强等方面可以得到与试验研究相一致的结果,因此,可以认为:竖井沿程流速计算值也同样与实验结果具有良好的吻合度,从而有效解决了模型试验难以准确测量流速的问题。
旋流竖井;数学模型;网格划分;结果的比较
0 引 言
旋流竖井泄洪洞由于其具有受地质地形条件限制较小、修建难度相对较低、消能效果突出以及出口布置方式灵活等特点,越来越受到水利水电工程界的关注。尤其是随着当前我国正处于水电建设事业的井喷式发展阶段,许多高水头、大流量、深峡谷的高坝大库正在建设或者处于规划阶段,在常规泄水建筑物无法良好地实现泄洪消能的情况下,旋流竖井作为一种新兴发展的泄洪消能建筑物不失为一种良好的选择。
目前,学术界对于旋流竖井泄洪洞的探究已相对比较深入,一些学者通过具有一定比尺的物理模型对其进行了研究[1-5],另外一些学者则通过物理模型同时辅以数值计算的方式[6-9]来分析旋流竖井泄洪洞沿程各项水力学参数,对旋流竖井泄洪洞的基本流态、泄流能力、壁面压强分布特性、涡腔需气量以及消能率等都有了一定的认识,同时也据此总结出了一些对于竖井沿程涡室直径、收缩段尺寸以及竖井直段高度等旋流竖井结构参数的设计参考公式。由于实验测量手段的局限性以及旋流竖井内水流流态的复杂性,物理模型试验在目前的技术手段下很难获得准确的流场数据,这使得数值模拟计算的优势得以充分地发挥。本文采用了物理模型试验和数值模拟相结合的手段,对旋流竖井内部水流流态、沿程壁面压强分布以及流速等水力学参数进行了详细的描述。
1 数学模型
本文采用标准k-ε双方程紊流模型,该紊流模型对雷诺应力各分量采用各向同性假设。目前双方程模型在实际工程和科研中使用较多,标准的k-ε模型比零方程和单方程模型有了很大的改进,在工程实际中得到了较为广泛的应用和验证,它考虑了紊动速度比尺和紊动长度比尺的输运。对于大多数水流问题,标准双方程模型能得到较为满意的结果。对于不可压非定常流,标准k-ε紊流模型的连续方程、动量方程和k、ε方程分别为:
动量方程:

k方程:
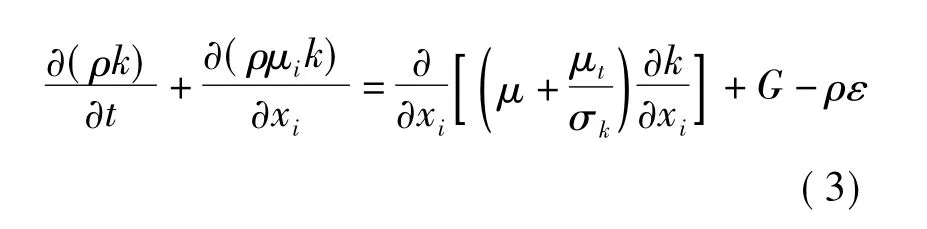

式中 ρ和μ分别为体积分数平均的密度和分子粘性系数。P为修正压力;μt为紊流粘性系数,它可由紊动能k和紊动耗散率ε求出:

式中 Cμ为经验常数,Cμ取0.09。
σk和σε分别是k和ε的紊流普朗特数,σk=1.0,σε=1.3。C1ε和C2ε为 ε方程常数,C1ε= 1.44,C2ε=1.92。G为由平均流速梯度引起的紊动能产生项,它可以由下式定义:

引入水气分层两相流的VOF[10]模型后,在控制体内对第q相流体的容积分数规定为:αq=0表示控制体内无q相流体;αq=1表示控制体内充满q相流体;0<αq<1表示控制体内部分充满q相流体,对所有流体的容积分数总和为1,即:∑αq=1。在水气分层两相流中,αω为水的体积分数,αa为气的体积分数,αω+αa=1,ρ和μ就是体积分数的函数,而不是一个常数。它们可由下式表示:

式中 ρω和分别是水和气的密度;μω和μa分别是水和气的分子粘性系数,通过对水的体积分数αω的迭代求解,ρ和μ都可以由式(7)、(8)求出。
2 计算体型及网格划分
数学模型模拟范围从短有压进口前50 m,包括旋流式竖井泄洪洞的上平段、涡室、竖井、压坡段及下平段。一般来讲网格越细计算结果精度就越高,但过细的网格就意味着占用的内存资源就越大,其所需计算时长也越长。为节省计算时长,空间网格剖分采用非均匀网格,上平段、竖井及下平段等计算精度要求相对较低区域的网格较为稀疏而涡室内的小挑坎附近、竖井与压坡处网格较密,网格尺度的变化范围0.08 m~4 m。
采用控制容积法[11]对偏微分方程组进行离散,压力-速度耦合采用PISO算法。由于计算的下游出流位置流动已基本发展成稳定状态,可给定在出流边界上的法向梯度为零,即:∂v/∂x=0,∂k/∂x=0,∂ε/∂x=0;在固壁上给定法向的速度为零和无滑移条件,近壁的黏性底层采用壁函数法[11]处理。整个计算区域如图1所示,水流入口采用速度入口边界条件,根据模型试验得到引水道入口断面水深及流量(Q=1 200 m3/s),由此可知入口法向速度vn=1.32 m/s,出口及所有的气体边界均采用压力边界条件,压力为大气压值。

图1 数学模型计算域
3 计算结果与试验结果的比较
模型结合某水电站工程进行,试验采用单体正态水工模型,水流流量为1 200 m3/s,模型试验比尺为1∶40,按重力相似准则设计,模拟范围包括短有压进口并向上游区域延伸50 m作为模拟库区、上平段、涡室、收缩段、竖井段、出口压坡以及一定长度的下平段,采用有机玻璃制作。
试验量测内容主要为上平段沿程水深以及竖井壁面沿程压强等,并对水流流态进行了详细的观测。在上平段底板中轴线位置沿程布置24个测压点,在竖井沿程壁面不同高程环向分别布置4个测压点,一共96个测点,出口压坡设置14个测点,压强采用测压管以水柱高度的方式测量。
3.1 上平段沿程水深及涡室、竖井段空腔形态
采用VOF方法的标准k-ε双方程紊流数值模型能够很好地模拟旋流竖井的上平段、涡室、收缩段、竖井直段、下平段各部位的水面线。图2为旋流竖井上平段沿程水深的计算值与试验值对比图,可以看到,上平段沿程水深的试验值与计算结果吻合较好,沿程水面波动较小,水流流态平顺,这对于顺直水流进入竖井内部实现流速的良好转向有积极作用。

图2 计算水面与试验值对比
图3为竖井中轴线纵剖图以及不同高程处竖井横剖面的空腔形态图(图中h表示距离竖井底板的高度),可以看到,竖井上部沿程空腔形态良好,直至下部水垫表面均保持了持续稳定的空腔形态,这对于竖井沿程的水流掺气有着积极的作用;竖井底部被水体所充满,上部发生环状水跃,位置处于h=46 m~50 m区间,通过涡室起旋并呈螺旋状贴壁运动至此的水体在消能水垫内通过环状水跃进行充分的消能;另外,随着高程的逐渐降低,竖井壁面水深在收缩段时有所增加,这是由于受到收缩段内径的逐渐减小的影响,过流断面束窄所致,而在竖井直段除底部消能水垫外其沿程壁面水深没有较大的变化,这主要是因为随着高程的降低,减小的势能主要转化成了动能,而对水体的压强贡献较小。

图3 竖井空腔形态
3.2 壁面压强分布特性
过流壁面的压强分布特性是数值计算和物理模型试验中重要的水力参数之一,通过压强的分布特点,可以判定在水工建筑物中可能会出现空化空蚀现象以及出现的部位,从而可以由针对性地进行加固防护或者设置掺气设施等。图4描述了各部位壁面压强的分布特性以及试验值与计算值的对比,可以看到,二者具有较好的吻合性,但是在某些突变的位置存在较大的差异,分析认为出现这种状况的主要原因是:模型试验中物理模型是由多个部分拼接安装而成,而不是像数值模拟一般是一个完整的整体,在接口处可能存在没有处理好的异常“突起”,水流经过这些“突起”时,就会出现脱壁现象。
在竖井上部涡室段,出现了一个较大的压强峰值,这是由于从上平段与涡室连接的位置水流出现较大程度地转向,动能转换成压能所致,这从上节流态图中也可以清晰地看到,水体在该位置聚集并逐渐由原来的直线运动转换成具有一定旋转速度的螺旋流;竖井直段上部区域压强变化相对较小,这跟上节水深的变化趋势相对应,即势能的降低在该区段主要转化成了动能,而在竖井直段下部区域压强则明显增大,这是由于下部水垫的存在使得流速急剧降低并实现转向,从而使得压强大幅增大。
压坡段压强计算值与试验值吻合良好,沿程呈现逐渐较小的趋势,经过竖井底部水垫的消能以及转向的水体完全充满压坡,该段较大的压强保证了压坡具有足够小的空蚀空化破坏风险。
3.3 竖井沿程流速分布特性
从上文可以看到,上平段水深以及竖井沿程压强的数值计算结果与试验值吻合较好,因此可以认为流速的数值计算结果与试验值也具有一致性。由于竖井体型的特殊性,模型试验中很难准确测得其内部各点的流速值,而数值计算提供了一个良好的解决方案。图5为不同高程时竖井沿程流速分布,可以看到在竖井底部,由于发生了强烈的紊动剪切消能,水流速度相对较小,随着高程的逐渐增加,流速逐渐增加,至h=47 m位置附近,水流速度达到最大值约为30 m/s左右,之后高程再继续增加,水流速度逐渐减小。分析可知,在流速出现最大值位置以上区域随着高程降低,流速逐渐增大的原因是势能转化为动能所致,而在该位置以下流速又出现逐渐降低的趋势,则是由于下部消能水垫的消能作用,环状水跃延伸至该处,使得流速降低,压强增大。
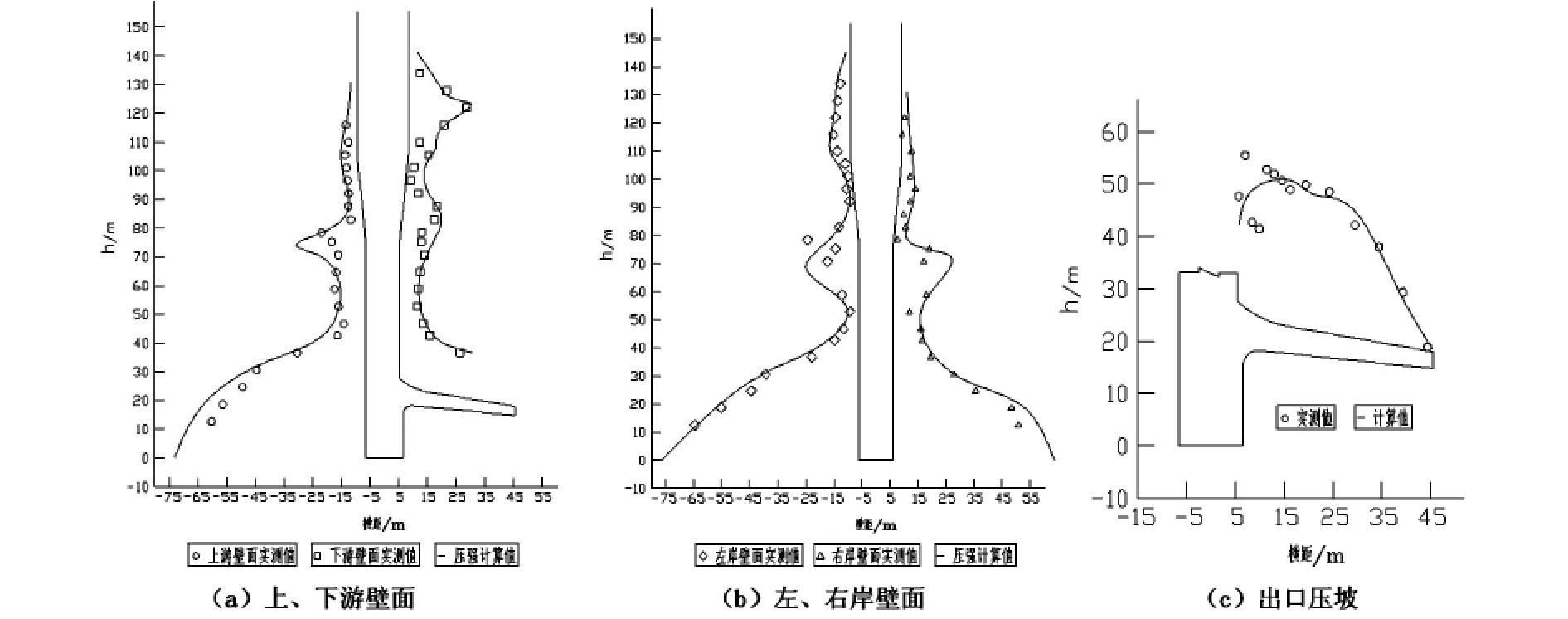
图4 竖井壁面压强分布
水流由竖井壁面非均匀螺旋下泄,到达竖井底部仍有一定旋转速度,这保证了水流与竖井内壁面的良好的贴附,从而尽可能地减小空化空蚀风险;在竖井底部,水流旋转速度较大,环状水跃段(h=34 m~52 m),水流旋转速度较小;随着高程的增加,水流旋转速度有一定增加,在收缩段及涡室段(h=76 m以上区域),水流旋转速度明显大于竖井段的旋转速度。
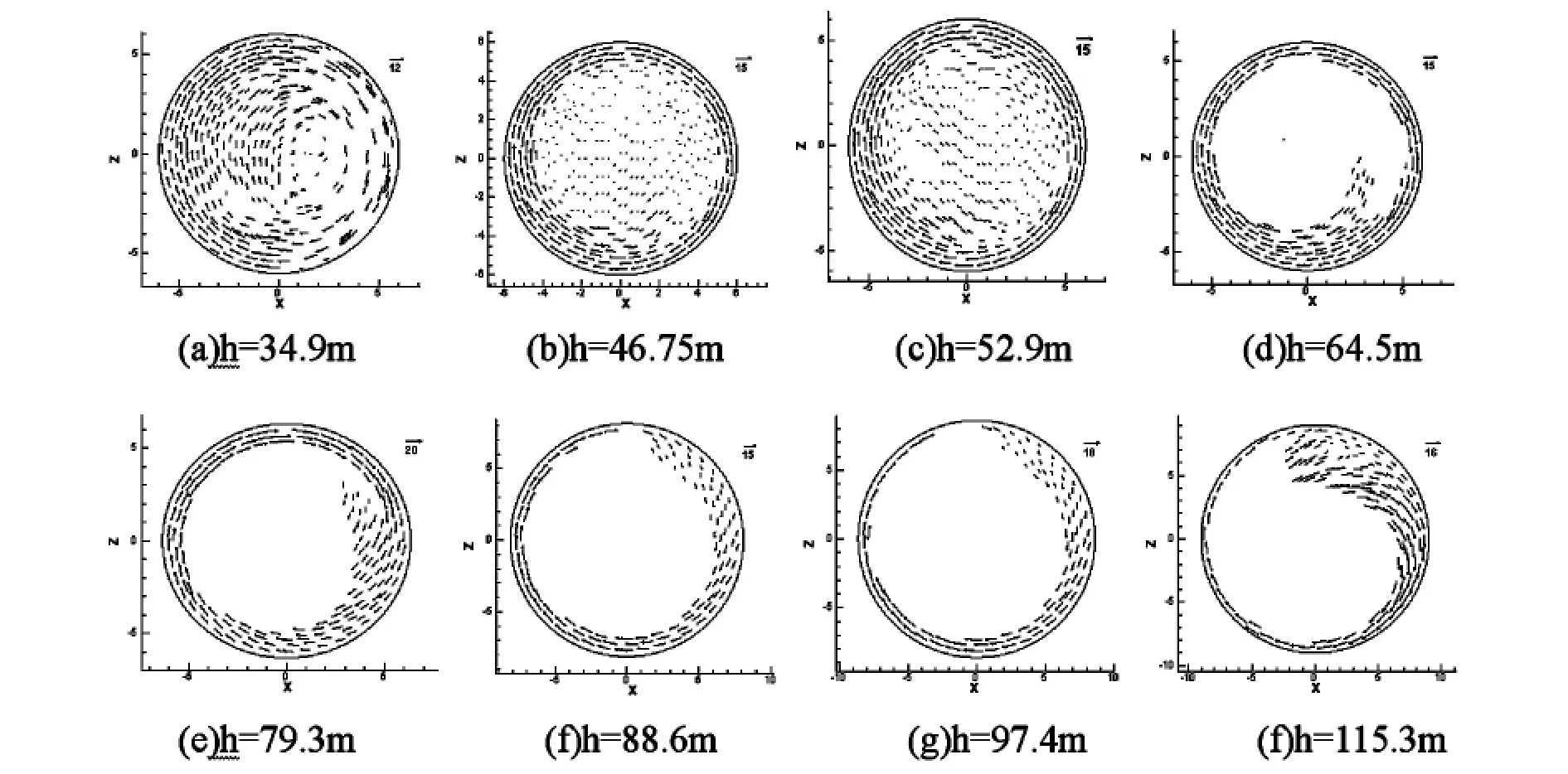
图5 竖井沿程流速分布图
4 结论
通过对旋流竖井内水体的数值计算,将常规水力学参数计算结果与试验结果进行对比分析后发现,数值计算在研究旋流竖井泄洪洞的涡腔形态、沿程水深及壁面压强等方面可以得到与试验研究相一致的结果,因此,可以认为:竖井沿程流速计算值也同样与实验结果具有良好的吻合度,从而有效解决了模型试验难以准确测量流速的问题。
[1] 刘慧卿,张先起.坝内单进口旋流式竖井加洞塞组合消能试验研究.东北水利水电,2003,21:10-12.
[2] 牛争鸣,孙静,程庆迎.竖井进流水平旋转内消能泄水道流速分布与消能率的试验研究[J].水力发电学报,2003,(1):62-69.
[3] 董兴林,高季章,鲁慎吾,等.导流洞改为旋涡式竖井溢洪道综合研究[J].水力发电,1995,22(3):32-37.
[4] 巨江,卫勇,陈念水.公伯峡水电站水平旋流泄洪洞试验研究[J].水力发电学报,2004,23(5):89-91.
[5] 陈华勇,邓军,胡静,谢波,刘斌.竖井旋流泄洪洞洞内流速分布试验研究[J].人民长江,2008,39(12):70-72.
[6] 张晓东,刘之平,高季章,王晓松.竖井旋流式泄洪洞数值模拟[J].水利学报,2003,(8):58-63.
[7] 牛争鸣,程庆迎,谭立新.竖井进流水平旋转内消能泄洪洞流场数值模拟[J].西安理工大学学报,2005,(21):113-117.
[8] 杨朝晖,吴守荣,余挺,贺昌林,邓军,许唯临.竖井旋流泄洪洞三维数值模拟研究[J].四川大学学报(工程科学版),2007,39(2):42-46.
[9] 陈华勇,邓军,胡静,谢波,刘军.旋流式竖井泄洪洞水力要素的数值模拟与试验研究[J].水力发电,2008,34(3):79-82.
[10] 陈大宏,李炜.自由表面流动数值模拟方法的探讨[J].水动力学研究与进展:SerA,2001,16(2):216-224.
[11] Patankar S V.Numerical heat transfer and fluid flow[M].New York:Hemisphere Corporation and Mc Graw Hill Book Company,1980.
TV651.1+3;O242.1
B
1001-2184(2015)05-0162-04
代双键(1987-),男,四川仁寿人,毕业于四川大学水利水电工程设计专业,助理工程师,现为重庆市水利电力建筑勘测设计研究院设计员.
(责任编辑:卓政昌)
2015-09-17

